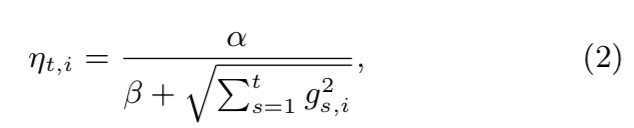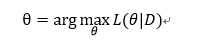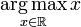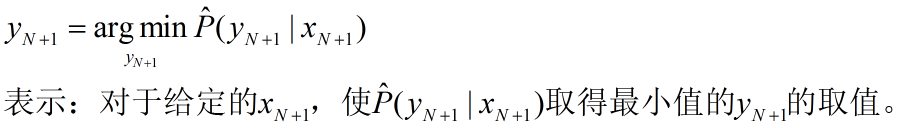FTRL算法是吸取了FOBOS算法和RDA算法的两者优点形成的Online Learning算法。读懂这篇文章,你需要理解LR、SGD、L1正则。
FOBOS算法
前向后向切分(FOBOS,Forward Backward Splitting)是 John Duchi 和 Yoran Singer 提出的。在该算法中,权重的更新分成两个步骤,其中
是迭代次数,
是当前迭代的学习率,
是loss func的梯度,
是正则项,如下:
权重更新的另外一种形式:
对上式argmin部分求导,令导数等于0可得:
这就是权重更新的另外一种形式,可以看到
的更新不仅与
有关,还与自己本身有关,有人猜测这就是前向后向的来源。
L1-FOBOS,正则项为L1范数,其中
:
合并为一步:
令
,将二次项乘开,消去常数项得
闭式解:
推导过程略,思路同下方FTRL闭式解的推导过程。
为什么一般设
?
我们希望这一步更新中,上半步和下半部的步长(学习率)一样。
RDA算法
RDA(Regularized Dual Averaging Algorithm)叫做正则对偶平均算法,特征权重的更新策略如下,只有一步,其中
累积梯度
,
累积梯度平均值
,
是正则项,
是一个严格的凸函数,
是一个关于t的非负递增序列:
L1-RDA:
令
,令
,令
,其中
,
,并且各项同时乘以t,得:
闭式解:
推导过程略,思路同下方FTRL闭式解的推导过程。
L1-FOBOS与L1-RDA对比
从截断方式来看,在 RDA 的算法中,只要梯度的累加平均值小于参数
就直接进行截断,说明 RDA 更容易产生稀疏性;同时,RDA 中截断的条件是考虑梯度的累加平均值,可以避免因为某些维度训练不足而导致截断的问题,这一点与 TG,FOBOS 不一样。通过调节参数
可以在精度和稀疏性上进行权衡。
为什么
是一个严格的凸函数?
因为凸函数+凸函数=凸函数,可以保证整体的凸性,argmin的部分如果不保证凸性,极值就不存在,则无法更新权重。
为什么
是一个关于t的非负递增序列?
可以认为学习率
,
可以看作是学习率的倒数,因为学习率设置为随着迭代次数增加而减小的正数,所以
是一个关于t的非负递增序列。
FTRL算法
FTRL 算法综合考虑了 FOBOS 和 RDA 对于梯度和正则项的优势和不足,其中累积梯度
,
,
,
,
,特征权重的更新公式是:
维度
的学习率设置为
,随着迭代次数增加而减小,
主要作用是保证分母不为0.
使用
替换学习率可将L1-FOBOS、L1-RDA、FTRL写成类似的形式,如下:
各项解释todo
闭式解及其推导过程:
将二次项乘开,消去常数项,得:
设
,则
,得:
对于单个维度
来说:
对上式,假设
是最优解,令上式导数等于0可得:
我们分三种情况进行讨论
当
时:
当
时,满足
,成立
当
时,
且
上式不成立
当
时,
且
上式不成立
当
时:
当
时,不满足
,不成立
当
时,
且
,上式不成立
当
时,
且
,
有解,
当
时:
当
时,不满足
,不成立
当
时,
且
,
有解,
当
时,
且
,上式不成立
综上,可得分段函数形式的闭式解:
论文内的伪代码
引入L2范数与否是等价的
我们不难发现论文[1]中的权重更新公式中是没有L2正则项的,但是伪代码中却有L2正则项系数
,这是因为更新公式中的超参数
,相当于通过调节超参,引入L2范数与否没有区别。论文中的伪代码这样写,相当于减少了一个超参数,如果是调过参的同学就知道减少一个超参数意味着什么。
为什么学习率长这样
类似Adagrad的思想
用硬币实验解释todo
去除正则项的FTRL等价于SGD可推导
论文原话是Without regularization, this algorithm is identical to standard online gradient descent.
如何直观理解累积梯度的作用
在实现上,full train和increment train的有什么区别
FTRL工程实现上的trick
近似代替梯度平方和
如果不理解,回去仔细研究LR的公式。
去除低频特征
由于长尾,大部分特征是稀疏的,且频次很低,online的场景无法用batch的方式去统计特征频次。论文提了两个方案,以泊松概率p决定特征是否更新和建立Bloom Filter Inclusion。我看大部分实现都是用Bloom Filter。
负采样,权重更新时除以负采样率
使用更少的位来进行浮点数编码
四个超参的经验值
如何用FTRL做广告探索todo
[1] McMahan, H. Brendan, et al. "Ad click prediction: a view from the trenches." Proceedings of the 19th ACM SIGKDD international conference on Knowledge discovery and data mining. ACM, 2013.
[2] 张戎 FOLLOW THE REGULARIZED LEADER (FTRL) 算法总结 https://zhuanlan.zhihu.com/p/32903540