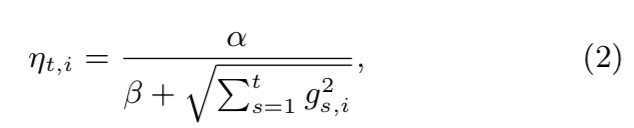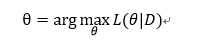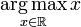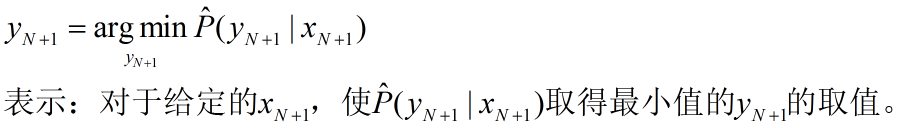概述

GBDT算法是业界比较好用筛选特征的算法，在线学习考虑效率和数据量，经常用GBDT离线筛选特征，输入到在线模型进行实时训练，如今比较好用的方法是GBDT+LR，而FTRL是另外一种很高效的算法，与其类似的有OGD，FOBOS，RDA等，下面将逐一介绍原理以及应用的案例。

线上模型

点击率预估（CTR）问题是计算广告中非常重要的模块，通过预估用户对广告的点击概率来对广告进行排序，进而提升广告效果和收益效率。对于大规模的在线预测模型，不仅要考虑大的数据量带来的处理效率的问题，还要考虑数据的稀疏性对于模型拟合带来的影响。
经典的LR模型主要通过sigmoid函数，将线性拟合结果转化为概率，通过梯度下降（GD）对最大似然概率（loss函数）的求解最终得到参数的估计值。梯度下降法能够保证精度，要想预防过拟合问题一般会加上正则项，L1相对于L2正则能够产生更系数的参数（why？）

在线优化算法

在线学习算法的特点是：每来一个训练样本，就用该样本产生的loss和梯度对模型迭代一次，在线学习算法需要特殊关注模型鲁棒性和稀疏性，由于样本是一个一个到来，参数可能会因为训练样本不足导致过拟合，因此需要算法重点解决模型系数性的问题。对此，业界有以下几种算法从不同角度解决系数问题：

L1正则法

对于L1正则（正则推导），模型权重更新方式为

W t + 1 = W t - η t G t - η t λ s g n (ω t)

$W^{t+1}=W^t-\eta^tG^t-\eta^t\lambda sgn(\omega^t)$
模型稀疏性控制参数

λ λ $\lambda$ 会将接近0的参数趋近于0

简单截断法

相对于L1正则，属于简单粗暴的方法，直接将不满足阈值的系数设置为0,。以k为窗口，如果t/k不为整数时，采用标准的SGD进行优化，否则采用如下方法：

W t + 1 = T 0 (W t - η t G t, θ) T 0 (v i, θ) = {0, i f ｜ v i ｜ \leq θ v i, o t h e r s

$W^{t+1}=T_0(W^t-\eta^tG^t,\theta)\\ T_0(v_i,\theta)=\begin{cases} 0,　　if　｜v_i｜\leq \theta\\v_i,　　others \end{cases}$
通过参数

θ θ $\theta$ 控制模型稀疏性（ define）

梯度截断法TG

在简单截断法的基础上提出了改进：

W t + 1 = T 1 (W t - η t G t, η t λ t, θ) T 1 (v i, α, θ) = ⎧ ⎩ ⎨ m a x (0, v i - α), i f ｜ v i ｜ \in [0, θ] m i n (0, v i + α), i f ｜ v i ｜ \in [- θ, 0] v i, o t h e r s

$W^{t+1}=T_1(W^t-\eta^tG^t,\eta^t\lambda ^t,\theta)\\ T_1(v_i,\alpha,\theta)=\begin{cases} max(0,v_i-\alpha),　　if　｜v_i｜\in [0,\theta]\\min(0,v_i+\alpha),　　if　｜v_i｜\in [-\theta,0]\\v_i,　　others \end{cases}$
参数

λ λ $\lambda$ 和

θ θ $\theta$ 控制模型稀疏，值越大越稀疏，写入为简单截断法与TG的区别

在线梯度下降OGD（Online gradient descent）

线下GDs

GD算法：

SGD算法：

与SGD比较，GD需要每次扫描所有的样本以计算一个全局梯度，SGD则随机抽几个数据进行训练，通常SGD可以更快的逼近最优值，效率会高很多

线上GD

OGD：

online learning强调学习的实时性，流式的，每次训练不用全部样本，而是根据训练好的模型，每来一个样本更新一次模型，这种方法叫做OGD（Online Gradient Descent）
目标函数：

m i n w = 1 T \sum t = 1 T f (w, z t) + ψ (w)

$min_w =\frac{1}{T}\sum_{t=1}^Tf(w,z_t)+\psi(w)$
其中使用了混合正则化项：

ψ(w)=λ||w||1+(σ/2)||w||22 ψ ( w ) = λ | | w | | 1 + ( σ / 2 ) | | w | | 2 2 $\psi(w)=\lambda ||w||_1+(\sigma /2)||w||_2^2$

我们将online learning中的累计损失记为 $\sum_{t=1}^Tl_t(h_t)$ ，如果挑选 $h_t$ 的策略集H是凸的，而且随时函数 $l_t(h_t)$ 关于 $h_t$ 是凸的，那么我们称这个问题为OCP（Oline Convex Optimization）。通常我们将 $h_t$ 表示为一个向量。

在线梯度下降算法在t时刻做两步操作：

利用当前得到数据对 $h_t$ 进行一次梯度下降得到 $h_{t+1}$
投影操作：
- 如果新的 $h_{t+1}$ 在H中，则将其投影：
  
  $h t + 1 = \prod H (h t - η t \nabla l t (h t))$ $h_{t+1}=\prod_H(h_t-\eta_t\nabla l_t(h_t))$
  其中 $\nabla l_t(h_t)$ 是 $l_t(h_t)$ 关于 $h_t$ 的导数， $\eta _t$ 是学习率， $\prod _H(.)$ 是投影子，公式为 $\prod _H(x)=arg min_{y \in H}||x-y||$ ，表示向量x投影成与x最近的但在H中的向量。因此算法的目的在于通过投影寻找最优的 $h_t$
- 否则不做任何处理

在线梯度下降只知道当前一个数据所得到的有偏差的梯度，能保证减少 $l_t(h_t)$ ，对别的项的减少程度是未知的，可能会走点弯路。其优势在于每步是需要看一下当前的一个数据，代价很小。

论文：http://www0.cs.ucl.ac.uk/staff/M.Pontil/reading/lsqonline280406.pdf

AOGD：

具体推导见论文：https://papers.nips.cc/paper/3319-adaptive-online-gradient-descent.pdf

FOBOS（Forward-Backward Splitting）

FOBOS称为前后项算法，其权重的更新方式分为两个部分：

第一步为标准的梯度下降，然后将结果进行正则化的微调，满足最速下降切保证了一定的稀疏性。其中 $\psi (W)$ 是正则项可以对权重进行约束，常用的选择为L1，则对应的方法为L1-FOBOS

RDA

RDA（正则对偶平均）是微软的研究成果，其权重更新策略为：

权重更新包括三部分，一部分是线性加权，即对历史梯度进行加权平均；第二部分正则项部分对特征进行稀疏化；第三部分严格递增序列相当于额外的正则项。实验证明可以产生较好的稀疏和精度

FTRL（Follow-the-regularized-Leader）

FTRL是Google提出的在线算法，由于其在工程实现上进行了大量优化，在工业界应用非常广泛。主要思想概述如下图：

算法流程：

FTRL的权重更新策略为：

$g_{1:t}=\sum_{s-1}^tg_t$ 相当于新产生的权重验证所有样本的梯度并且和历史权重不偏离太远，通过L1正则进行稀疏性约束。这样既保证了权重更新的精度又保证了稀疏性。
参数 $\sigma_s$ 是一个和学习率相关的参数 $\sum_{s-1}^t\sigma_s=\frac{1}{\eta_t}$ ， $\eta_t=\frac{1}{\sqrt{t}}$ 是非增序列
公式推导

工程优化：
1. 预测的内存方面：L1范式加策略，训练结果w很稀疏，在用w做predict的时候节省了内存，很直观
2. 训练的内存方面：
1）在线丢弃训练数据中很少出现的特征，即稀疏特征处理：

Possion Inclusion(通过一定概率扔掉特征，对某一维度特征所来的训练样本，以p的概率接受并更新模型)
BloomFilter Iclusion(通过碰撞优化特征，用bloom filter从概率上做某一特征出现k次才更新)

2）浮点数重新编码

特征权重不需要用32bit或64bit的浮点数存储，存储浪费空间
16bit encoding，但是要注意处理rounding技术对regret带来的影响

3）训练若干相似model

对同一份数据序列，同时训练多个相似的model
这些model有各自独享的一些feature，也有一些共享的feature
出发点：有的特征维度可以是各个模型独享的，而有的各个模型共享的特征，可以用同样的数据训练

4）Single Value Structure（据说有公司已经在实际中这么搞，大数据量下也能够保证不错的auc）

多个model公用一个feature存储（例如放到cbase或redis中），各个model都更新这个共有的feature结构
对于某一个model，对于他所训练的特征向量的某一维，直接计算一个迭代结果并与旧值做一个平均

5）使用正负样本的数目来计算梯度的和（所有的model具有同样的N和P）

\sum g 2 t, i = \sum p o s i t i v e e v e n t s (1 - p t) 2 + \sum n e g a t i v e e v e n t s p 2 t \approx P (1 - P N + P) 2 + N (P N + P) 2 = P N N + P

$\sum g_{t,i}^2=\sum_{positive events}(1-p_t)^2+\sum_{negative events}p_t^2\\\approx P(1-\frac{P}{N+P})^2+N(\frac{P}{N+P})^2\\ =\frac{PN}{N+P}$

６) Subsampling Training Data

在实际中，CTR远小于50%，所以正样本更加有价值。通过对训练数据集进行subsampling，可以大大减小训练数据集的大小
正样本全部采（至少有一个广告被点击的query数据），负样本使用一个比例r采样（完全没有广告被点击的query数据）。但是直接在这种采样上进行训练，会导致比较大的biased prediction
解决办法：训练的时候，对样本再乘一个权重。权重直接乘到loss上面，从而梯度也会乘以这个权重。
$w t = {1 e v e n t t i s i n a c l i c k e d q u e r y 1 r e v e n t t i s i n a q u e r y w i t h n o c l i c k s$ $w_t=\begin{cases} 1　event t is in a clicked query\\ \frac{1}{r}　event t is in a query with no clicks\\ \end{cases}$

应用：https://www.cnblogs.com/arachis/p/FTRL.html

算法对比：

不同的方法按照统一的描述形式，区别点主要在第二项和第三项：
- 第一项：梯度或累积梯度
- 第二项：L1正则化项的处理
- 第三项：这个累积家和限定了新的迭代结果x不要离已迭代过的解太远或者离0（center）太远，这一项其实也是low regret的需求

参考：
1. Ad Click Prediction: a View from the Trenches(2013)
2. https://blog.csdn.net/fangqingan_java/article/details/51020653
3. https://blog.csdn.net/fangqingan_java/article/details/48951191
4. https://blog.csdn.net/guohecang/article/details/52388970
5. https://wenku.baidu.com/view/e70abd03551810a6f52486eb.html
6. https://blog.csdn.net/Losteng/article/details/51119764