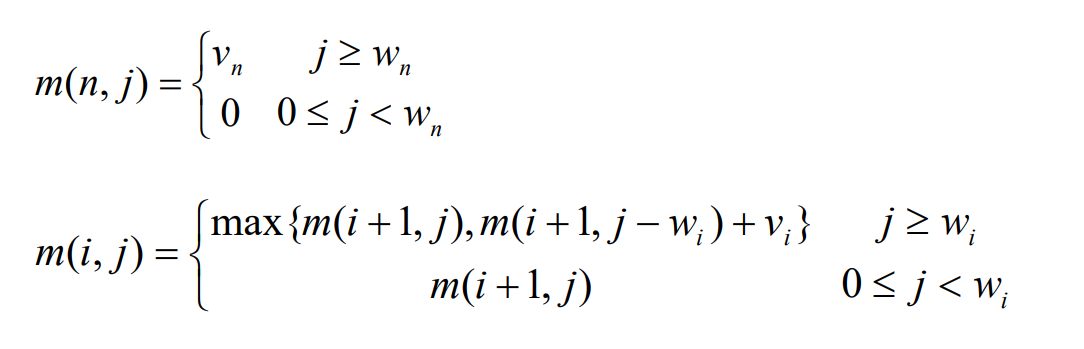二维dp数组01背包

1. 确定dp数组以及下标的含义

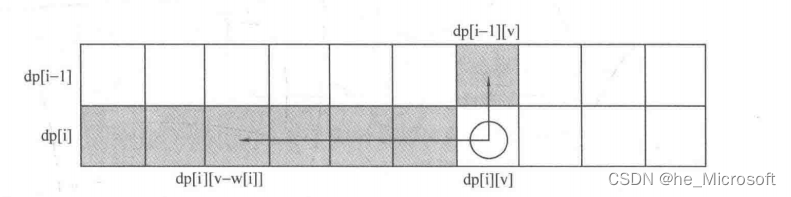
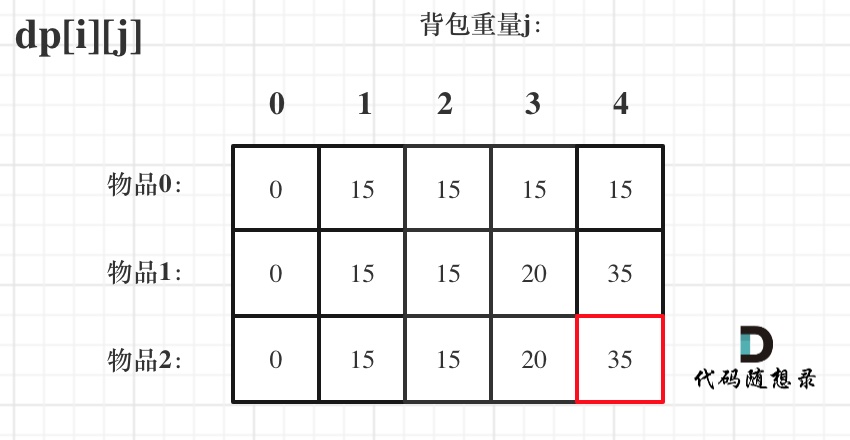
 使用二维数组，即dp[i][j] 表示从下标为[0-i]的物品里任意取，放进容量为j的背包，价值总和最大是多少

      2.递推公式：dp[i][j]=dp[i-1][j-weight]+value[i]   dp[i][j]=dp[i-1][j]

     3.数组初始化：dp[100][100]={0};

for(j=BagSize;j>=weight[0];j--)//第一个物品重量{//dp[0][j]=dp[0][j - weight[0]]+value[0];//第一列都为一个数dp[0][j]=value[0];//第一个物品的价值}

    4.遍历数组：

for(j=1;j<i;j++)//遍历物品for(k=0;k<=BagSize;k++)//遍历背包重量{if(k<weight[j])dp[j][k]=dp[j-1][k];elseif(dp[j-1][k-weight[j]]+value[j]>dp[j-1][k])dp[j][k]=dp[j-1][k-weight[j]]+value[j];elsedp[j][k]=dp[j-1][k];//当k=weight[j]时dp[j-1][k-weight[j]]==0}

  5.打印数组 

for ( j= 0; j < i; j++) {for ( k = 0; k <=BagSize; k++){printf("%d  ",dp[j][k]);}printf("\n");}

 6.总代码

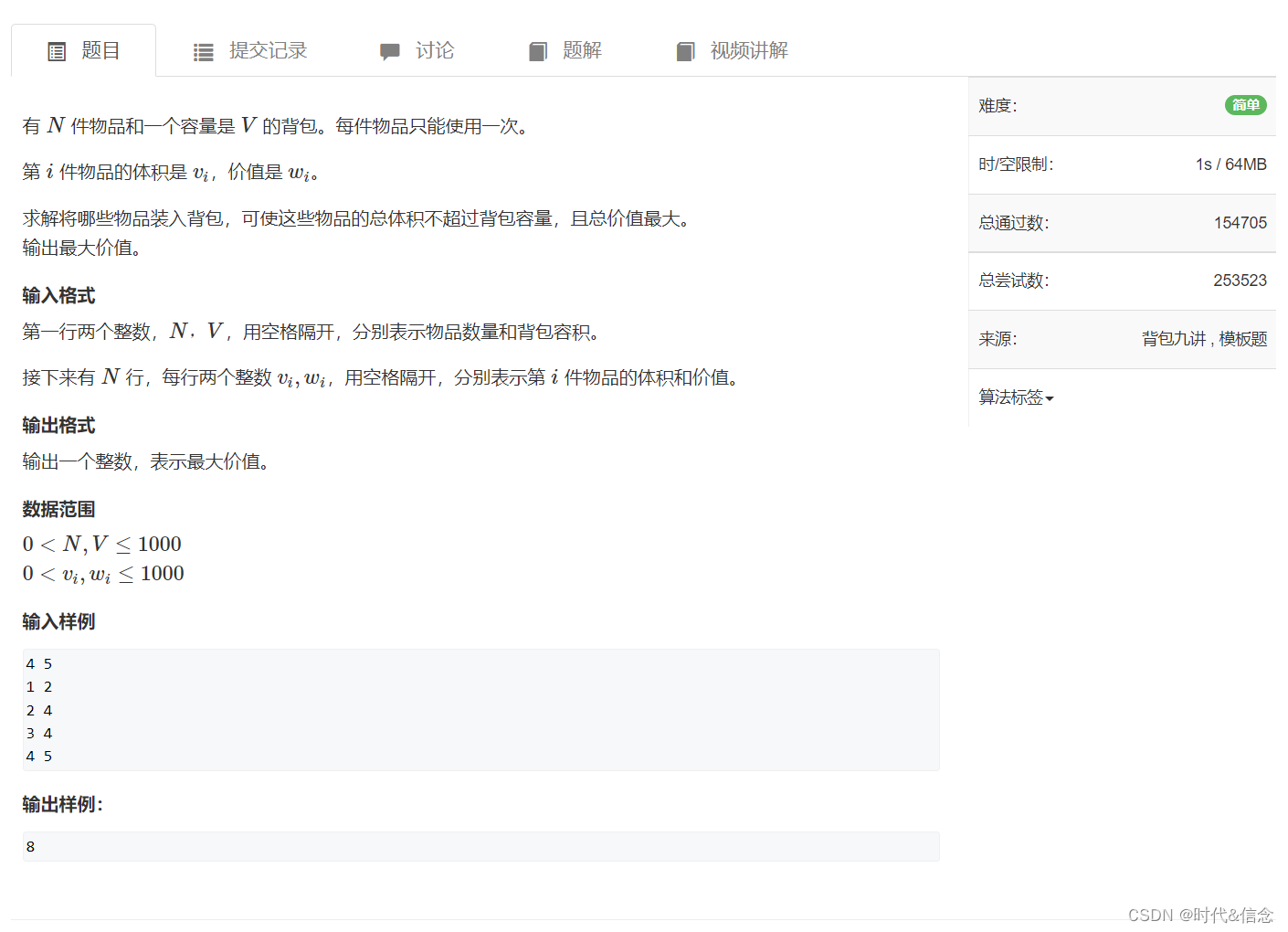
/*01 背包
有N件物品和一个最多能被重量为W 的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。
每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。*/#include<stdio.h>
int main()
{   //dp[i][j]是物品放入任意容量为j的背包中的最大价值int BagSize,weight[100],value[100],dp[100][100]={0};int i=0,j,k,t,m;scanf("%d",&BagSize);while(scanf("%d %d",&weight[i],&value[i])!=EOF){i++;}//初始化for(j=BagSize;j>=weight[0];j--)//第一个物品重量{//dp[0][j]=dp[0][j - weight[0]]+value[0];//第一列都为一个数dp[0][j]=value[0];//第一个物品的价值}//dp[i][0]=0;/*for(j=1;j<5;j++){dp[0][j]=15;}*///遍历数组for(j=1;j<i;j++)//遍历物品for(k=0;k<=BagSize;k++)//遍历背包重量{if(k<weight[j])dp[j][k]=dp[j-1][k];elseif(dp[j-1][k-weight[j]]+value[j]>dp[j-1][k])dp[j][k]=dp[j-1][k-weight[j]]+value[j];elsedp[j][k]=dp[j-1][k];//当k=weight[j]时dp[j-1][k-weight[j]]==0}printf("%d",dp[i-1][BagSize]);printf("\n");//动态规划表的输出for ( j= 0; j < i; j++) {for ( k = 0; k <=BagSize; k++){printf("%d  ",dp[j][k]);}printf("\n");}return 0;
}

​​​​​​​