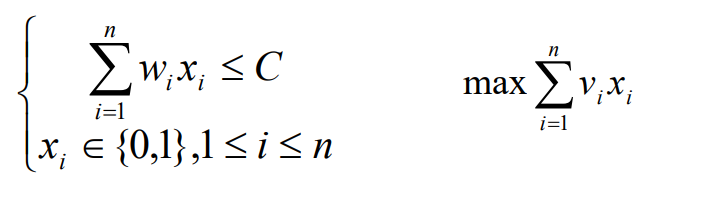👨‍🎓作者简介：一位喜欢写作，计科专业大二菜鸟

🏡个人主页：starry陆离

🕒首发日期：2022年5月16日星期一

🌌上期文章：【动态规划】最长上升子序列

📚订阅专栏：算法分析与设计
如果文章有帮到你的话记得点赞👍+收藏💗支持一下哦

---

1. 问题描述

给定n种物品（每种物品只有一件）和一个背包：物品i的重量是wi，其价值 为vi，背包的容量为C。问应如何选择装入背包的物品，使得装入背包中物 品的总价值最大?

对于每种物品，只有两种选择：装(1)或者不装(0)，不允许装物品的一部分

因此有这么一个著名的公式：

找出物品选择的组合的重量总和要不大于背包的容量为C，且要找出这些组合中装入背包中物品的总价值的最大的组合

2. 问题分析

如果穷举这些组合，我们知道每一个物品都有选和不选，则一共有2 ⁿ(n是物品的种类)；然后去除这些组合中大于背包的容量为C的组合，再找总价值最大的即为解；显然这个数量级太大了

2.1 减少规模

定义m(i，j)是背包容量为j，可选择物品为i，i+1，…，n时0-1背包问题的最优值

则m(i+1，j)为可选择物品为i+1，…，n时0-1背包问题的最优值

。。。依次类推

m(n,j)为可选择物品为n时0-1背包问题的最优值，此时，规模已为1

即当可选物品为n时，背包容量为j，如果此时的背包容量能装下第n个物品，那么m(n,j)的最优值就是第n个物品的价值v_n，装不下那就是0；（因为现在的可选物品只有第n个）

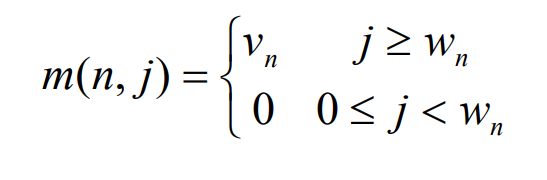
2.2 推导递归式

判断是否放入第i件？

1）不放，背包当前产生价值仍为m(i+1，j)

2）放入，调整背包容量j-w_i，背包当前产生价值为m(i+1, j-w_i)+v_i

结合两式即可得：

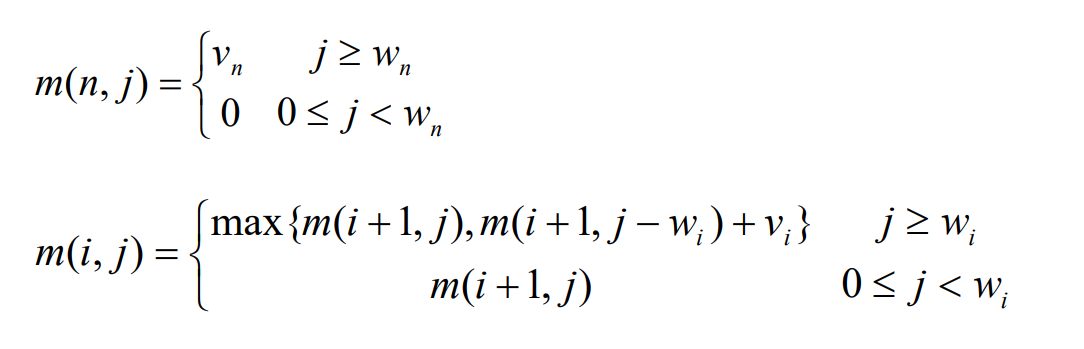
3 填DP表

已知n=5, c=10, w={2, 2, 6, 5, 4}, v={6, 3, 5, 4, 6}

绘制m[i,j]的最下面两行

思路：

• 由上面的分析可知，我们是从下往上，从左往右填dp表，

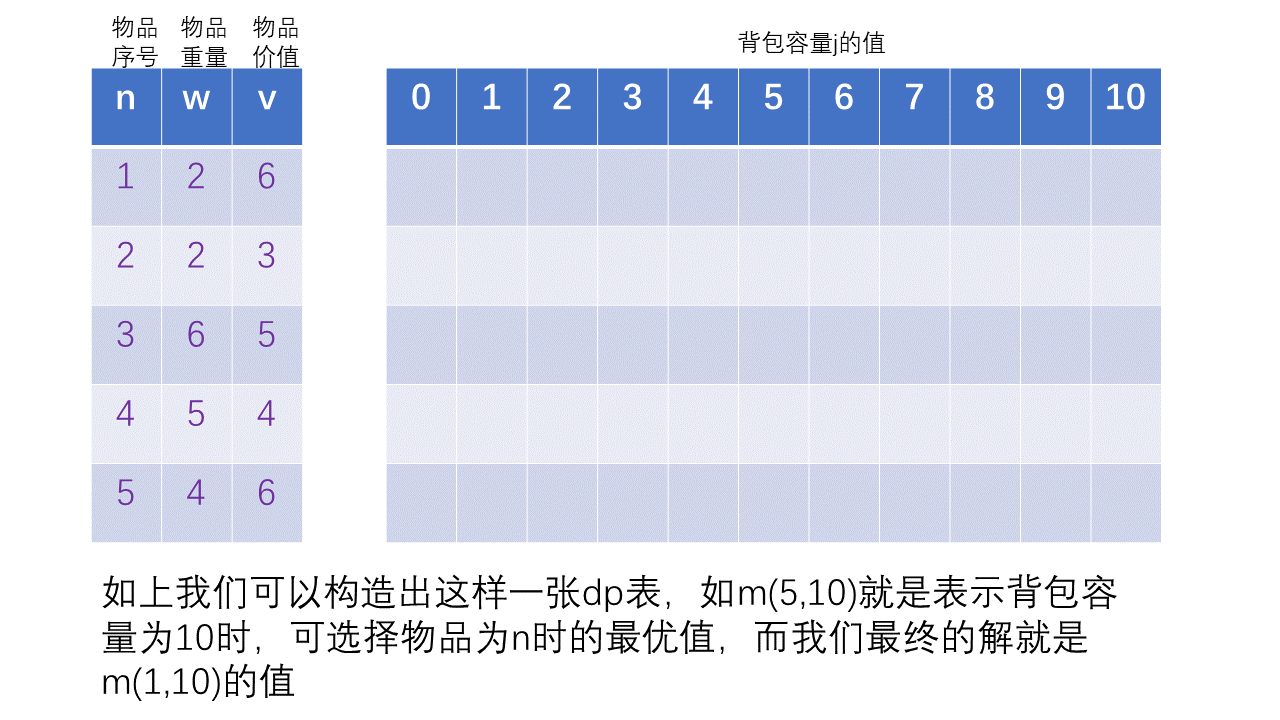
• 如m(5,10)就是表示背包容量为10时，可选择物品为n时的最优值，而我们最终的解就是m(1,10)的值

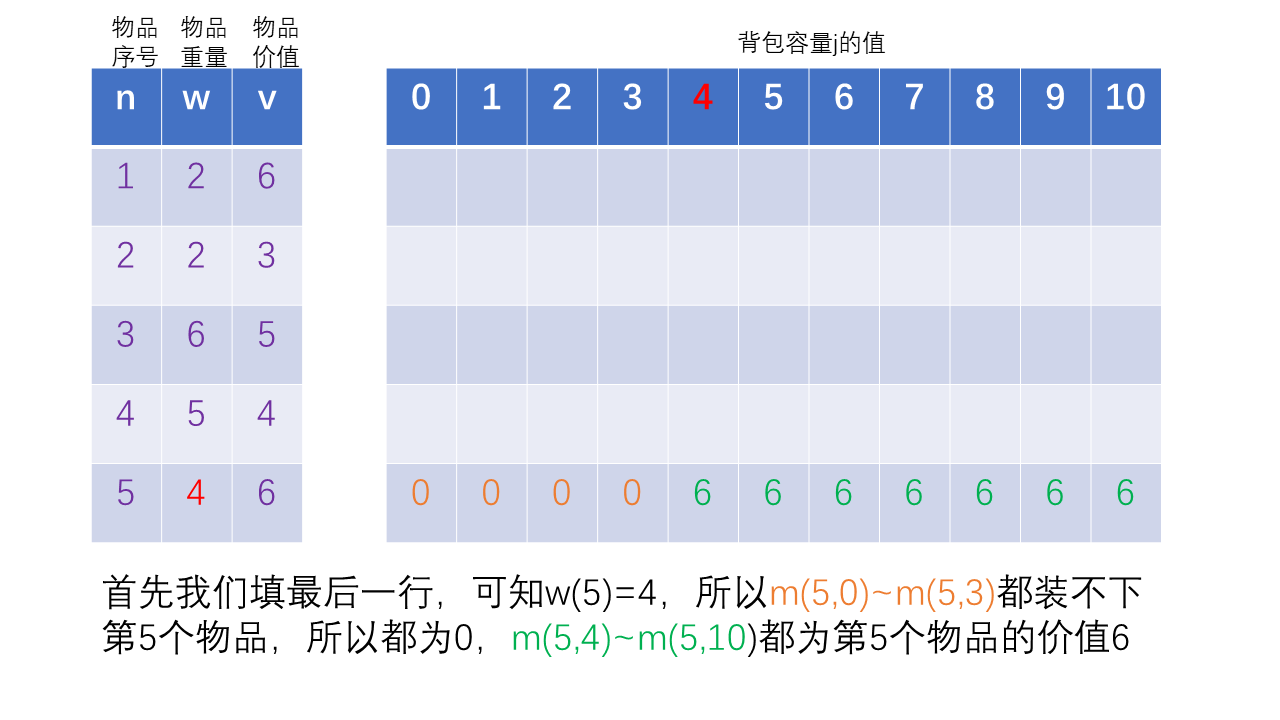
• 首先由第一个公式填最后一行m(5,j)(0<=j<10)

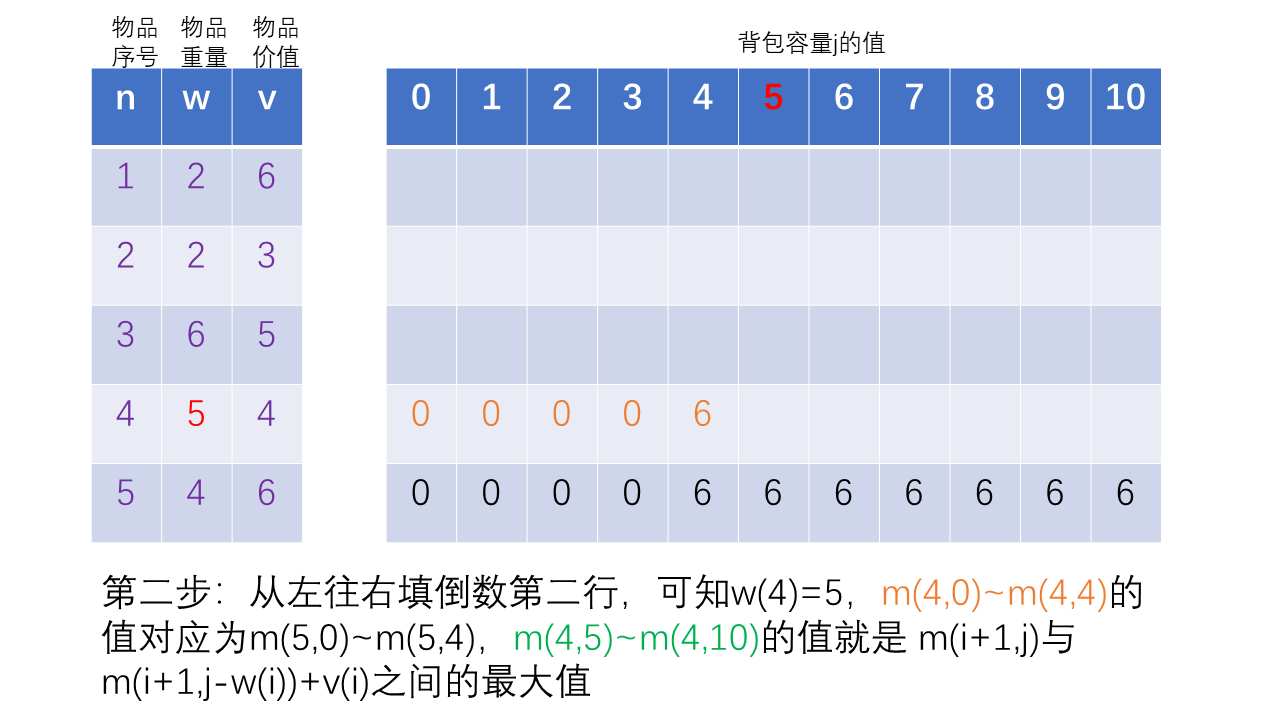
• 然后有第二个公式填剩下的表格

4 图解算法

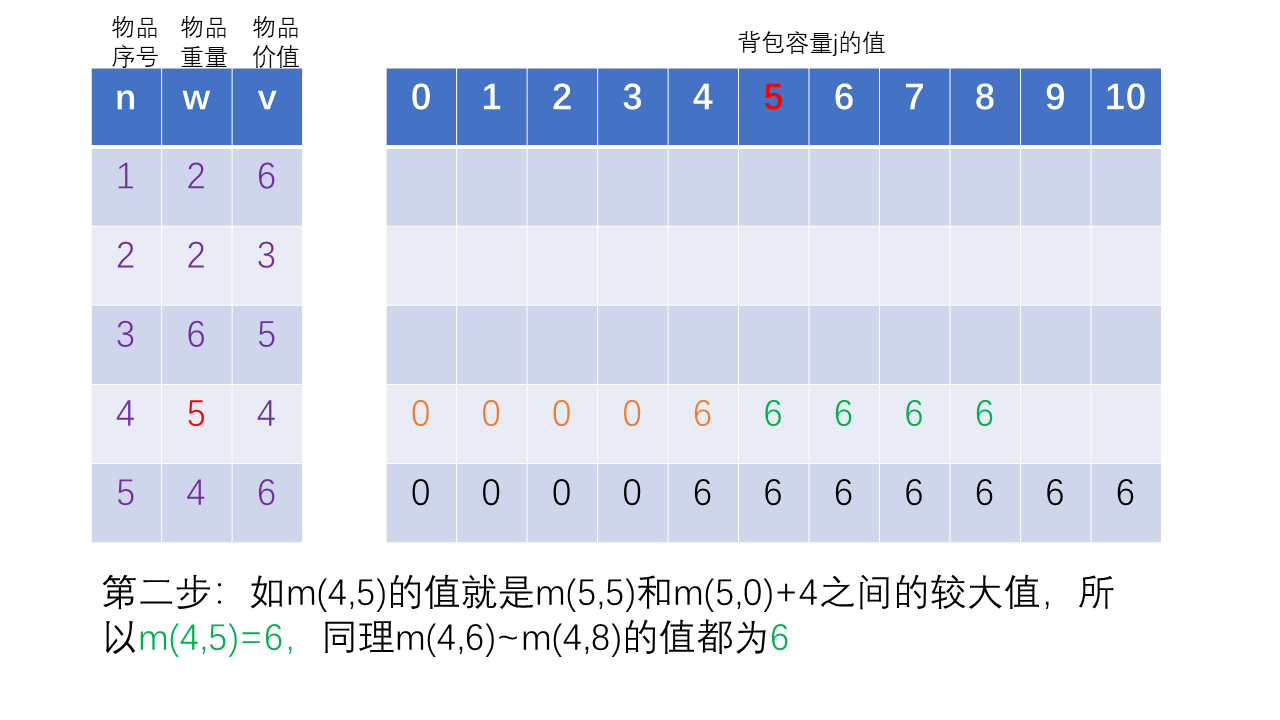
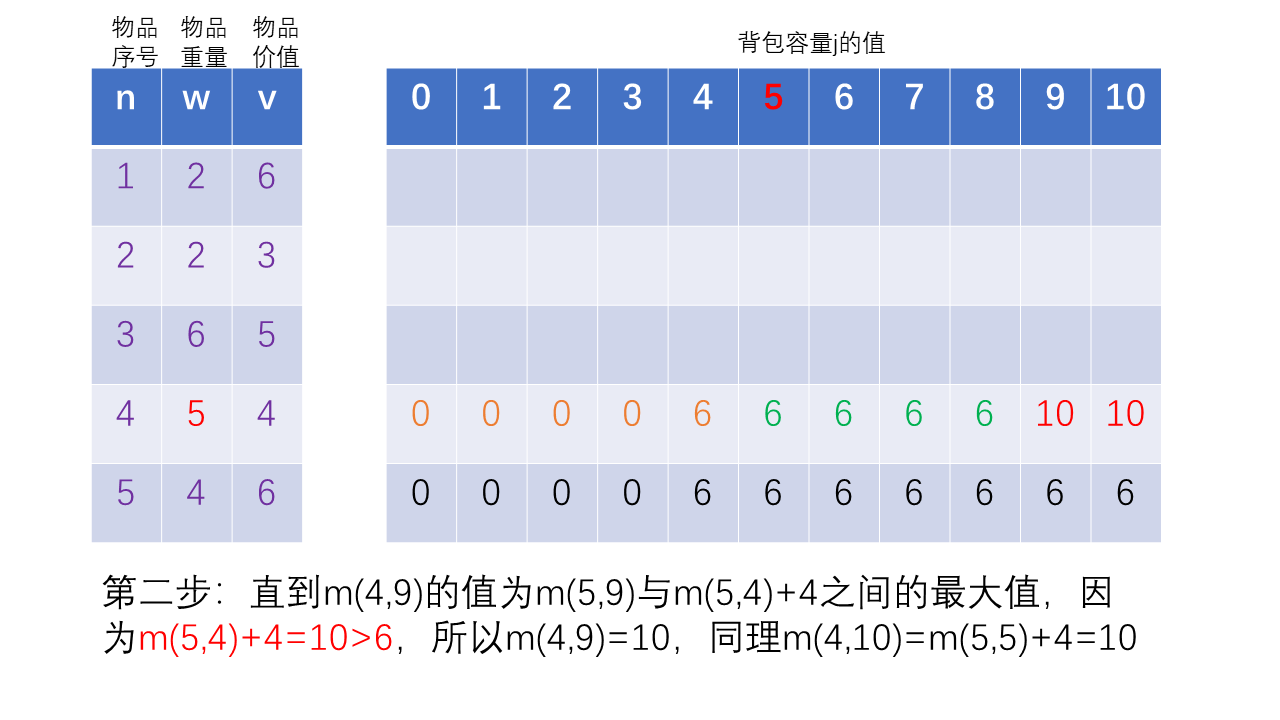
​ 剩下的两行也是用同样的方法递推，读者可自己完成，理解这个逻辑过程

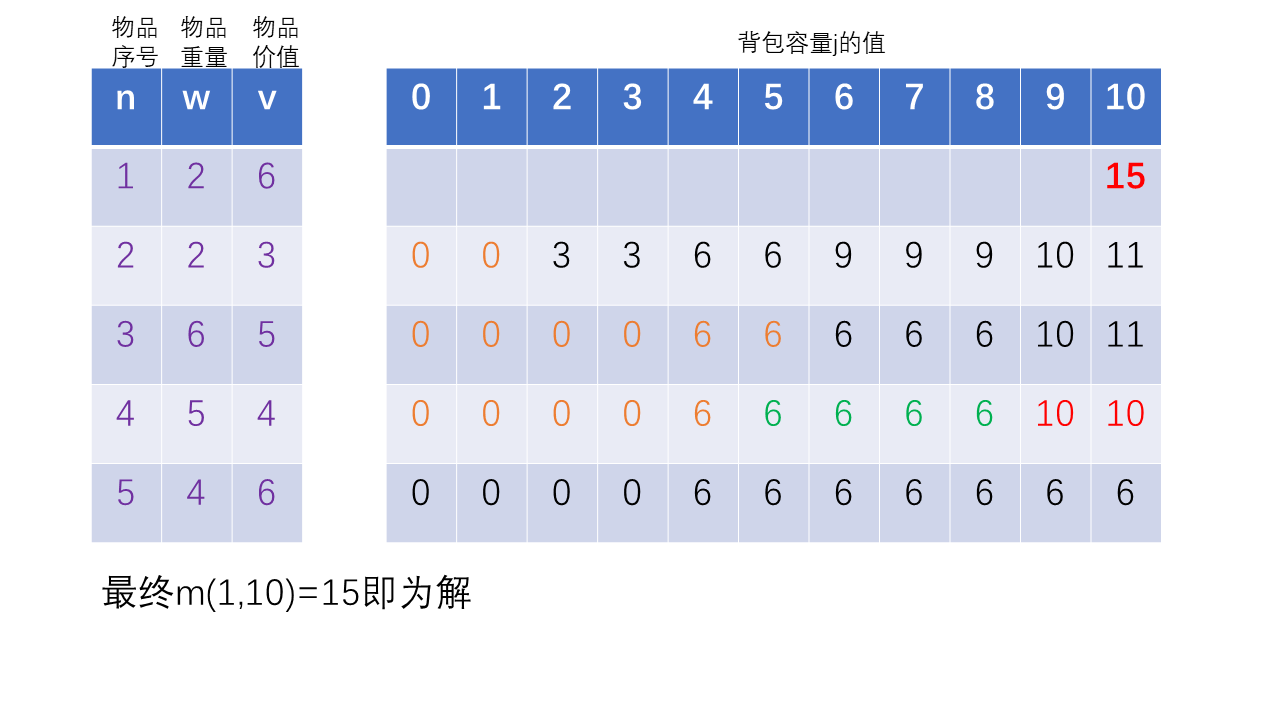
5 代码实现

时间复杂度：O（nc)(n是物品种类，c是背包容量)

空间复杂度：S（nc)

private static int DpSolve(int n, int c, int[] w, int[] v, int[][] dp) {//初始化第n行for(int j=0;j<=c;++j) {if(j>=w[n]) {//System.out.println("w[n]="+w[n]);dp[n][j]=v[n];}}//动态规划for(int i=n-1;i>=1;i--) {for(int j=1;j<=c;++j) {if(j<w[i]) {dp[i][j]=dp[i+1][j];}else {dp[i][j]=Math.max(dp[i+1][j], dp[i+1][j-w[i]]+v[i]);}}}return dp[1][c];}

6. 构造最优解

能够求出01背包问题的最优值，我们如何求出一个最优解呢？

如上面的问题的最优解为1-》2-》5，如果用1代表选择物品，0代表不选择，那么结果可表示为11001

这个结果是如何得出的呢？

1. 只需要当前的m(i,j)和它的下面的最优值m(i+1,j)比较，
   • 如果两者相等说明没有选择物品i，因为价值没有增加
   • 如果两者不相等说明选择了物品i，则需要把当前的背包容量j减去物品i的重量w(i)，得出m(i+1,j-w(i))，其意义在于找到装入物品i前的背包能取得的最优值；
2. 同理依次类推，循环执行第一步，直到找到倒数第二个物品是否选择
3. 最后一步单独判断最后一个物品有没有选择，如果m(n,j)==0则表示没选择最后一个，不为0说明选择了

如上面的问题的最优解为1-》2-》5，如果用1代表选择物品，0代表不选择，那么结果可表示为11001

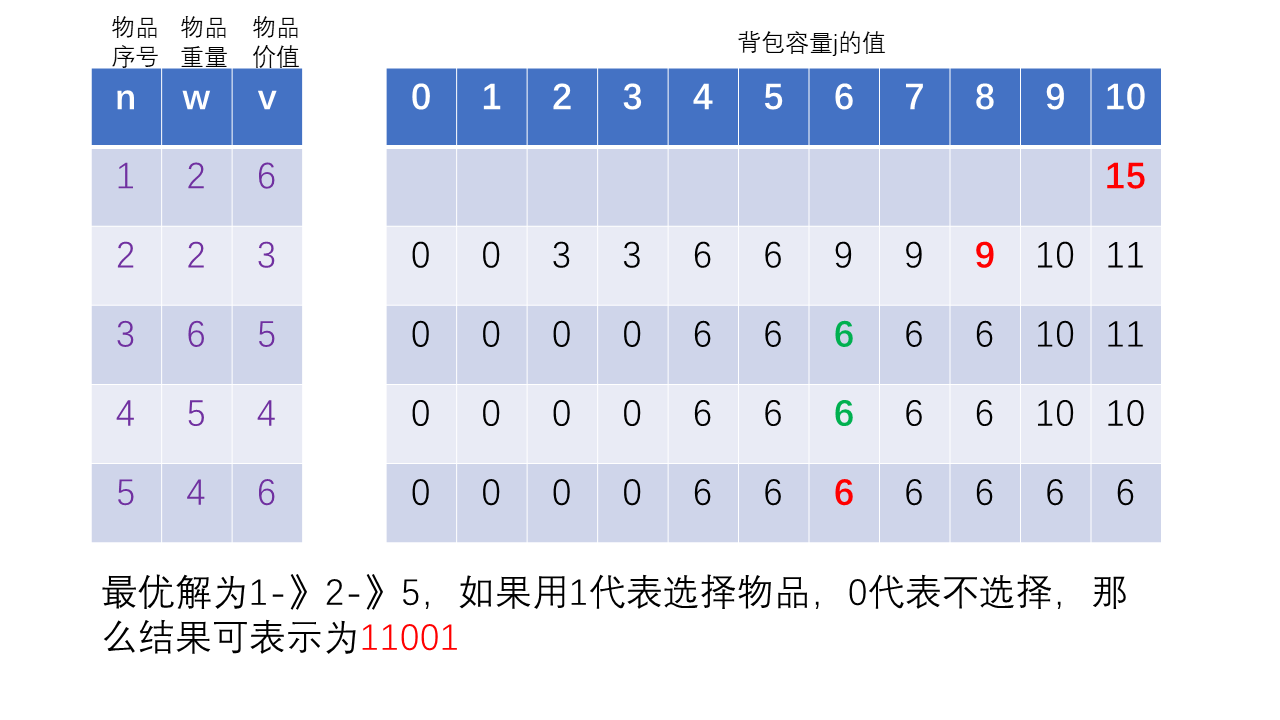
只需要当前的m(i,j)和它的下面的最优值m(i+1,j)比较，

• 如果两者相等说明没有选择物品i，因为价值没有增加；

• 如果两者不相等说明选择了物品i，则需要把当前的背包容量j减去物品i的重量w(i)，得出m(i+1,j-w(i))，其意义在于找到装入物品i前的背包能取得的最优值；

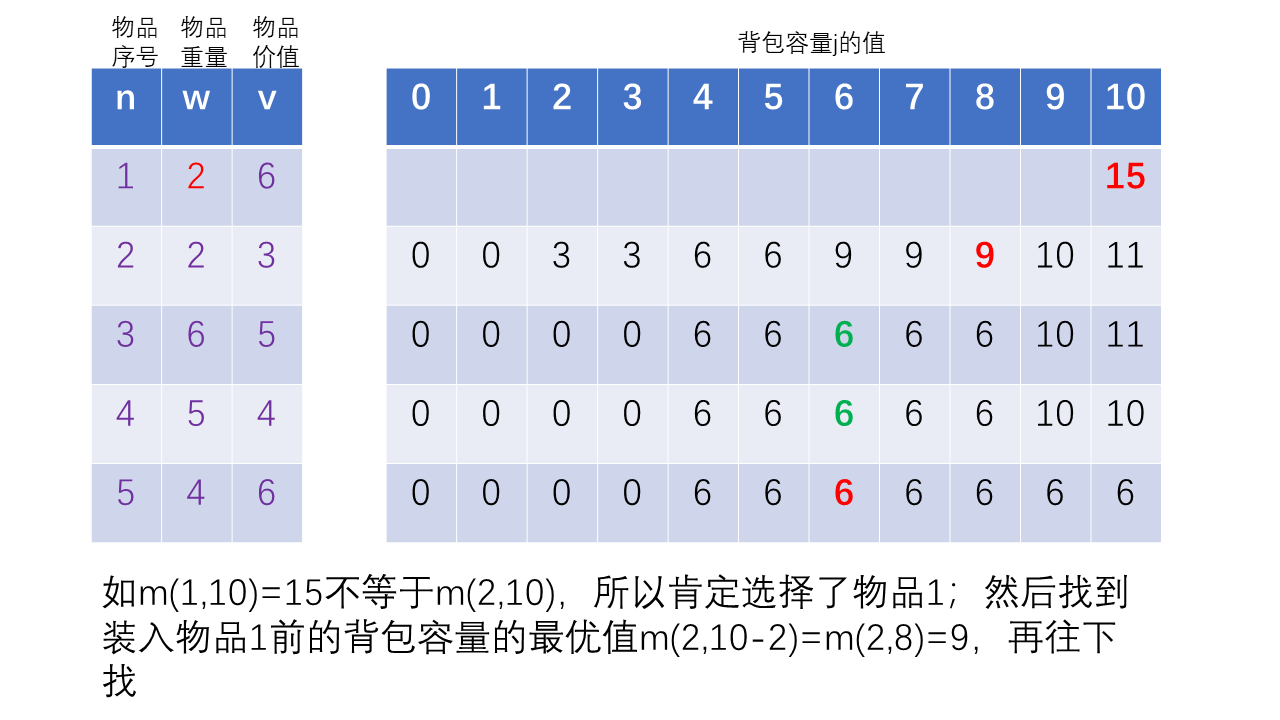
​ 同理依次类推，循环执行第一步，直到找到倒数第二个物品是否选择

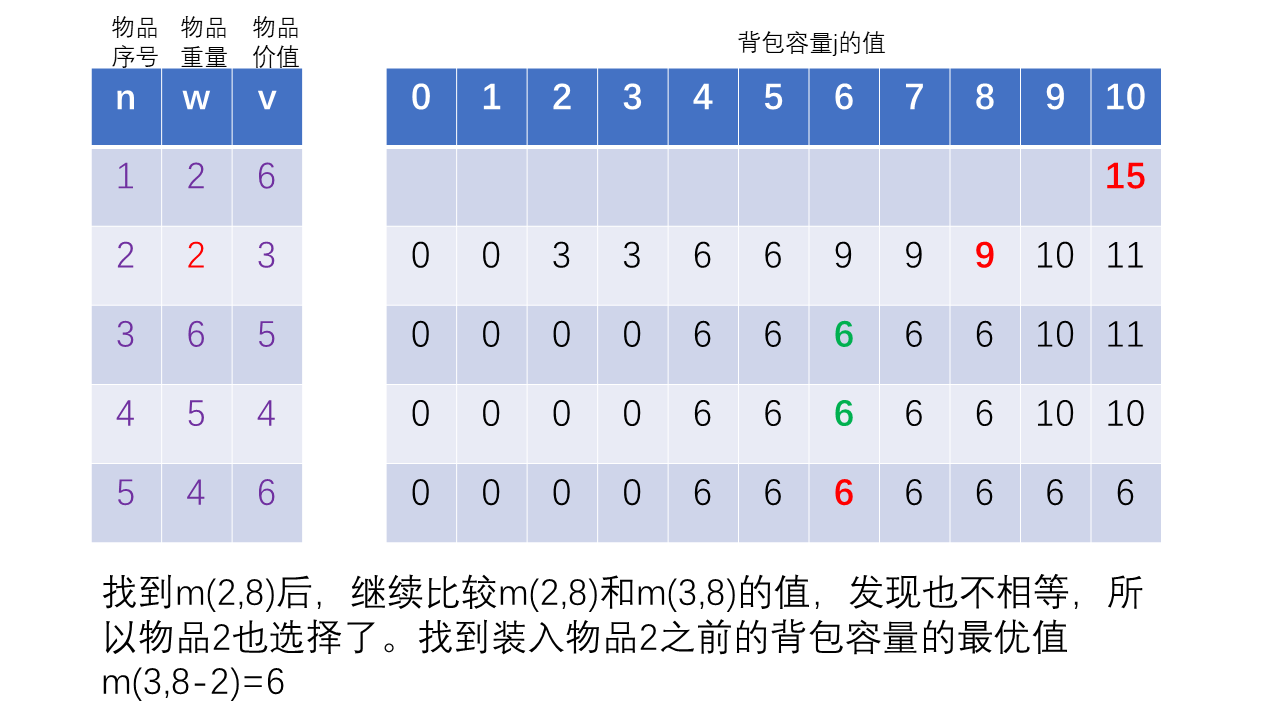
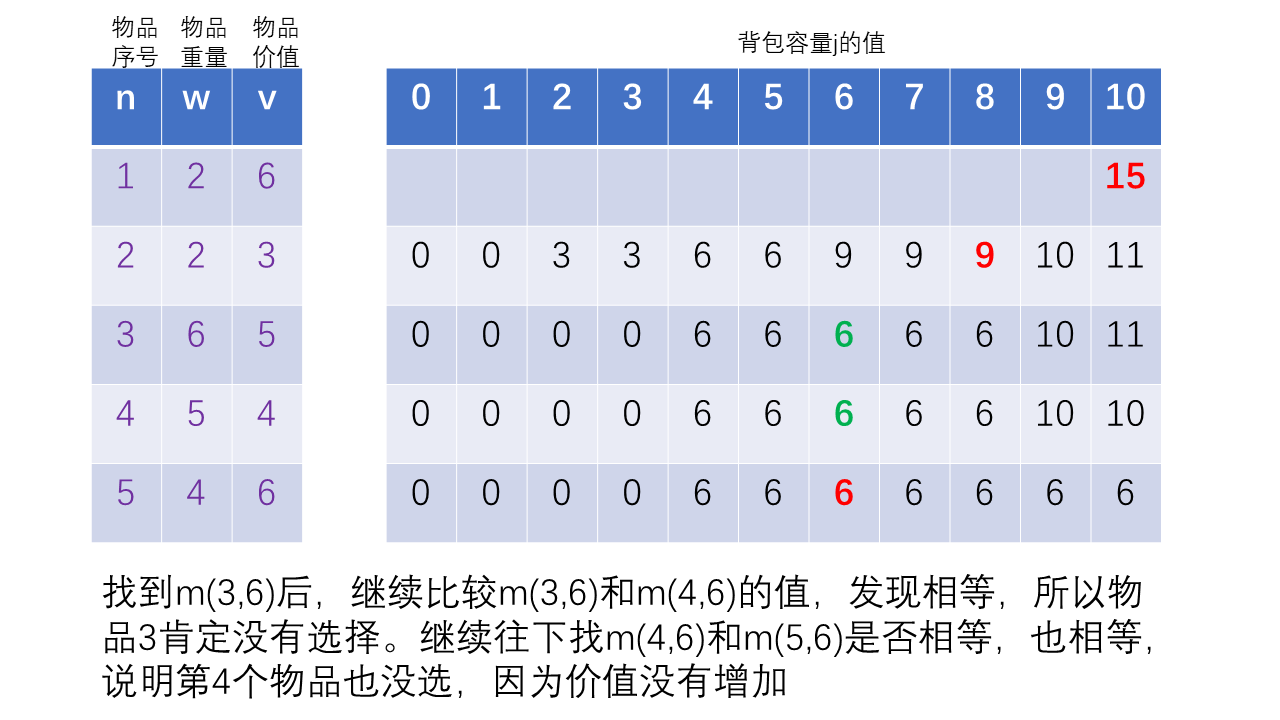
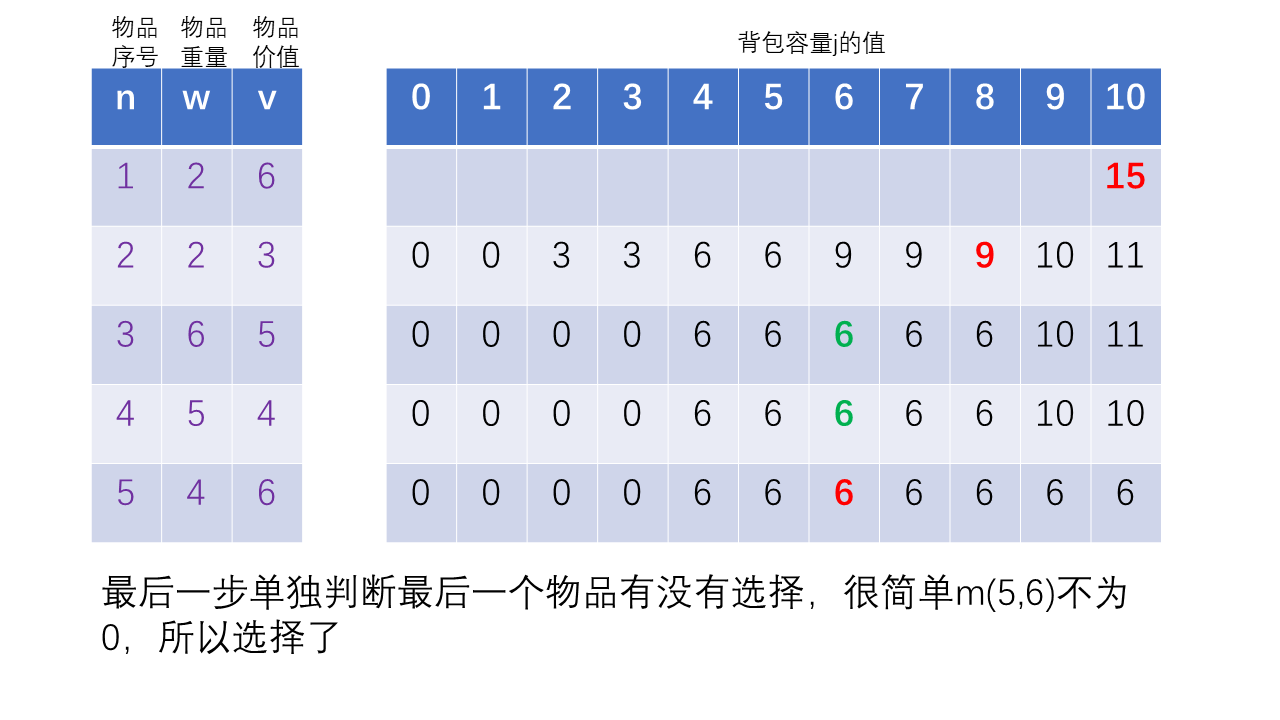
​ 最后一步单独判断最后一个物品有没有选择，如果m(n,j)==0则表示没选择最后一个，不为0说明选择了

private static void Gouzao(int n, int c, int[] w, int[] v, int[][] dp) {for(int i=1;i<n;++i) {if(dp[i][c]==dp[i+1][c]) {//相等说明没选，输出0System.out.print("0");}else {//不相等说明选择了，输出1System.out.print("1");//更新背包的容量，要减去第i个物品的重量//准备去找装入物品i前的背包能取得的最优值c=c-w[i];}}//处理最后一个物品int last=(dp[n][c]>0?1:0);System.out.println(last);}

7. 练习题

原题地址：https://acm.hnucm.edu.cn/JudgeOnline/

题目描述

给定n种物品和一个背包，物品i的重量是Wi，其价值为Vi，背包的容量为C。如何选择装入背包的物品，可以使得装入背包中物品的总价值最大？

输入

每组输入包括三行，
第一行包括物品个数n，以及背包容量C。
第二、三行包括两个一维数组，分别为每一种物品的价值和重量。

输出

输出包括两行，第一行为背包的最大总价值，第二行为所选取的物品。
例如：最大总价值=15，物品选取策略为11001。数据保证答案唯一。

样例输入

5 10
6 3 5 4 6
2 2 6 5 4

样例输出

15
11001

import java.util.Scanner;
public class Main {public static void main(String[] args) {Scanner scanner=new Scanner(System.in);int n;int c;int[] w,v;int[][] dp;while(scanner.hasNext()) {n=scanner.nextInt();c=scanner.nextInt();w=new int[n+1];v=new int[n+1];dp=new int[n+1][c+1];for(int i=1;i<=n;++i) {v[i]=scanner.nextInt();}for(int i=1;i<=n;++i) {w[i]=scanner.nextInt();}for(int j=0;j<=c;++j) {if(j>=w[n]) {dp[n][j]=v[n];}}//动态规划for(int i=n-1;i>=1;i--) {for(int j=1;j<=c;++j) {if(j<w[i]) {dp[i][j]=dp[i+1][j];}else {dp[i][j]=Math.max(dp[i+1][j], dp[i+1][j-w[i]]+v[i]);}}}int ans=dp[1][c];		System.out.println(ans);	Gouzao(n,c,w,v,dp);}}private static void Gouzao(int n, int c, int[] w, int[] v, int[][] dp) {for(int i=1;i<n;++i) {if(dp[i][c]==dp[i+1][c]) {System.out.print("0");}else {System.out.print("1");c=c-w[i];}}int last=(dp[n][c]>0?1:0);System.out.println(last);}
}

8. 扩展：空间压缩

我们注意到每次递推第i行都是用下面一行（第i+1行）的最优值，如果只用一个一维数组dp[]来存储这些值，那么

递推第i行前，dp[i]=m(i+1,j)

递推第i行后，dp[i]=m(i,j)（覆盖掉原来的值）

而在计算递推第i行时的m()数组的值，有两种选择变化：

1）不放，背包当前产生价值仍为m(i+1，j)，即dp[i]保持不变

2）放入，调整背包容量j-w_i，背包当前产生价值为m(i+1, j-w_i)+v_i，即dp[j]=dp[j-w_i]+v_i

但是求解dp[]数组时，必须保证dp[j-w_i]还是m(i,j-w_i)的值，考虑到每次递推都会覆盖掉原来dp[]数组中的值，如当j的值从小往大变化，即我们从左往右求解时dp[j-w_i]已经是m(i+1,j-w_i)的值了；（读者可自行推演，如果这样上一题的答案会是30）

因而我们得从右往左求解，即j从大往下变化

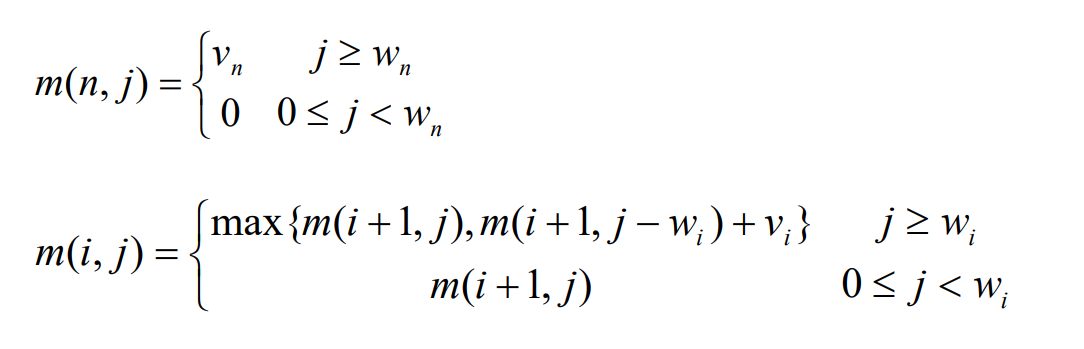
//动态规划
for(int i=n;i>=1;i--) {//j从大往下变化,保证dp[j-wi]还是m(i,j-wi)的值for(int j=c;j>=0;--j) {if(j>=w[i]) {dp[j]=Math.max(dp[j], dp[j-w[i]]+v[i]);}}
}