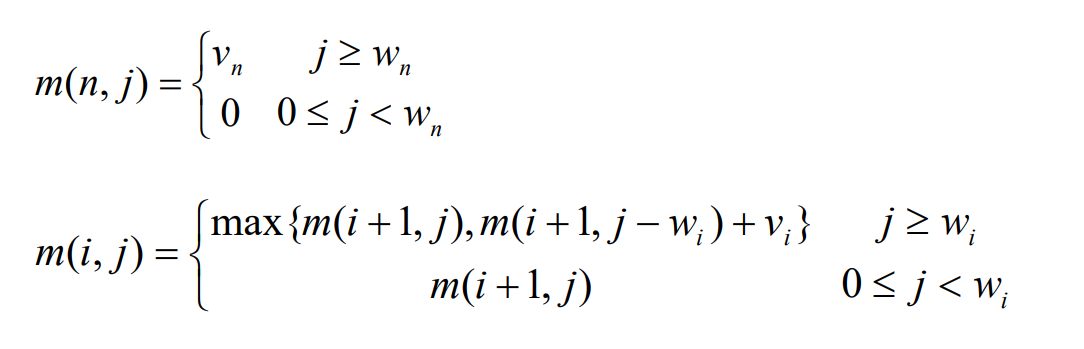视频教程讲解

【Python算法系列】动态规划2-01背包问题&完全背包问题
【Python算法实战】背包问题

题目介绍

原题链接：NC145 01背包
描述
已知一个背包最多能容纳体积之和为v的物品
现有 n 个物品，第 i 个物品的体积为 vi , 重量为 wi
求当前背包最多能装多大重量的物品？
数据范围： $\le v \le 1000 ，1 \le n \le 1000，1 \le v_i \le 1000，1 \le w_i \le 1000$
进阶： $\cdot v)$
示例1
输入：
```
10,2,[[1,3],[10,4]]
```
返回值：4
说明：第一个物品的体积为1，重量为3，第二个物品的体积为10，重量为4。只取第二个物品可以达到最优方案，取物重量为4
示例2
输入：
```
10,2,[[1,3],[9,8]]
```
返回值：11
说明：两个物品体积之和等于背包能装的体积，所以两个物品都取是最优方案

题解1：二维列表

二维列表的这种理解起来比较简单一些，如果不太熟悉，也可以参考本文开头的视频教程，另外值得注意的是，我没有使用题目中自带的类名，而还是采用的打印的方式进行，关于解包变量可以参考：Python3使用exec函数将输入进来的结果的字符串的值解包成变量的值

V, n, vw = 1, 1, []
exec('V, n, vw = ' + input())
dp = [[0 for i in range(V+1)] for j in range(n+1)]
for i in range(1, n+1):for j in range(1, V+1):if vw[i-1][0] > j:dp[i][j] = dp[i-1][j]else:dp[i][j] = max(dp[i-1][j], vw[i-1][1]+dp[i-1][j-vw[i-1][0]])
print(dp[-1][-1])

在这里插入图片描述

题解2：一维列表（滚动数组）

视频教程可以参考：听懂不翻车系列之–背包问题（01背包完全背包多重背包二维费用背包），从40分30秒开始至最后

V, n, vw = 1, 1, []
exec('V, n, vw = ' + input())
dp = [0 for j in range(V+1)]
for i in range(1, n+1):for j in range(V, 0, -1):if j >= vw[i-1][0]:dp[j] = max(dp[j], vw[i-1][1]+dp[j-vw[i-1][0]])
print(dp[-1])

在遍历时，注意是range(V, 0, -1)，也就是从后往前推进。因为如果是从前往后推进，那么dp[j-vw[i-1][0]]的值就会是本轮次的计算结果，而不是上一轮次的计算结果，我们在使用二维列表处理时会发现本次的计算结果都是基于上一轮次的结果。如果是在本轮次的上一个更小的结果之上进行推进，那么结果将会变成处理完全背包的问题（每个物品可以取任意多次，而不是最多只能取一次。）
在这里插入图片描述