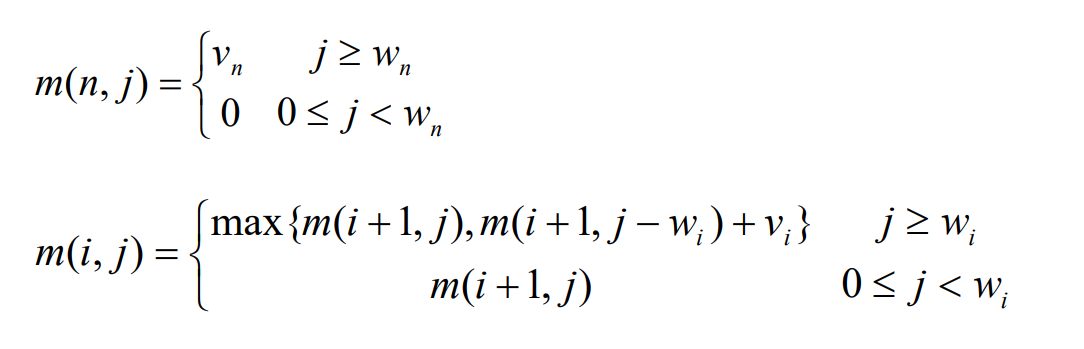参考学习网址:
https://www.bilibili.com/video/av33930433?from=search&seid=10637513335818789097
https://www.cnblogs.com/anzhengyu/p/11408466.html
问题描述:
给定 n 件物品,物品的重量为 w[i],物品的价值为 v[i]。现挑选物品放入背包中,假定背包能承受的最大重量为 c,问应该如何选择装入背包中的物品,使得装入背包中物品的总价值最大?
思路:
刚开始接触到这个题目的想法是将单位价值最大次大…的几个物品依次装入背包(对单位价值的物品进行排序,从大到小),如果这个装不下就判断下一个是否能装入,直到判断完所有的物品,从而使背包中价值最大。可是这个做法只能通过一些测试,大部分测试通过不了。其实,这是一种贪心算法的思想,这种做法并不能保证背包最终被装满,这些剩余的空间就造成了价值的降低。贪心算法是一种只考虑局部最优的方法,而不是整体最优的方法,所以这个算法思想不是对所有问题都能求得整体最优解就比如这道01背包。
所以这里使用动态规划的思想,即不做重复运算,依次取出一件物品装入容量为1到c的背包,最终得到容量为c时能装入物品价值最大为多少。
我们只用考虑两种情况,装入和不装入。

这里dp[i][j]表示只看前i个物品,背包体积为j的情况下,总价值最大是多少。
不装入:如果在背包体积为j的情况下,不装入第i个物品,那么dp[i][j]就取之前背包体积为j的情况下,装入第i-1个物品时的最大价值,即dp[i-1][j]。
状态转移公式为:dp[i][j]=dp[i-1][j]
装入:在背包体积为j的情况下,如果装入第i个物品就需要与同背包体积时装入i-1个物品的最大价值做对比取最大值填入dp[i][j]。选取第i个物品时,总价值为装入的物品i的价值+背包还剩体积的最大价值。
状态转移公式为:dp[i-1][j-v[i-1]]+w[i-1] (遍历物品次数从1开始,价值体积索引-1)
n, c = map(int, input().split())
v_w = []
for i in range(n):v_w.append(list(map(int, input().split())))dp = [[0 for i in range(c+1)] for j in range(n+1)]for i in range(1, n+1):for j in range(1, c+1):dp[i][j] = dp[i-1][j]if j >= v_w[i-1][0]:dp[i][j] = max(dp[i][j], dp[i-1][j-v_w[i-1][0]]+v_w[i-1][1])print(dp[-1][-1])
以上代码就可以得到最优的01背包最大价值解,但是我们发现dp是用二维列表来存储最大价值,但我们只要背包容量为c时所能装的物品最大价值,这样就会造成很大的内存资源消耗。所以我们能不能将二维列表改为一维列表来存储最大价值呢?
通过上面的二维代码,可以发现dp[i]只与dp[i-1]有关。所以我们只需要让dp来存储上一次(选取物品i-1时)的最大价值。
由于在能装入的情况下,背包有剩余空间 (i-1),我们需要i-1体积时的最大价值,所以不能正向改变dp中的最大价值,这时候就需要倒着改变dp中的最大价值。

dp[i]表示背包容量为i时,选取多少物品得到的总价值最大是多少。
不装入:dp[i]=dp[i],在代码中可以省略
装入:和之前二维类似,dp[j-v[i-1]]+w[i-1]
n, c = map(int, input().split())
v_w = []
for i in range(n):v_w.append(list(map(int, input().split())))dp = [0 for i in range(c+1)]for i in range(n):for j in range(c, -1, -1):if j >= v_w[i][0]:dp[j] = max(dp[j], dp[j - v_w[i][0]] + v_w[i][1])print(dp[-1])
运行结果:
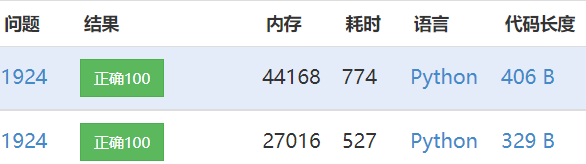
上面为二维运行结果,下面为一维运行结果。可以看出运行内存和时间均得到了优化。
运行测试网址:https://www.dotcpp.com/oj/problem1924.html
欢迎大家采纳和指正!!!
如果大家有更优的解法,欢迎在评论区留言。