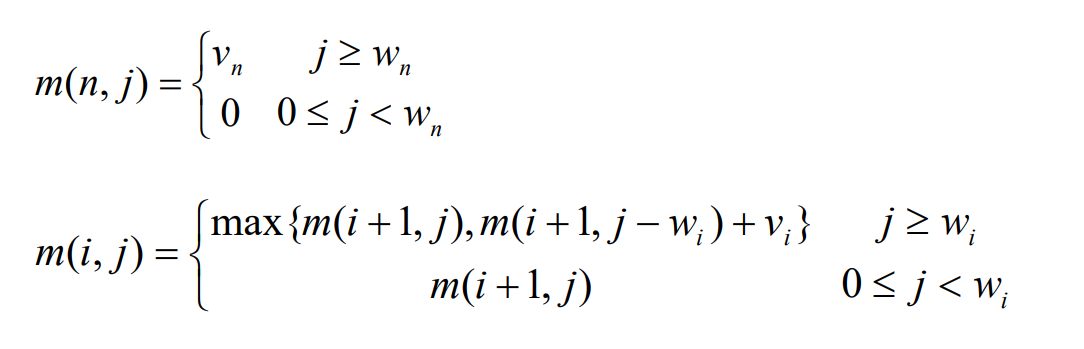动态规划 - 01背包问题
1.使用递归遍历(穷举)求解:
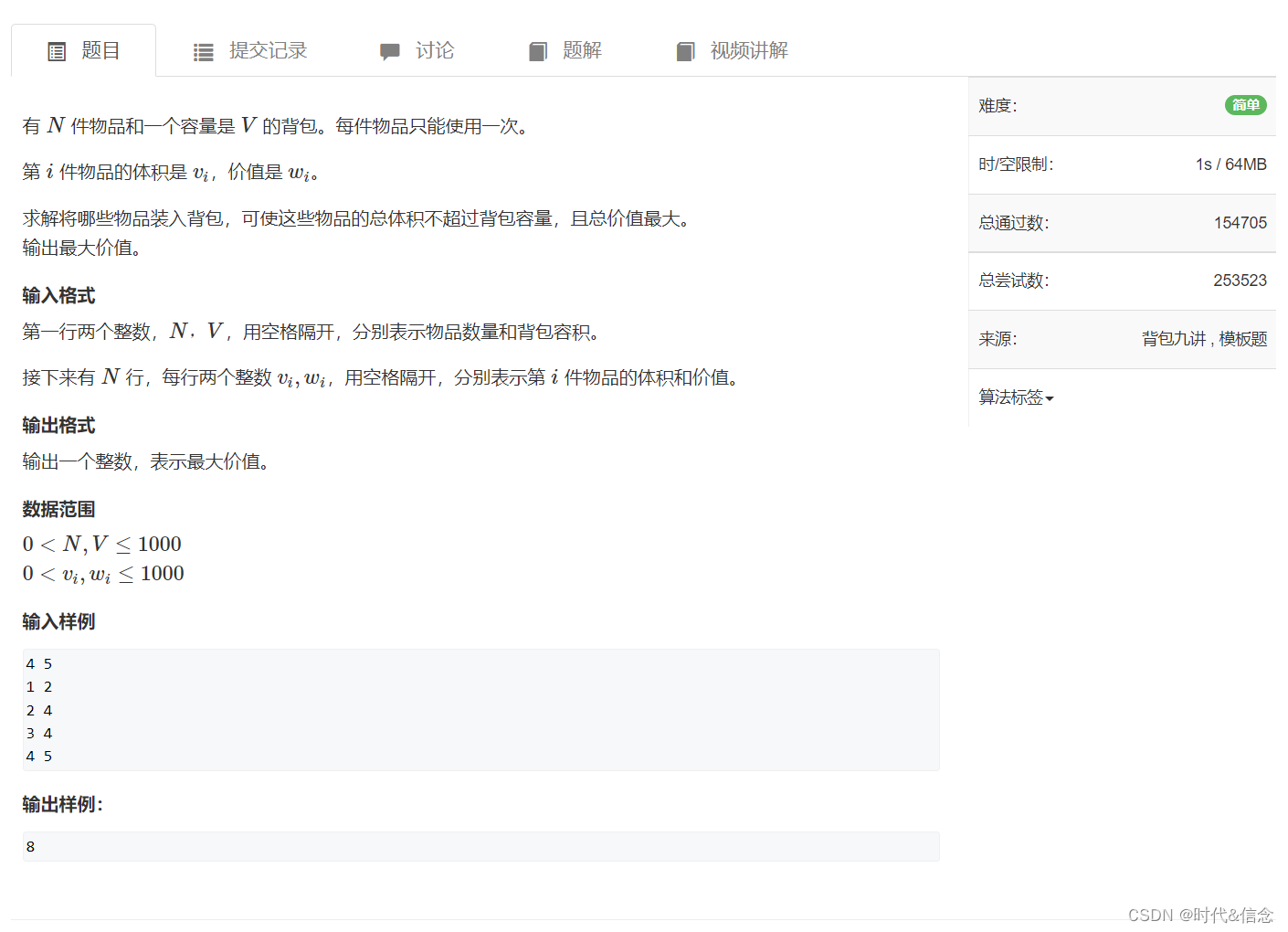
01背包问题:给定 n 种物品和一个重量(容量)(限定条件)为 w 的背包,物品 i 的重量是 wi,其价值为 vi。(每种物品只有一个)问:如何选择装入背包的物品,使得装入背包中的物品的价值最大。
//VC6.0--------------------------
#include"stdafx.h"
#include <cmath>
#include <iostream>
using namespace std;//----------全局变量------------
#define n 4 //number //物品数量
#define max_w 9 //weight //可承受重量(最大重量)
int value[n]={2,3,4,5}; //物品价值
int weight[n]={3,4,5,6}; //物品重量
//最大价值 以及解向量
int max_v=0; int x[n]={0};
int nx[n]={0}; //当前解的情况
//-----------------------递归-----------------------
void beibao01(int i,int v,int w) //第i个物品 总价值 总重量
{//物品已遍历完毕if(i>n-1) return; //将第i个物品放入 改变解向量 if((w+weight[i]) <= max_w){nx[i]=1;//如果大于之前的解的最大价值 则更新最大价值以及解向量if((v+value[i]) > max_v){max_v = v+value[i];for(int k=0;k<n;k++) x[k]=nx[k];}beibao01(i+1,v+value[i],w+weight[i]);}//不放第i个物品 刷新解向量 for(int k=i;k<n;k++) nx[k]=0;beibao01(i+1,v,w);
}//------------------------------------------------------
void main()
{beibao01(0,0,0);//输出答案cout<<max_v<<endl;for(int k=0;k<n;k++) cout<<x[k]<<" ";
}max_w=8: 
2. 动态规划算法求解
//VC6.0--------------------------
#include "stdafx.h"
#include <cmath>
#include <iostream>
using namespace std;int max(int a,int b){if(a>b) return a;else return b;
}
void solution(int i,int j);//----------全局变量------------
#define n 4 //number //物品数量
#define max_w 9 //weight //可承受重量(最大重量)
int value[n]={2,3,4,5}; //物品价值
int weight[n]={3,4,5,6}; //物品重量int max_v=0; int x[n]={0}; //最大价值 以及解向量
int real_w=0; //包含最大价值背包的实际重量
//动态规划表 dynamic programming table
int dpt[n][max_w+1]={0}; // dpt[i][j]=k 表示前i个物品装在承重为j的背包中的最大价值为k//-----------------------状态转移方程-----------------------
//不考虑单个物品重量超过max_w 不考虑单个物品价值为0 等特殊情况
void beibao01() //解出动态规划表以及 最大价值 背包实际重量 解向量
{int i,j;//先填写第一行表for (j = 0; j <= max_w; j++)if(j >= weight[0])dpt[0][j] = value[0];elsecontinue;//由递推式 填完表for (i = 1; i < n; i++) {for (j = 1; j <= max_w; j++) {//容量为j的背包装不下 第i个物品if (j < weight[i])dpt[i][j] = dpt[i-1][j];//能装下 装完第i个物品之后背包重量为j 则其价值为 dpt[i-1][现在重量-第i物品重量] + 第i物品价值else{//取其最大值 即为最优子策略dpt[i][j] = max(dpt[i-1][j], dpt[i-1][j-weight[i]] + value[i]);if(dpt[i][j] > max_v){max_v = dpt[i][j];real_w = j;}}}}//求一个最优解solution(n-1,real_w);
}
//----------求解向量-------------
void solution(int i,int j)
{//第一个物品是否放入背包?if(i == 0){//没有放入if(j == 0) x[i] = 0;else x[i] = 1;}else{//第i个物品没有放入包内 寻找上一个最优子策略if(dpt[i][j] == dpt[i-1][j]){x[i] = 0;solution(i-1,j);}//第i个物品放入了包内 寻找上一个最优子策略else{x[i] = 1;solution(i-1,j-weight[i]);}}
}
//------------------------------------------------------
void main()
{int i,j;beibao01();//输出答案cout<<"物品价值:"<<endl;for (i = 0; i < n; i++) cout<<value[i]<<" ";cout<<endl;cout<<"物品重量:"<<endl;for (i = 0; i < n; i++) cout<<weight[i]<<" ";cout<<endl;cout<<"动态规划表:"<<endl;for (i = 0; i < n; i++) {for (j = 0; j <= max_w; j++) {cout << dpt[i][j] << ' ';}cout << endl;}cout<<"实际重量:"<<real_w<<endl;cout<<"最大价值:"<<max_v<<endl;cout<<"解向量:";for(int k=0;k<n;k++) cout<<x[k]<<" ";cout<<endl;
}max_w=8: 
max_w=9: 
3.对2进行简化
//VC6.0--------------------------
#include "stdafx.h"
#include <cmath>
#include <iostream>
using namespace std;
//----------全局变量(输入信息)------------
#define n 4 //数量
#define max_w 8 //最大重量
int value[n]={2,3,4,5}; //价值
int weight[n]={3,4,5,6}; //重量//----------最大值函数--------
int max(int a,int b){if(a>b) return a;else return b;
}
//-----------------------填写动态规划表-----------------------
int beibao01(int *x)
{int i,j;int dpt[n][max_w+1]={0}; //动态规划表int max_v; //最大价值int real_w; //实际重量//--------------第一行------------for (j = 0; j <= max_w; j++)if(j >= weight[0])dpt[0][j] = value[0];//--------------其余行------------for (i = 1; i < n; i++) {for (j = 1; j <= max_w; j++){if (j < weight[i])dpt[i][j] = dpt[i-1][j];else{dpt[i][j] = max(dpt[i-1][j], dpt[i-1][j-weight[i]] + value[i]);}}}//求最大价值 以及实际重量for (j = 1; j <= max_w; j++){if(dpt[n-1][j] > max_v){max_v = dpt[n-1][j];real_w = j;}}//求一个最优解for (i = n-1; i > 0; i--) {if(dpt[i][real_w ] != dpt[i-1][real_w ]){x[i] = 1;real_w = real_w-weight[i];}}if(real_w != 0) x[0] = 1;//返回最大值return max_v;
}//------------------------------------------------------
void main()
{//解向量int x[n]={0};//输出答案cout<<"最大价值:"<<beibao01(x)<<endl;cout<<"解向量:";for(int k=0;k<n;k++) cout<<x[k]<<" ";cout<<endl;
}max_w=8: