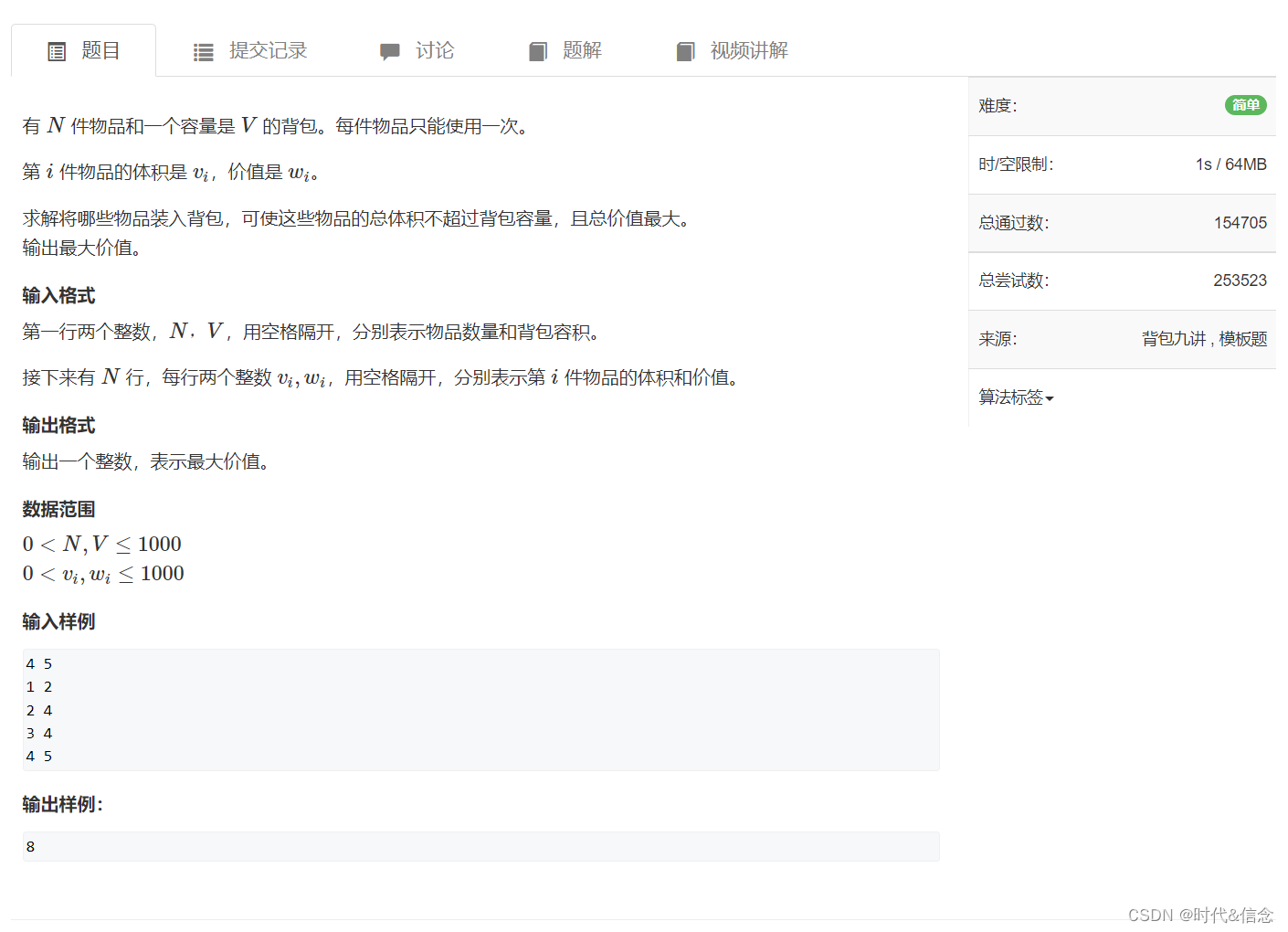
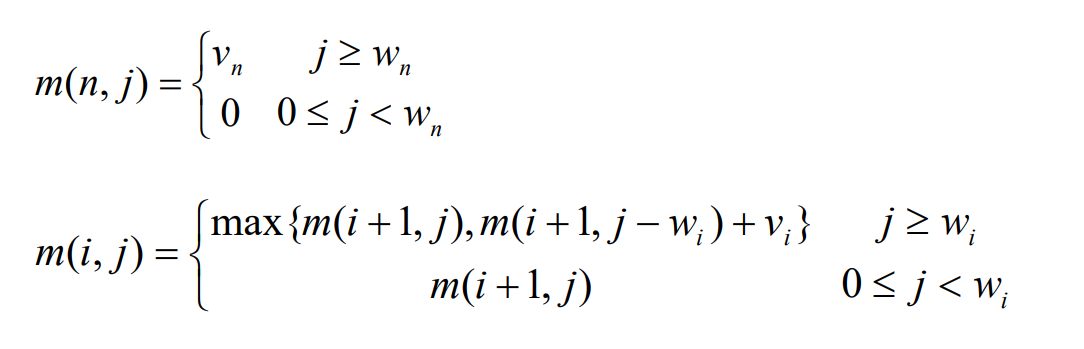题目描述:
解题思路:
整体思路:
利用动态规划,其目的就是将原问题分解成几个子问题,通过求解简单的子问题,把原问题给解决,就比如斐波那契数列方程:
f[i]=f[i-1]+f[i-2];
动态规划的核心就是找到原问题与子问题的关系,并列出动态转移方程。
实现方法:
这里我们可以定义一个二维数组,dp[i][j]表示对于背包容量为j的背包,前i个物品的最优解,即最大价值。
对于一个物品,可以分两种情况:
不选:对于dp[i][j],不选第i个物品时,dp[i][j]的最优解就是dp[i-1][j]的最优解
选:如果选择,我们就让背包容量减去第i件的物品体积,让dp加上物品价值,即dp[i][j]=dp[i-1][j-v[i]]+w[i];
这样我们就得到了状态转移方程,如果要计算对于前N个物品背包容量为V的背包的最优解,只需要一层一层往前推,通过前面的子问题,求得最终答案。
状态转移方程:
dp[i][j]=max(dp[i-1][j],dp[i-1][j-v[i]]+w[i]);
代码和注释:
#include <iostream>
using namespace std;
int dp[1010][1010];
int v[1010],w[1010];//体积和价值
int main(){int N,V;int i,j;//输入数据cin>>N>>V;//商品个数和背包容量for(i=1;i<=N;i++){cin>>v[i]>>w[i];//体积和价值}for(i=1;i<=N;i++)//依次遍历从第1个物品到第N个物品{for(j=1;j<=V;j++)//依次遍历从0~背包容量V{if(j<v[i])//如果背包容量小于物品体积{dp[i][j]=dp[i-1][j];//最优解就是上一个物品时的最优解}else//否则就是背包容量大于等于物品体积{dp[i][j]=max(dp[i-1][j],dp[i-1][j-v[i]]+w[i]);//拿或者不拿,选最优}}}cout<<dp[N][V]<<endl;//输出前N个商品,背包容量为V的最优解return 0;
}参考自:https://blog.csdn.net/q1411687596/article/details/104827473