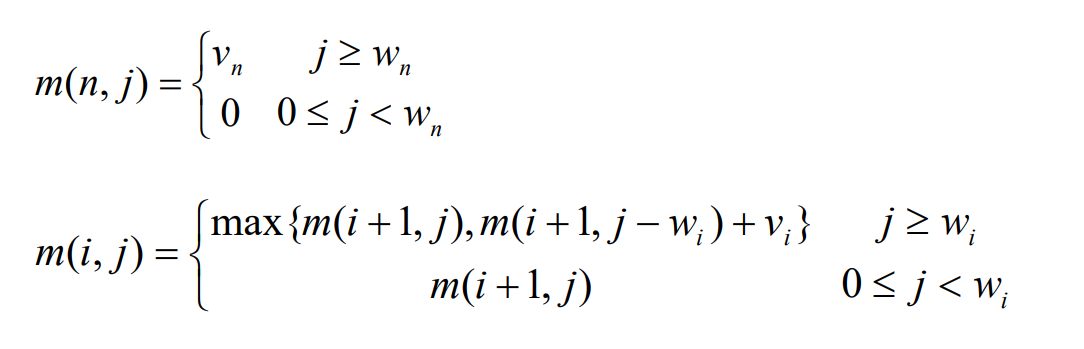动态规划——背包问题（01背包问题）

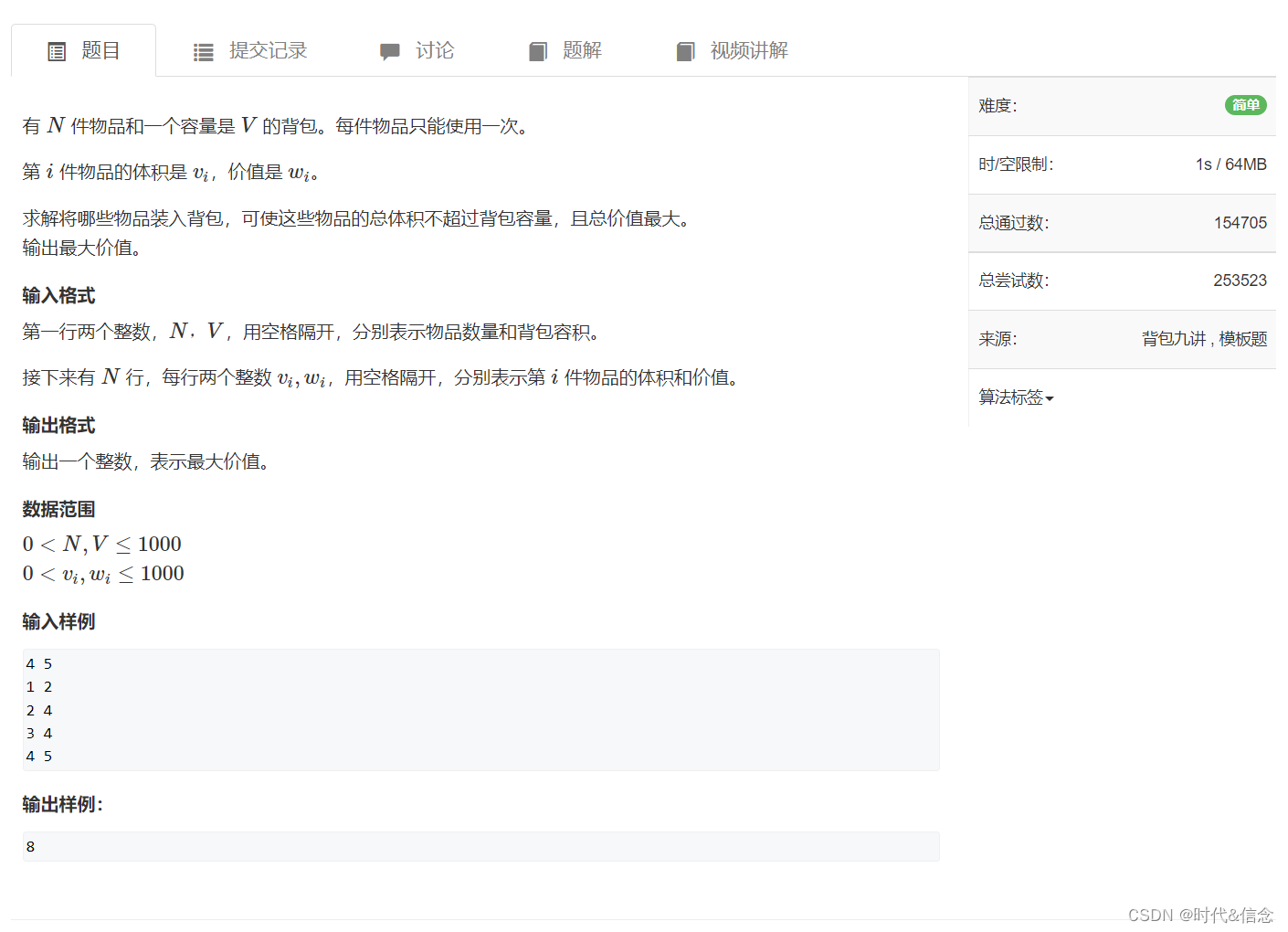
01背包问题(求最大价值)：

有N件物品和一个最多能背重量为W的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每个物品只有一样（只能用一次），求解哪些物品放入背包能使价值总和最大？
背包问题可以用二维的动态规划去求解。

• 对于dp数组的含义理解：dp[i][j]表示从编号0~i的物品中选取物品，装入容量为j的背包中所能得到的最大价值为dp[i][j]。
• 接下来来考虑dp[i][j]的递推式：dp[i][j]可以由两个方向推出：
  1、本轮不放物品，则本轮价值与从编号0~i - 1的物品中选取物品，装入容量为j的背包中所能得到的最大价值相同，即dp[i][j] = dp[i - 1][j]。
  2、本轮放物品，物品从0~i的物品中挑选，记物品为j（0≤j≤i）,则本轮价值为从编号0到i - 1的物品中选取物品装入容量为j - weight[i]的背包价值再加上选取的这个物品的价值（value[i]）。
  dp[i][j]应该从两个中取最大的，即dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i])。
  考虑初始化：
  由递推式可以看出后面的状态依赖于前面的状态，所以要初始化第一行以及第一列.。即dp[i][0] = 0，
  dp[0][j] 为只有第一个物品放入背包的价值(如果背包能放下第一个物品的话)。
• 考虑遍历顺序：
  由递推式可以看出遍历顺序从上到下，从左到右。那么就需要两个for循环。那么就有两个遍历顺序
  1、先遍历背包容量，在遍历物品(即先行后列)。表示将物品依次分别放入背包容量是0至W的背包中，得到最大价值。
  2、先遍历物品，在遍历背包容量（即先列后行）。这表示先固定下来一个容量为j的背包，将所有物品尝试放入，得到最大价值。
  从递推式可以看出dp[i][j]至于左上部分有关，这两种遍历顺序都能保证在dp[i][j]时左上部分已经构建完毕，所以这两种遍历顺序都可以
  

//dp数组初始化
vector<vector<int>> dp(N, vector<int>(W + 1, 0));
for (int j = 0; j <= W + 1; ++j) {if (weight[i] <= W) {dp[0][j] = value[0];}
}//遍历
for (int i = 1; i < N; ++i) {for (int j = 0; j <= W; ++j) {if (j < weight[i]) dp[i][j] = dp[i - 1][j];else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);}
}return dp[N - 1][W];

问题优化

二维的递推式为dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]),我们可以看到，下一层的数据是依赖上一层的数据推出的（即dp[i] 可以先把上一层的数据复制下来，再在此基础上进行操作）。由于每一层的数据仅和与自己相邻的上一层的数据相关，我们可以将二维数组压缩成一维数组。
即将 dp[i][j]变成dp[j]。

• dp[j]的含义：背包容量为j的背包可以容纳的物品的最大价值总和为dp[j];
• 递推关系：
  dp[j]可以由两个方向得出，设本次放的物品为i：
  1、本次不放物品：则dp[j] = dp[j]，即背包价值总和不变
  2、本次放物品： 则dp[j] = dp[j - weight[i]] + value[i]，即背包容量为j - weight[i]的背包的最大价值总和加上本次放的物品的价值。
  两者取最大，即dp[j] = max(dp[j], dp[j - weight[i]] + value[i])。
• 遍历顺序：
  一维数组要么从前往后遍历，要么从后往前遍历。如果从前往后遍历，那么后面的必定会用到前面的数据，就会发生重复放置的问题。
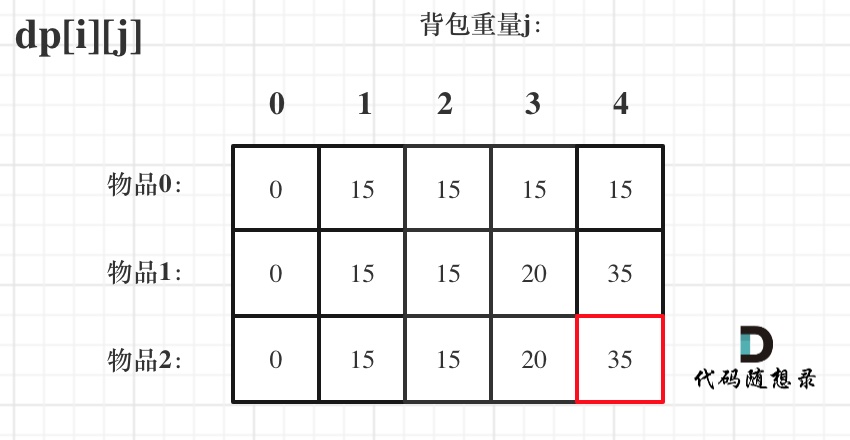
  举个例子
  
  dp数组如上，可以看到背包容量为2的背包计算了两次物品1。这是由于计算dp[2]的时候使用了dp[1]，而此时dp[1]已经放置了物品1，当dp[2]再次利用物品1计算时就会出现重复。因此遍历顺序必须由后向前，才能保证每个物品只使用一次。也是因此，只能先遍历物品在遍历背包
  初始化
  各个背包一开始没有物品，都为0。

vector<int> dp(W + 1);
for(int i = 0; i < N; ++i){for(int j = W; j >= weight[i]; --j){dp[j] = max(dp[j], dp[j - weight[i]] + value[i])}
}
return dp[W];

01背包问题(求方案数)：

有N件物品和一个最多能背重量为W的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每个物品只有一样（只能用一次），求解使背包价值最大的物品组合共有几种？
这个与上面的问题主要有如下不同：

• dp[j]含义：装满背包容量为j的最大价值的物品组合数共dp[j]种。
• 递推式：
  得到dp[j]的方向：假设本次拿到的物品为i 那么dp[j]就是自己原本的方案数再加上 dp[j - weight[i]]的方案数，即 dp[j] += dp[j - weight[i]]
• 初始化：
  dp[j]是由前向后推出的，因此要初始化的是dp[0] = 1 ：装满容量为0的背包的最大价值的物品组合有一种，就是什么也不装。

vector<int> dp(W + 1);
dp[0] = 1;
for(int i = 0; i < N; ++i){for(int j = W; j >= weight[i]; --j){dp[j] += dp[j - weight[i]];}
}
return dp[W];