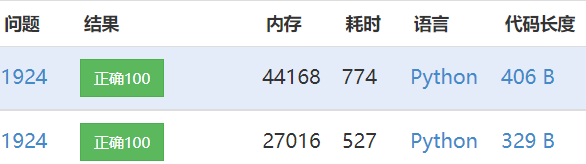
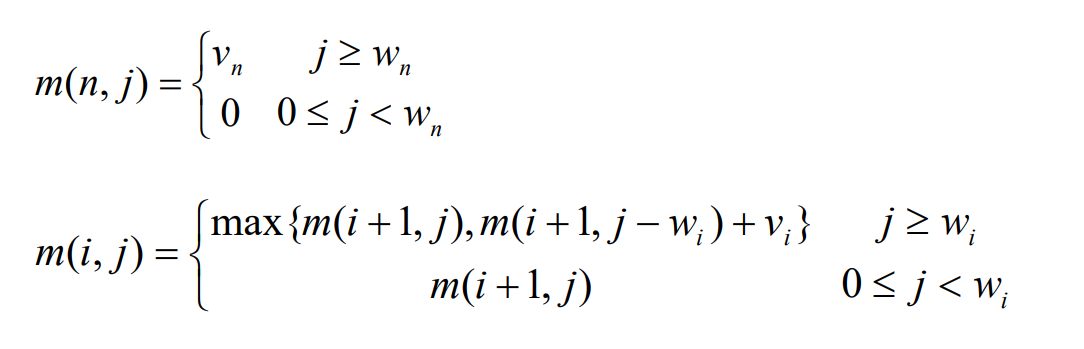01背包问题一般是利用动态规划进行解题的,这里通过leetcode1049来讲解01背包的解题思路以及如何对01背包应用题目转换和理清思路
01背包问题:
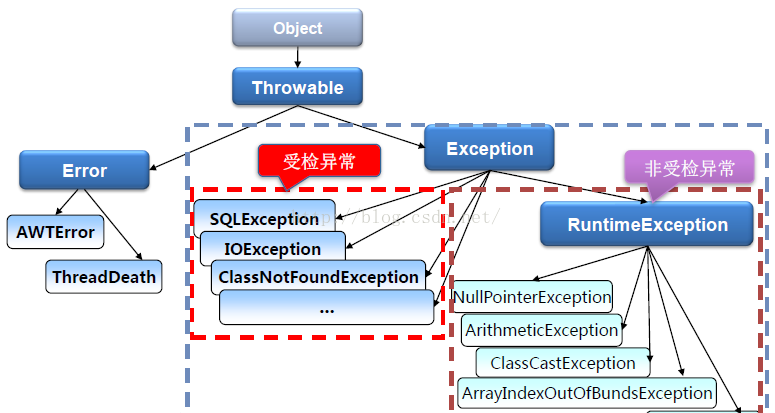
这里借用学习公众号代码随想录的一张图来说明背包问题的种类

对于面试的话,其实掌握01背包,和完全背包,就够用了,最多可以再来一个多重背包。
首先来看01背包问题的描述
有N件物品和一个最多能被重量为W 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。
对于这种问题第一印象就是将所有可能的组合遍历出来,每一件物品都有取与不取两种状态,但是这种暴力解法的时间复杂度是O(2^N),对一半题目来说太高了,需要动态规划来降低复杂度。
解题思路:
1.还是从五步骤开始,先是定义数组,确定数组下标含义,在01背包问题中需要迭代更新的有两个变量是物品和重量,我们可以理解为在i个物品j重量的前提下,算出i+1个物品j重量的组合或者i个物品j+1重量的组合,所以数组的定义是dp[i][j]

2.那么可以有两个方向推出来dp[i][j],
由dp[i - 1][j]推出,即背包容量为j,里面不放物品i的最大价值,此时dp[i][j]就是dp[i - 1][j]
由dp[i - 1][j - weight[i]]推出,dp[i - 1][j - weight[i]] 为背包容量为j - weight[i]的时候不放物品i的最大价值,那么dp[i - 1][j - weight[i]] + value[i] (物品i的价值),就是背包放物品i得到的最大价值
所以递归公式:dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
同时我们可以从递推公式中看到dp[i]的变化跟dp[i-1]行的变化有关,这种只跟前面一行状态以及当前行已经更新过的状态有关的情况下,可以将数组进行压缩变成一维数组即dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);对于已经被覆盖的数组,递推公式中是完全用不上的。后面为了方便讲解还是继续使用二维数组。
3.数组初始化
关于初始化,一定要和dp数组的定义吻合,否则到递推公式的时候就会越来越乱。
我们看递推公式中dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i])可以看出有两个要初始化的地方dp[i]的状态跟dp[i-1]有关,所有要初始化第0行即物品0号放入各种容量背包中重量大小,但是这里会在遍历中进行更新;还和j - weight[i]有j==weight[i]的情况,所以还要初始化dp[i][0]第0列,当容量为0时候,重量最大上限也是0,所以不用更改。综上所述,需要初始化的地方就是第0行。
首先我们要考虑01背包的条件,每个物品只有一件,不能重复放入,所以必须要从右往左进行倒序遍历,从左往右正序遍历会导致物品放入多次。
初始化递推dp[0][j] = dp[0][j - weight[0]] + value[0];举个反例:0号物品重量为1,如果是正序遍历的话,dp[0][0] = 0,dp[0][1] = 1,那么dp[0][2]=2,就相当于放入两次了。
4.遍历顺序
动态规划是比较看重遍历顺序的,遍历顺序不一样,可能得到的结果会完全不一样。但是在这里哪种遍历顺序都可以,先物品再容量和先容量再物品都可以。
leetcode:1049
有一堆石头,每块石头的重量都是正整数。
每一回合,从中选出任意两块石头,然后将它们一起粉碎。假设石头的重量分别为 x 和 y,且 x <= y。那么粉碎的可能结果如下:
如果 x == y,那么两块石头都会被完全粉碎;
如果 x != y,那么重量为 x 的石头将会完全粉碎,而重量为 y 的石头新重量为 y-x。
最后,最多只会剩下一块石头。返回此石头最小的可能重量。如果没有石头剩下,就返回 0。
官方例子:
输入:[2,7,4,1,8,1]
输出:1
解释:
组合 2 和 4,得到 2,所以数组转化为 [2,7,1,8,1],
组合 7 和 8,得到 1,所以数组转化为 [2,1,1,1],
组合 2 和 1,得到 1,所以数组转化为 [1,1,1],
组合 1 和 1,得到 0,所以数组转化为 [1],这就是最优值。
解析
咋一看,这题目跟01背包毫无关系,实际上需要转化思维方式,这是一道01背包的应用题。
首先两两石头进行粉碎,什么情况下能让剩下重量最小就是两块石头重量很接近的时候。那么这道题的解题思路就是将石头分成两堆,让他们重量相近,实际上就是重量少的那堆的重量总和尽量接近于原石头堆stones一半的重量。这就好办了,题目已经转化为背包所容纳的重量为stones/2,物品为石头数组的01背包问题。就可以利用上面01背包的解题思路进行解题了。
代码:
public int lastStoneWeightII(int[] stones) {int sums = 0;for(int i=0;i<stones.length;i++){sums += stones[i];}int sum = sums/2;int[] dp = new int[sum+1];for(int i=0;i<stones.length;i++){for(int j = sum;j>=stones[i];j--){dp[j] = Math.max(dp[j],dp[j-stones[i]]+stones[i]);}}return (sums-dp[sum])-dp[sum];}