目录
前言
1.构造函数和原型
1.1使用prototype解决内存浪费的问题
1.2constructor构造函数构造器构造函数
2.原型链
2.1js中成员查找规则
2.2原型对象this指向
2.3扩展内置对象
3.call作用
4.继承
4.1利用原型对象继承
写在最后
前言
哈喽哈喽大家好,因为最近的事情多一点,所以停更了几天,时隔半个月,我山鱼又回来了,以后会持续更新的烟花🎉🎉🎉【本篇主要更新了es5的对象原型prototype和call的使用,以及原型对象内部的方法继承和指向回】
1.构造函数和原型
1.1使用prototype解决内存浪费的问题
缺点:存在内存浪费的问题,

如果有俩对象或者更多就会对一个复杂数据类型进行空间的多次开辟

构造函数原型prototype原型对象主要解决了内存浪费的问题构造函数通过原型分配的函数是所有对象所共享的。在JavaScript里每一个构造函数都有一个 prototype属性,指向另一个对象。这个prototype就是一个对象,prototype这个对象的所有属性和方法,都会被构造函数所拥有。这时候就可以使用prototype把方法放到里面供该对象所有的实例对象使用。


对象原型_ proto_ 对象
对象都会有一个属性_ proto_ 指向构造函数的 prototype原型对象,之所以我们对象可以使用构造函数prototype原型对象的属性和方法,就是因为对象有_ proto_ 原型的存在。

sy的 _ proto_ 和sym的 _ proto_ 是一样的方法的查找规则:首先先看sy,sym对象身上是否有sing 方法,如果有就执行这个对象上的sing ,因为存在_ _ proto _ _,就去构造函数原型对象Prototype的存在,就去构造函数原型对象Prototype身上去查找sing这个方法(简单来说就是,我自己有就使用,没有就去原型对象里找)函数 和 对象创建时 会自动创建一个属性 他两指向同一个空对象

1.2constructor构造函数构造器构造函数
对象原型(_ proto _) 和构造函数( prototype )原型对象里面都有一个属性constructor属性, constructor我们称为构造函数,因为它指回构造函数本身。


他们俩里面都有constructor如果prototype里面以对象的形式添加,那么就是prototype指向变了,指向了一个新的原型对象,这个新对象里没有指向construor,需要自己手动指向一下

2.原型链
2.1js中成员查找规则
当访问一个对象的属性(包括方法)时,首先查找这个对象自身有没有该属性。 如果没有就查找它的原型(也就是._ proto _指向的prototype原型对象)。 如果还没有就查找原型对象的原型( Object的原型对象)。 依此类推一直找到Object为止( null )。


2.2原型对象this指向
1.在构造函数中,里面this指向的是对象实例shanyu
<script>function Person(uname, uage) {this.uname = uname;this.uage = uage;}// 声明一个变量然后验证this指向是不是和实例化对象相同var that;Person.prototype.skill = function () {console.log('我会吃饭');that = this;}var shanyu = new Person('山鱼', 30);shanyu.skill();console.log(that === shanyu);</script>2.3扩展内置对象
可以通过原型对象,对原来的内置对象进行扩展自定义的方法.
<script>// 自定义对象应用,给Array添加一个自定义方法Array.prototype.sum = function () {var sum = 0;for (var i = 0; i < this.length; i++) {sum += this[i];}return sum;}var arr = [1, 2, 3, 4];console.log(arr.sum());</script>数组和字符串内置对象不能给原型对象覆盖操作Array.prototype = {} 如果进行该操作就会使本来有的方法被覆盖掉,只能是Array.prototype.方法名= function(){} 的方式。

3.call作用
调用这个函数,并且修改函数运行时的this指向,有三个参数分别是thisArg 当前调用函数this的指向对象arg1 , arg2 传递的其他参数
<script>function sing(x,y) {console.log("a~a~给我已被忘情水");console.log(this);console.log(x+y);}var fn = {name: '山鱼'}// call()可以改变这个函数的this指向此时这个函数的this就指向了o这个对象sing.call(fn,1,2)</script>4.继承
通过我们打的可以看到this的指向为Son,也就是Son使用了父构造函数里面的,uname,uage


4.1利用原型对象继承
es6之前并没有extends所以可以使用构造函数和模型对象结合的方式来进行继承操作
<script>function Father(uname, uage) {this.uname = uname;this.uage = uage;}Father.prototype.eat = function () {console.log("我爱吃鸡腿");}// 子构造函数Son.prototype = new Father();Son.prototype.constructor = Son;function Son(uname, uage, swing) {Father.call(this, uname, uage);this.swing = swing;}Son.prototype.student = function () {console.log('我爱学习!!');}// 要向使用父亲原型对象里面的方法,可以实例化一下Father,然后// 这时候Son的this指向到了Father,所以我们要用constructor将this指回到Sonvar son = new Son('山鱼妹', 18, "游泳冠军!!!");// console.log(son.eat());console.log(son);console.log(Father.prototype);</script>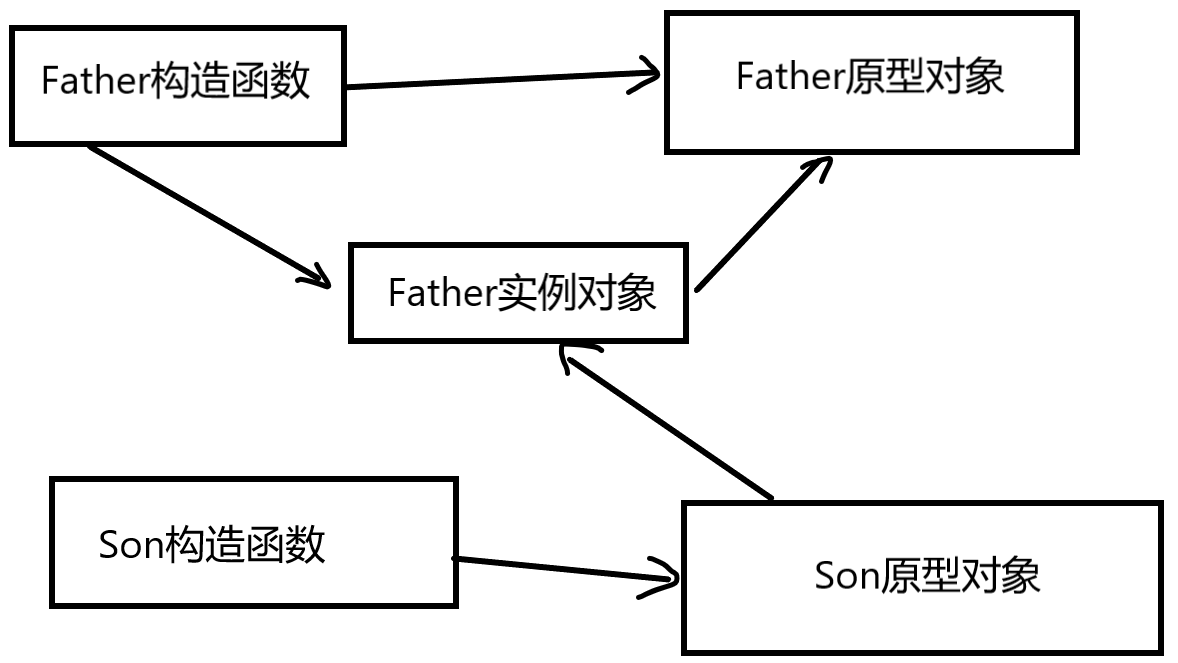
写在最后
一只蛋,如果从外面被敲开,注定只能被吃掉。如果从里面啄开,说不定是只鹰!🦅
点赞👍:您的赞赏是我前进的动力!
收藏⭐:您的支持我是创作的源泉!
评论✍:您的建议是我改进的良药!
山鱼🦈的个人社区:欢迎大家加—— 山鱼社区