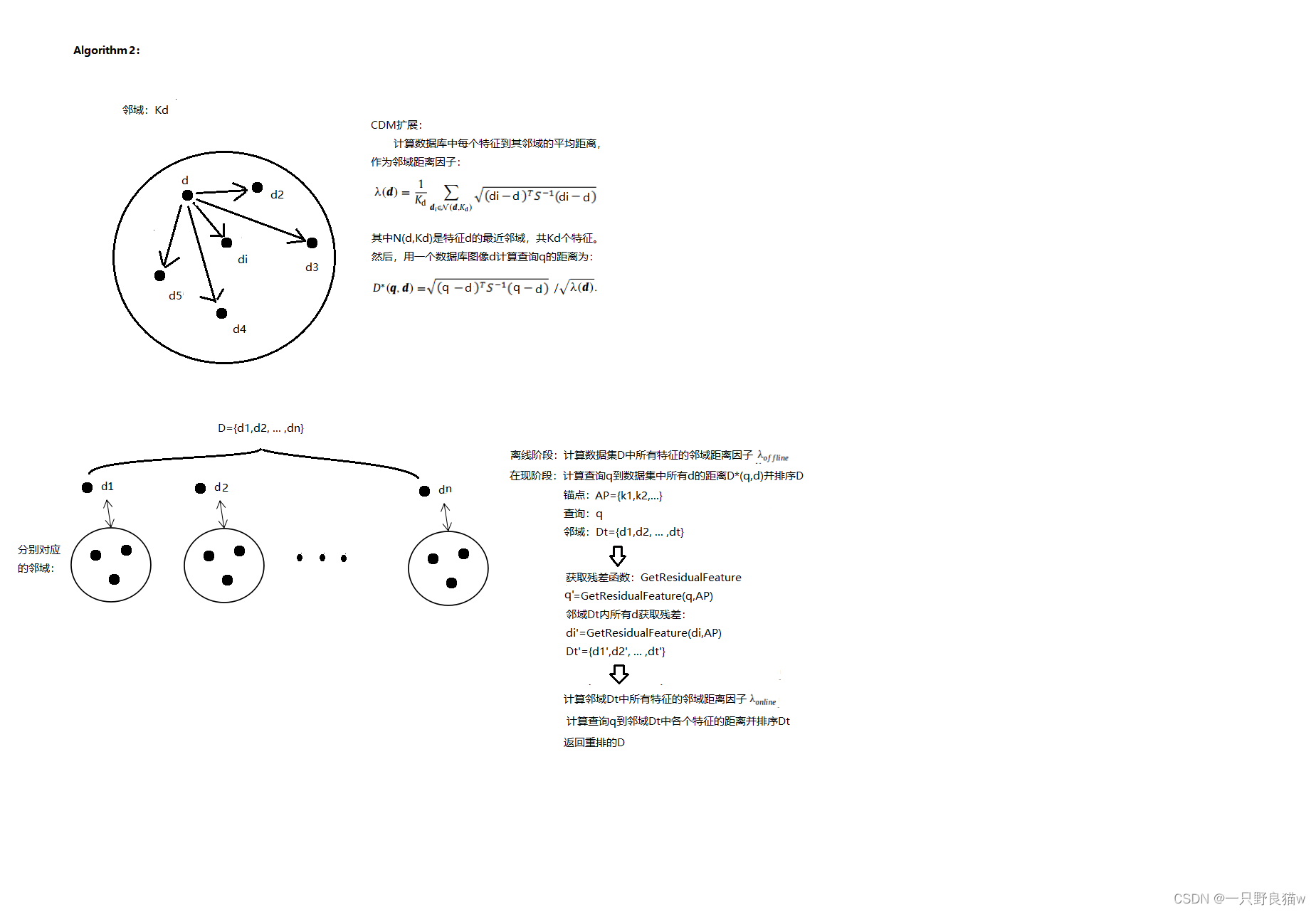
马氏距离 Mahalanobis Distance
- 1. 马氏距离定义
- 2. 马氏距离实际意义
- 2.1 欧氏距离近就一定相似?
- 2.2 归一化后欧氏距离就一定相似?
- 2.3 算上维度的方差就够了?
- 3. 马氏距离的几何意义
- 4. 马氏距离的推导
- 5. 马氏距离限制
Reference:
- 马氏距离(Mahalanobis Distance)
马氏距离(Mahalanobis Distance)是度量学习中一种常用的距离指标,同欧氏距离、曼哈顿距离、汉明距离等一样被用作评定数据之间相似度的指标。可以应对高维度线性分布的数据中各维度间非独立同分布的问题。
1. 马氏距离定义
马氏距离是一种距离的度量,可以看作是欧氏距离的一种修正,修正了欧氏距离中各维度尺度不一致且相关的问题。
单个数据点的马氏距离:
D M ( x ) = ( x − μ ) T Σ − 1 ( x − μ ) D_M(x)=\sqrt{(x-\mu)^T\Sigma^{-1}(x-\mu)} DM(x)=(x−μ)TΣ−1(x−μ)
数据点 x x x, y y y 之间的马氏距离:
D M ( x ) = ( x − y ) T Σ − 1 ( x − y ) D_M(x)=\sqrt{(x-y)^T\Sigma^{-1}(x-y)} DM(x)=(x−y)TΣ−1(x−y)
其中 Σ \Sigma Σ 为多维随机变量的协方差矩阵, μ \mu μ 为样本均值,如果协方差矩阵是单位矩阵,也就是各维度独立同分布,马氏距离就变成了欧氏距离。
2. 马氏距离实际意义
马氏距离相比欧氏距离好在哪里?举个例子:
2.1 欧氏距离近就一定相似?
举个比较常用的例子:身高和体重,这两个变量拥有不同的 unit,也就是有不同的 scale。比如身高用毫米计算,而体重用千克计算,显然差 10mm 的身高和差 10kg 的体重是完全不同的。但在欧式距离中,这将会被看做相同的差距。
2.2 归一化后欧氏距离就一定相似?
当然我们可以先做归一化来消除维度间 scale 不同的问题,但是样本分布也会影响分类。
举个一维的例子:
现在有两个类别,unit 统一,第一个类别均值为0,方差为0.1;第二个类别均值为5,方差为5。那么一个值为2的点属于第一类的概率大还是第二类的概率大?
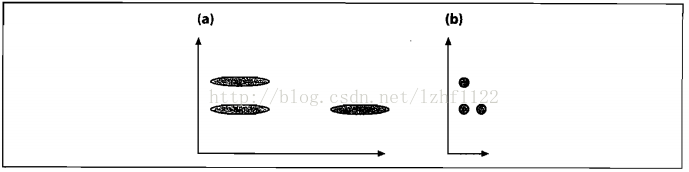
- 从距离看,应该是第一类,但直觉上显然是第二类,因为第一类不太可能达到2这个位置。
所以,在一个方差较小的维度下很小的差别就有可能成为离群点。如下图, A A A 与 B B B 相对于原点的距离是相同的。但是由于样本总体沿着横轴分布,所以B点更有可能是这个样本中的点,而A则更有可能是离群点:

2.3 算上维度的方差就够了?
还有一个问题-----如果维度间不独立同分布,样本点一定与欧氏距离近的样本点同类的概率更大吗?

可以看到样本服从 f ( x ) = x f(x)=x f(x)=x 的线性分布, A A A 与 B B B 相对于原点的距离依旧相等,显然 A A A 更像是一个离群点。
即使数据已经经过了标准化,也不会改变 A B AB AB 与原点间距离大小的相互关系。所以要本质上解决这个问题,主要针对主成分分析中的主成分来进行标准化。
3. 马氏距离的几何意义
上面搞懂了后,马氏距离就好理解了,只需要将变量按照主成分进行旋转,让维度之间相互独立,然后进行标准化,让维度同分布就好了。
由主成分分析可知,由于主成分就是特征向量方向,每个方向的方差就是对应的特征值,所以只需要按照特征向量的方向旋转,然后缩放特征值倍就可以了,得到以下结果:
 这时候的欧氏距离就是马氏距离。
这时候的欧氏距离就是马氏距离。
4. 马氏距离的推导
首先要对数据点进行旋转,旋转至主成分,维度间线性无关。
假设新的坐标为:
F = ( F 1 , F 2 , . . . , F m ) = U T X μ F = ( μ 1 , μ 2 , . . . , μ m ) ( F − μ F ) = U T ( X − μ x ) F = (F_1,F_2,...,F_m) = U^TX \\ \mu_{F} = (\mu_{1}, \mu_{2},...,\mu_{m}) \\ (F-\mu_F)=U^T(X-\mu_x) F=(F1,F2,...,Fm)=UTXμF=(μ1,μ2,...,μm)(F−μF)=UT(X−μx)变换后维度间线性无关且每个维度自己的方差为特征值,所以满足:
( F − μ F ) ( F − μ F ) T = [ λ 1 λ 2 ⋯ λ 4 ] = U T ( X − μ x ) ( X − μ x ) T U = U T Σ X U \begin{aligned} (F-\mu_F)(F-\mu_F)^T&=\left[\begin{array}{llll} \lambda_1 & & & \\ & \lambda_2 & & \\ & & \cdots & \\ & & & \lambda_4 \end{array}\right] \\ &= U^T(X-\mu_x)(X-\mu_x)^TU \\ &= U^T\Sigma_XU \end{aligned} (F−μF)(F−μF)T= λ1λ2⋯λ4 =UT(X−μx)(X−μx)TU=UTΣXU马氏距离是旋转变换缩放后的欧氏距离,所以马氏距离的计算公式为:
D M = ( f 1 − μ F 1 λ 1 ) 2 + ( f 2 − μ F 2 λ 2 ) 2 + … + ( f m − μ F m λ m ) 2 = ( f 1 − μ F 1 , f 2 − μ F 2 , … , f M − μ F M ) [ 1 λ 1 1 λ 2 … 1 λ m ] ( f 1 − μ F 1 f 2 − μ F 2 … f m − μ F m ) = ( f − μ F ) T ( U T Σ X U ) − 1 ( f − μ F ) = ( x − μ X ) T U U T Σ X − 1 U U T ( x − μ X ) = ( x − μ X ) T Σ X − 1 ( x − μ X ) \begin{aligned} D_M & =\left(\frac{f_1-\mu_{F_1}}{\sqrt{\lambda_1}}\right)^2+\left(\frac{f_2-\mu_{F_2}}{\sqrt{\lambda_2}}\right)^2+\ldots+\left(\frac{f_m-\mu_{F_m}}{\sqrt{\lambda_m}}\right)^2 \\ & =\left(f_1-\mu_{F_1}, f_2-\mu_{F_2}, \ldots, f_M-\mu_{F_M}\right)\left[\begin{array}{cccc} \frac{1}{\lambda_1} & & & \\ & \frac{1}{\lambda_2} & & \\ & & \ldots & \\ & & & \frac{1}{\lambda_m} \end{array}\right]\left(\begin{array}{c} f_1-\mu_{F_1} \\ f_2-\mu_{F_2} \\ \ldots \\ f_m-\mu_{F_m} \end{array}\right) \\ & =\left(f-\mu_F\right)^T\left(U^T \Sigma_X U\right)^{-1}\left(f-\mu_F\right) \\ & =\left(x-\mu_X\right)^T U U^T \Sigma_X^{-1} U U^T\left(x-\mu_X\right) \\ & =\left(x-\mu_X\right)^T \Sigma_X^{-1}\left(x-\mu_X\right) \end{aligned} DM=(λ1f1−μF1)2+(λ2f2−μF2)2+…+(λmfm−μFm)2=(f1−μF1,f2−μF2,…,fM−μFM) λ11λ21…λm1 f1−μF1f2−μF2…fm−μFm =(f−μF)T(UTΣXU)−1(f−μF)=(x−μX)TUUTΣX−1UUT(x−μX)=(x−μX)TΣX−1(x−μX)即为之前提到的公式。
5. 马氏距离限制
- 协方差矩阵必须满秩
里面有求逆矩阵的过程,不满秩不行,要求数据要有原维度个特征值,如果没有可以考虑先进行PCA,这种情况下PCA不会损失信息 - 不能处理非线性流形(manifold)上的问题
只对线性空间有效,如果要处理流形,只能在局部定义,可以用来建立KNN图