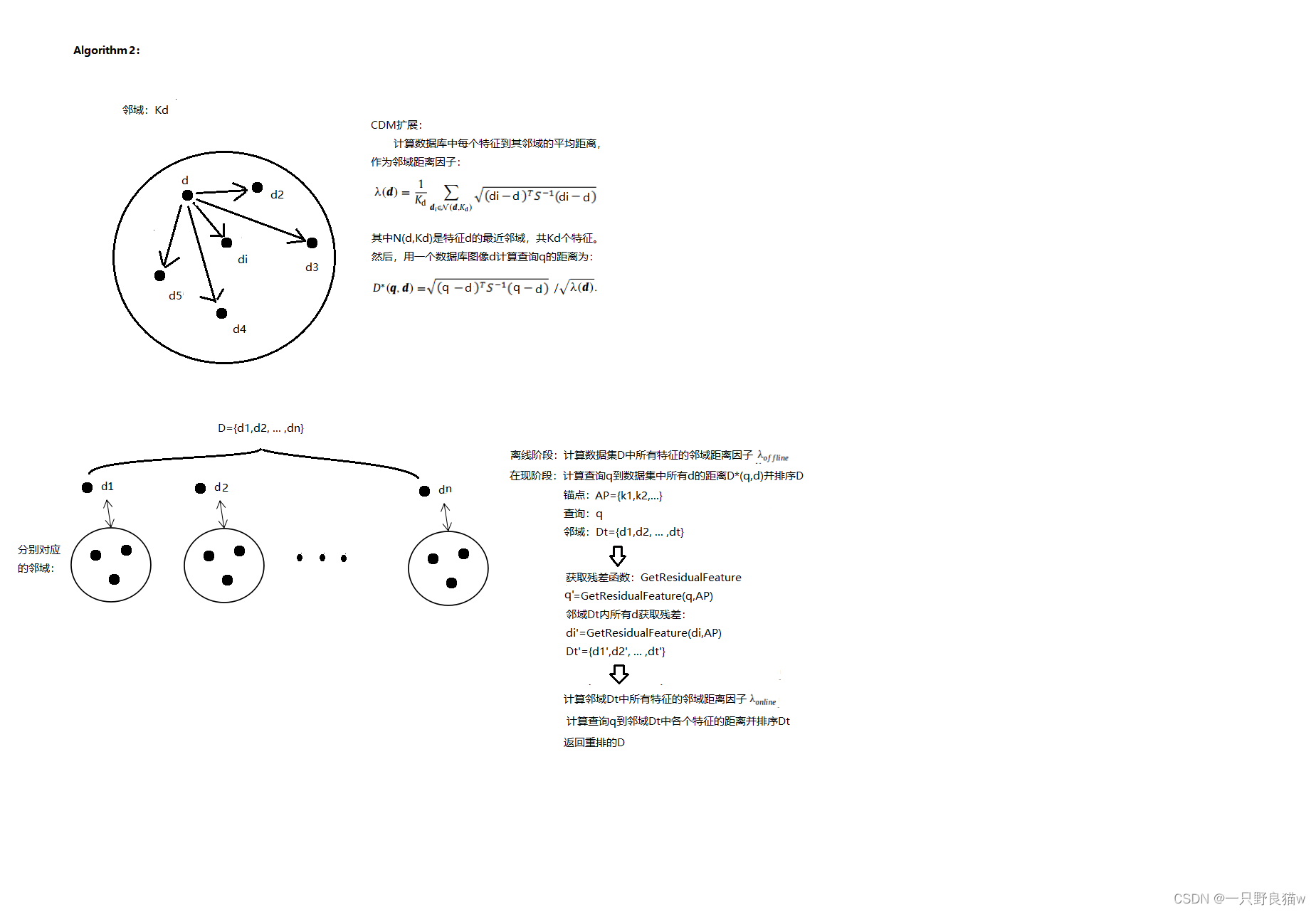
马氏距离例题详解

定义

马哈拉诺比斯距离是由印度统计学家马哈拉诺比斯 (英语)提出的，表示数据的协方差距离。它是一种有效的计算两个未知样本集的相似度的方法。与欧氏距离不同的是它考虑到各种特性之间的联系（例如：一条关于身高的信息会带来一条关于体重的信息，因为两者是有关联的）并且是尺度无关的（scale-invariant），即独立于测量尺度。 对于一个均值为$\mu =({\mu }_1,{\mu }_2,{\mu }_3,\dots ,{\mu }_p{)}^T$，协方差矩阵为$\Sigma$ 的多变量向量$x=(x_1,x_2,x_3,\dots ,x_p{)}^T$，其马氏距离为

$$D_M(x)=\sqrt{(x-\mu {)}^T{\Sigma }^{-1}(x-\mu )}$$
马哈拉诺比斯距离也可以定义为两个服从同一分布并且其协方差矩阵为$\Sigma$的随机变量$\vec{x}$与$\vec{y}$的差异程度：

$$d(\vec{x},\vec{y})=\sqrt{(\vec{x}-\vec{y}{)}^T{\Sigma }^{-1}(\vec{x}-\vec{y})}$$
如果协方差矩阵为单位矩阵，马哈拉诺比斯距离就简化为欧氏距离；如果协方差矩阵为对角阵，其也可称为正规化的欧氏距离。

$$d(\vec{x},\vec{y})=\sqrt{\sum _{i=1}^p\frac{(x_i-y_i{)}^2}{{\sigma }_i^2}}$$
其中${\sigma }_i是x_i$的标准差。

以上引自维基百科

计算示例

问题引入

现在有一组向量：
$$(3,4{)}^T,(5,6{)}^T,(2,2{)}^T,(8,4{)}^T$$
请求出$(3,4{)}^T,(5,6{)}^T$之间的马氏距离。

求解思路

现在将$(3,4{)}^T,(5,6{)}^T,(2,2{)}^T,(8,4{)}^T$四个向量排列：
$$\left[\begin{array}{cccc}3& 5& 2& 8\\ 4& 6& 2& 4\end{array}\right]$$
我们假设$\left[\begin{array}{cccc}3& 5& 2& 8\end{array}\right]$对应的是X，而$\left[\begin{array}{cccc}4& 6& 2& 4\end{array}\right]$对应的是Y。

∵ $\overline{\mathrm{X}}=（3+5+2+8）/4=4.5,\overline{\mathrm{Y}}=(4+6+2+4)/4=4$
∴均值$\vec{\mu }=(4.5,4{)}^T$

然后将$\left[\begin{array}{cccc}3& 5& 2& 8\\ 4& 6& 2& 4\end{array}\right]$中心化，即X中的每个元素减去$\overline{\mathrm{X}}$，Y中的每个元素减去$\overline{\mathrm{Y}}$，得：
$$\left[\begin{array}{cccc}-1.5& 0.5& -2.5& 3.5\\ 0& 2& -2& 0\end{array}\right]$$

$\mathrm{cov}(\mathrm{X},\mathrm{X})=\frac{{\sum }_{\mathrm{i}=1}^4\left({\mathrm{X}}_{\mathrm{i}}-\overline{\mathrm{X}}\right)\left({\mathrm{X}}_{\mathrm{i}}-\overline{\mathrm{X}}\right)}{4-1}=\frac{(-1.5)\times (-1.5)+0.5\times 0.5+(-2.5)\times (-2.5)+3.5\times 3.5}{3}=7$

$\mathrm{cov}(\mathrm{X},\mathrm{Y})=\mathrm{cov}(\mathrm{Y},\mathrm{X})=\frac{{\sum }_{\mathrm{i}=1}^4\left({\mathrm{X}}_{\mathrm{i}}-\overline{\mathrm{X}}\right)\left({\mathrm{Y}}_{\mathrm{i}}-\overline{\mathrm{Y}}\right)}{4-1}=\frac{(-1.5)\times (0)+0.5\times 2+(-2.5)\times (-2)+3.5\times 0}{3}=2$

$\mathrm{cov}(\mathrm{Y},\mathrm{Y})=\frac{{\sum }_{\mathrm{i}=1}^4\left({\mathrm{Y}}_{\mathrm{i}}-\overline{\mathrm{Y}}\right)\left({\mathrm{Y}}_{\mathrm{i}}-\overline{\mathrm{Y}}\right)}{4-1}=\frac{0\times 0+2\times 2+(-2)\times (-2)+0\times 0}{3}=2.667$

$$\therefore 协方差矩阵\Sigma =\left[\begin{array}{cc}7& 2\\ 2& 2.667\end{array}\right]$$
$$\therefore 协方差矩阵的逆{\Sigma }^{-1}=\left[\begin{array}{cc}0.18& -0.13\\ -0.13& 0.48\end{array}\right]$$

$$\therefore 可以计算(3,4{)}^T,(5,6{)}^T之间的距离为：D_M=\sqrt{[(3-5,4-6{)}^T{]}^T{\Sigma }^{-1}(3-5,4-6{)}^T}$$
$$即D_M=\sqrt{(3-5,4-6){\Sigma }^{-1}(3-5,4-6{)}^T}=1.2$$

因此$(3,4{)}^T,(5,6{)}^T$之间的马氏距离为1.2！

代码实现

#coding=utf-8
import numpy
x = numpy.array([[3,4],[5,6],[2,2],[8,4]])
print("x矩阵的维度：",x.ndim)  # 二维向量组成的矩阵
xT = x.T
D = numpy.cov(xT)
invD = numpy.linalg.inv(D)
tp = x[0] - x[1]
print(numpy.sqrt(numpy.dot(numpy.dot(tp, invD), tp.T)))

大功告成！最后感谢小伙伴们的学习噢~