1. Introduction

马氏距离是度量某个点和某个分布间距离的一个指标。在异常值检测、高度不平衡数据的分类以及 one-class 分类上都有着广泛的应用。本文将解释马氏距离背后的intuition以及用一些实例帮助大家更好地理解这个指标。

2. 欧式距离对于多元数据会存在一些什么问题？

在介绍马氏距离之前，我想有必要对欧式距离进行一些简单的阐述。欧式距离是我们衡量两个点之间距离的最常用的指标。
如果两个点在一个二维平面中，那么对于这两个点 (p1,q1) 和 (p2,q2) 之间的欧式距离可以表示为：

对于多维空间，上述式子可以拓展为：

当然，只要维数（列）equally weighted并且相互独立，欧式距离仍是不错的选择。
这句话是什么意思呢，接下来举个例子。

这两个表显示了相同对象的“Area”和“Price”，仅仅是变量的单位发生了改变。理论上，任意两行（可以理解为A点和B点）之间的距离都是相同的，但是欧式距离计算的话就会产生不同的值。当然，这个问题可以从技术上加以克服，比如对它进行标准化处理（(x – mean) / std），使其范围在0到1之间。

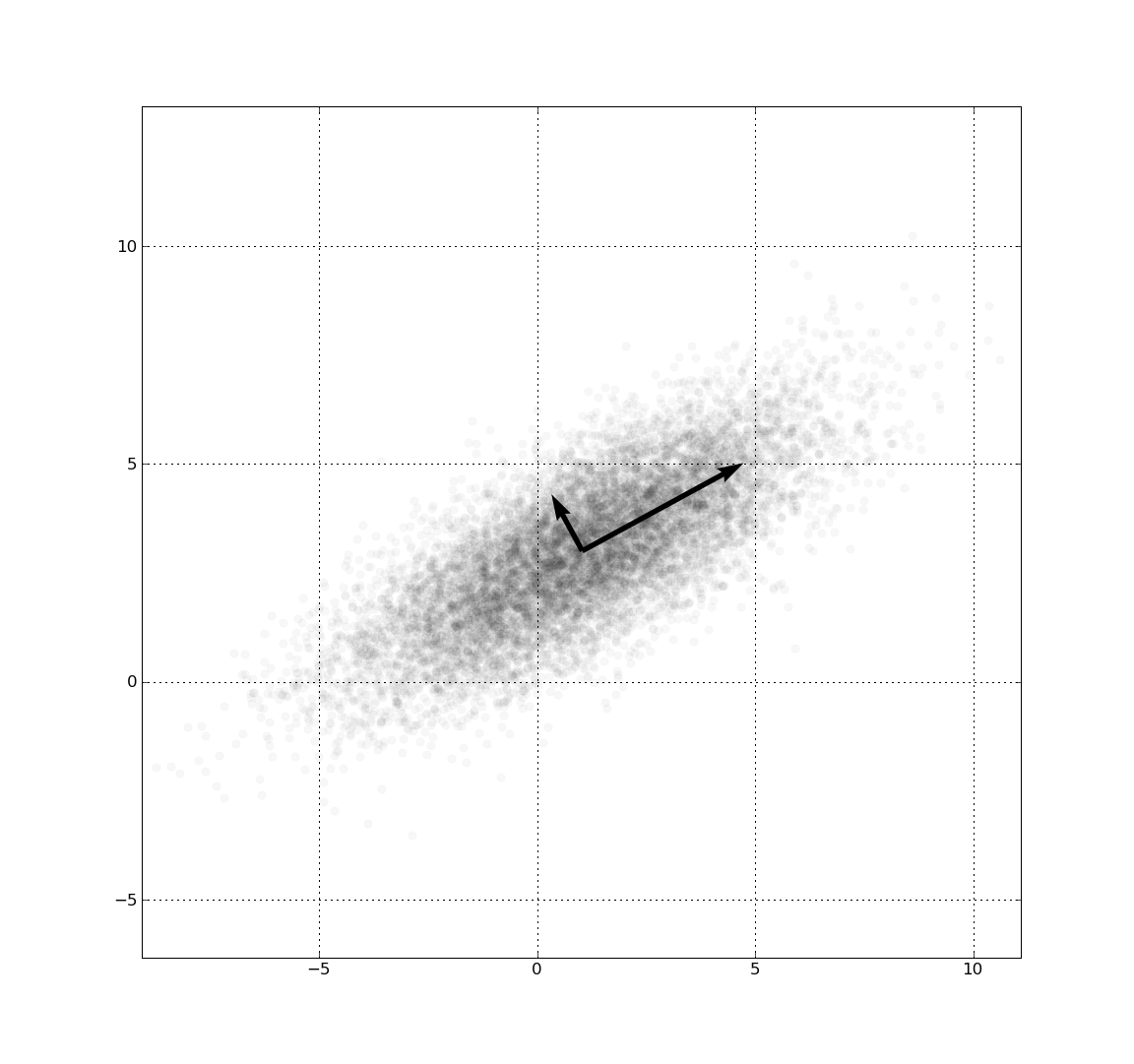
但是，欧式距离还有一个缺点。如果维度（数据集中的列）相互关联（这在实际数据集中通常是这种情况），那么点和分布间的欧式距离对于这个点到底离分布多近就会给出一些误导信息。

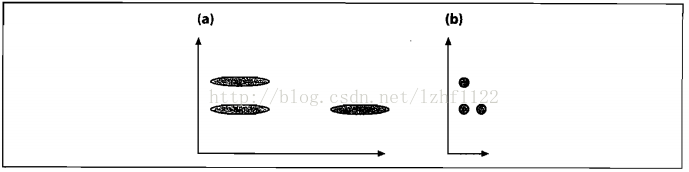
右上图给出了两个正相关变量的散点图。当一个变量增加时，另一个变量也会增加。图中蓝点和红点与中心的（欧式）距离相等，但实际上只有蓝色才是更接近cluster的。

这是因为，欧式距离刻画的仅仅是两个点之间的距离，它并不考虑数据集中的其余点是如何变化的。因此，欧式距离是不能用来真正的判断一个点与点的分布到底有多接近的。

这就引入了马氏距离。

3 .什么是马氏距离

马氏距离是点和分布间点距离，并不是两个点之间的距离，它其实是欧式距离的多元等效项。

那么在计算上，马氏距离到底与欧式距离有何不同呢？

（1） 它将“列”转化成不相关的向量。
（2） 缩放列使其方差等于1。
（3） 最后计算欧式距离

这三个步骤很好地解决了刚才所谈的关于欧式距离的一些缺点。接下来我们来详细了解一下马氏距离。

4.马氏距离背后的数学和intuition

首先，奉上马氏距离的公式：

这里，D^2 即为马氏距离；x表示观察到的向量（数据集的row）；m表示独立变量（列）的均值向量；C^(-1)表示的是独立变量协方差矩阵的逆。

scale
(x-m)实际上是向量与均值的距离，然后除以协方差矩阵。这个形式有没有很眼熟？这实际上是标准化的多元等价形式。z = (x vector) - (mean vector) / (covariance matrix)

correlation
那除以协方差有什么作用呢？

如果数据集中的变量是高度相关的，那么会导致协方差很大，除以较大的协方差就可以有效地减小距离。那如果X并不相关，那么协方差也不大，因此距离也不会减小很多。

综上所述，马氏距离可以有效地解决欧式距离的量纲和相关性的问题。

5. 利用python来计算马氏距离

import pandas as pd
import scipy as sp
import numpy as npfilepath = 'https://raw.githubusercontent.com/selva86/datasets/master/diamonds.csv'
df = pd.read_csv(filepath).iloc[:, [0,4,6]]
df.head()

接下来写计算马氏距离的公式。

def mahalanobis(x=None, data=None, cov=None):"""Compute the Mahalanobis Distance between each row of x and the data  x    : vector or matrix of data with, say, p columns.data : ndarray of the distribution from which Mahalanobis distance of each observation of x is to be computed.cov  : covariance matrix (p x p) of the distribution. If None, will be computed from data."""x_minus_mu = x - np.mean(data)if not cov:cov = np.cov(data.values.T)inv_covmat = sp.linalg.inv(cov)left_term = np.dot(x_minus_mu, inv_covmat)mahal = np.dot(left_term, x_minus_mu.T)return mahal.diagonal()df_x = df[['carat', 'depth', 'price']].head(500)
df_x['mahala'] = mahalanobis(x=df_x, data=df[['carat', 'depth', 'price']])
df_x.head()

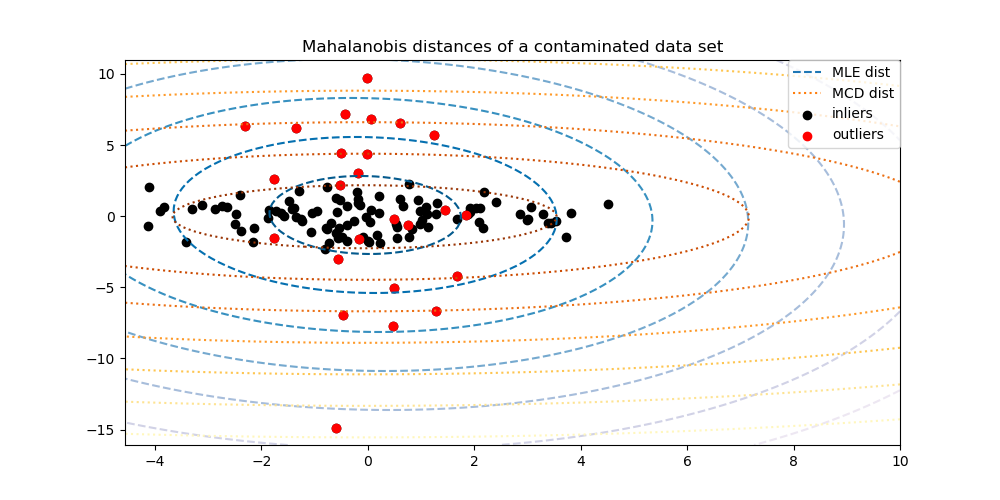
6. Case1: 使用马氏距离进行多元异常值检测

假设检验统计量遵循自由度为n的卡方分布，则在0.01显著性水平和2自由度下的临界值计算如下：

# Critical values for two degrees of freedom
from scipy.stats import chi2
chi2.ppf((1-0.01), df=2)
#> 9.21

这意味着，如果观测值的马氏距离超过9.21，则可以认为是极端。

当然也可以用p值来确定观察值是否极端：

# Compute the P-Values
df_x['p_value'] = 1 - chi2.cdf(df_x['mahala'], 2)# Extreme values with a significance level of 0.01
df_x.loc[df_x.p_value < 0.01].head(10)

这些值和数据集中的其余部分进行比较，那很显然是极端的。

7. Case 2: 对分类问题应用马氏距离

利用马氏距离进行分类的intuition是将观察值归类为与它最接近的类别。

让我们看一下BreastCancer数据集上的示例实现，其目的是确定肿瘤是良性还是恶性的。

df = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/BreastCancer.csv', usecols=['Cl.thickness', 'Cell.size', 'Marg.adhesion', 'Epith.c.size', 'Bare.nuclei', 'Bl.cromatin', 'Normal.nucleoli', 'Mitoses', 'Class'])df.dropna(inplace=True)  # drop missing values.
df.head()

让我们以70:30的比例将数据集拆分为训练和测试。然后将训练数据集分为“ pos”（1）和“ neg”（0）类的同类组。为了预测测试数据集的类别，我们测量给定观测值（行）与正值（xtrain_pos）和负值数据集（xtrain_neg）之间的马氏距离。然后，根据观察到的最接近的组为其分配类别。

from sklearn.model_selection import train_test_split
xtrain, xtest, ytrain, ytest = train_test_split(df.drop('Class', axis=1), df['Class'], test_size=.3, random_state=100)# Split the training data as pos and neg
xtrain_pos = xtrain.loc[ytrain == 1, :]
xtrain_neg = xtrain.loc[ytrain == 0, :]

接下来构建Mahalanobis Binary Classifier。

class MahalanobisBinaryClassifier():def __init__(self, xtrain, ytrain):self.xtrain_pos = xtrain.loc[ytrain == 1, :]self.xtrain_neg = xtrain.loc[ytrain == 0, :]def predict_proba(self, xtest):pos_neg_dists = [(p,n) for p, n in zip(mahalanobis(xtest, self.xtrain_pos), mahalanobis(xtest, self.xtrain_neg))]return np.array([(1-n/(p+n), 1-p/(p+n)) for p,n in pos_neg_dists])def predict(self, xtest):return np.array([np.argmax(row) for row in self.predict_proba(xtest)])clf = MahalanobisBinaryClassifier(xtrain, ytrain)        
pred_probs = clf.predict_proba(xtest)
pred_class = clf.predict(xtest)# Pred and Truth
pred_actuals = pd.DataFrame([(pred, act) for pred, act in zip(pred_class, ytest)], columns=['pred', 'true'])
print(pred_actuals[:5])     

输出：

让我们看看分类器如何在测试数据集上执行。

from sklearn.metrics import classification_report, accuracy_score, roc_auc_score, confusion_matrix
truth = pred_actuals.loc[:, 'true']
pred = pred_actuals.loc[:, 'pred']
scores = np.array(pred_probs)[:, 1]
print('AUROC: ', roc_auc_score(truth, scores))
print('\nConfusion Matrix: \n', confusion_matrix(truth, pred))
print('\nAccuracy Score: ', accuracy_score(truth, pred))
print('\nClassification Report: \n', classification_report(truth, pred))

输出：

AUROC:  0.9909743589743589Confusion Matrix: [[113  17][  0  75]]Accuracy Score:  0.9170731707317074Classification Report: precision    recall  f1-score   support0       1.00      0.87      0.93       1301       0.82      1.00      0.90        75avg / total       0.93      0.92      0.92       205

8. Case 3: one-class classification

One-class是一种算法，其中训练数据集包含仅属于一个类的观察值。在仅知道该信息的情况下，目标是确定新（或测试）数据集中的给定观察是否属于该类。

让我们在BreastCancer数据集上尝试一下，我们将仅考虑训练数据中的恶性观察（类别column = 1）。

df = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/BreastCancer.csv', usecols=['Cl.thickness', 'Cell.size', 'Marg.adhesion', 'Epith.c.size', 'Bare.nuclei', 'Bl.cromatin', 'Normal.nucleoli', 'Mitoses', 'Class'])df.dropna(inplace=True)  # drop missing values.

将数据集的50％分成训练和测试。训练数据中仅保留1。

from sklearn.model_selection import train_test_split
xtrain, xtest, ytrain, ytest = train_test_split(df.drop('Class', axis=1), df['Class'], test_size=.5, random_state=100)# Split the training data as pos and neg
xtrain_pos = xtrain.loc[ytrain == 1, :]

让我们构建一个，MahalanobisOneClassClassifier并从训练集（xtrain_pos）中获得x中每个数据点的马氏距离。

class MahalanobisOneclassClassifier():def __init__(self, xtrain, significance_level=0.01):self.xtrain = xtrainself.critical_value = chi2.ppf((1-significance_level), df=xtrain.shape[1]-1)print('Critical value is: ', self.critical_value)def predict_proba(self, xtest):mahalanobis_dist = mahalanobis(xtest, self.xtrain)self.pvalues = 1 - chi2.cdf(mahalanobis_dist, 2)return mahalanobis_distdef predict(self, xtest):return np.array([int(i) for i in self.predict_proba(xtest) > self.critical_value])clf = MahalanobisOneclassClassifier(xtrain_pos, significance_level=0.05)
mahalanobis_dist = clf.predict_proba(xtest)# Pred and Truth
mdist_actuals = pd.DataFrame([(m, act) for m, act in zip(mahalanobis_dist, ytest)], columns=['mahal', 'true_class'])
print(mdist_actuals[:5])            

Critical value is:  14.067140449340169mahal  true_class
0  13.104716           0
1  14.408570           1
2  14.932236           0
3  14.588622           0
4  15.471064           0

我们有马氏距离和每个观测的实际类别。我希望那些具有低马氏距离的观测值是1。因此，我mdist_actuals按Mahalanobis距离进行排序，并按分位数将行分成10个相等大小的组。顶部分位数中的观察数应比底部分位数中的观察数多。让我们来看一下。

# quantile cut in 10 pieces
mdist_actuals['quantile'] = pd.qcut(mdist_actuals['mahal'], q=[0, .10, .20, .3, .4, .5, .6, .7, .8, .9, 1], labels=[1, 2, 3, 4, 5, 6, 7, 8, 9, 10])# sort by mahalanobis distance
mdist_actuals.sort_values('mahal', inplace=True)
perc_truths = mdist_actuals.groupby('quantile').agg({'mahal': np.mean, 'true_class': np.sum}).rename(columns={'mahal':'avg_mahaldist', 'true_class':'sum_of_trueclass'})
print(perc_truths)

avg_mahaldist  sum_of_trueclass
quantile                                 
1              3.765496                33
2              6.511026                32
3              9.272944                30
4             12.209504                20
5             14.455050                 4
6             15.684493                 4
7             17.368633                 3
8             18.840714                 1
9             21.533159                 2
10            23.524055                 1

1（恶性病例）中将近90％落在马氏距离的前40％范围内。顺便提及，所有这些都低于临界值pf 14.05。因此，让我们将临界值作为临界值，并将那些马氏距离小于临界值的观测值标记为正值。

from sklearn.metrics import classification_report, accuracy_score, roc_auc_score, confusion_matrix# Positive if mahalanobis 
pred_actuals = pd.DataFrame([(int(p), y) for y, p in zip(ytest, clf.predict_proba(xtest) < clf.critical_value)], columns=['pred', 'true'])# Accuracy Metrics
truth = pred_actuals.loc[:, 'true']
pred = pred_actuals.loc[:, 'pred']
print('\nConfusion Matrix: \n', confusion_matrix(truth, pred))
print('\nAccuracy Score: ', accuracy_score(truth, pred))
print('\nClassification Report: \n', classification_report(truth, pred))

Confusion Matrix: [[183  29][ 15 115]]Accuracy Score:  0.8713450292397661Classification Report: precision    recall  f1-score   support0       0.92      0.86      0.89       2121       0.80      0.88      0.84       130avg / total       0.88      0.87      0.87       342

因此，在不了解良性分类的情况下，我们能够准确预测87％的观察结果的分类。

结论

在这篇文章中，几乎涵盖了有关马氏距离的所有内容：公式背后的intuition，python中的实际计算以及如何将其用于多元异常检测，二进制分类和一类分类。