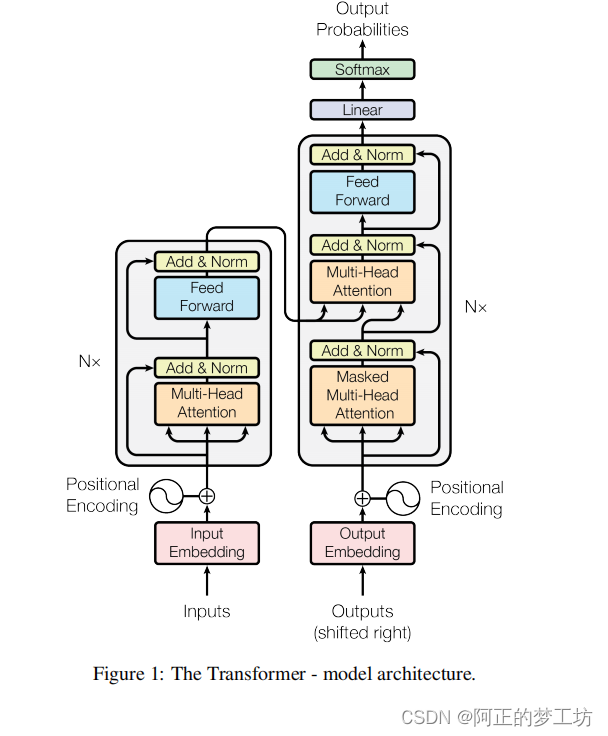
本质

1. 基于消息的流水线处理模型
2. 是一套类似MapReduce一样的编程模型
3. 内核是一套调度系统

适合的业务

1. 高并发的计算任务
2. 数据流之间相互无依赖

编程模型

1. Topology：即一个数据流的拓扑结构，包含多个Spout和Bolt
2. Spout：从外部获取数据，包含DB，Hbase，Kafka等
3. Bolt ：计算单元，系统内计算流转数据
   

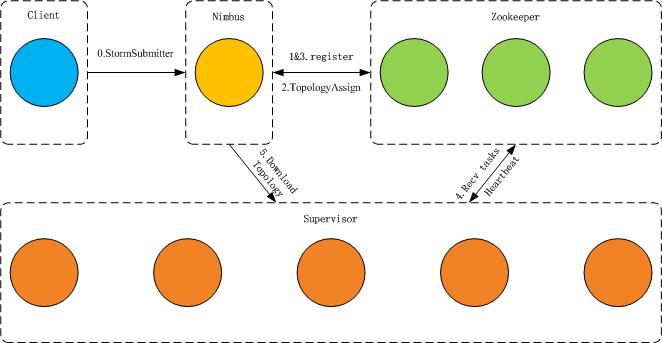
角色

1. Nimbus： 资源调度角色，可主备
2. Supervisor： 接受nimubs 任务安排，启动任务，管理Worker
3. Worker： 进程
4. Executor： 执行线程,继承自Runnable
5. Task： 执行逻辑单元,继承自Runnable

ack机制

ack闭环，保证数据不丢失（以后会结合源码分析ack实现）

1. 设置acker 的并行个数，如果设置为0,acker失效，不能保证数据不丢失,或者设置配置topology.acker.executors（默认为null，即与该任务的work数一致）

   stormConf.setNumAckers(JStormUtils.parseInt(conf.getProperty("jstorm.acker.num")));

2. Spout 发送消息必须带msgId，否则不能实现acker闭环

   collector.emit(new Values(strMsg), new KafkaMessageId(partition, toEmitMsg.offset()));

3. Bolt发送消息必须传入接收到的tuple作为anchors参数的值，这样才能锚定tuple，将此Bolt纳入Ack闭环中

       public List<Integer> emit(String streamId, Collection<Tuple> anchors,List<Object> tuple)

4. topology.max.spout.pending设置，默认为null，无限。对spout task接收速度进行流控。当topology.max.spout.pending=5000,对于spout而言，还有5000个没有进行ack，就会停止spout的nextTuple。

   topology.max.spout.pending设置后，会降低整个系统的吞吐量，可根据自己系统要求自行设置，以先某个数值开始，不断增加，最终达到系统稳定且吞吐量合适

   topology.max.spout.pending要起作用，必须锚定tuple，因为这个是在ack闭环的基础上实现的。所以必须满足条件1,2,3

5. spout发送的事件在超时时间(topology.message.timeout.secs 默认为30s)内没有最终ack闭环，系统就会自动调用spout.fail,由spout编写者自行处理，一般在里面实现重传，如果实现不好，或者不处理，数据也会丢失

6. acker闭环并不保证数据不丢失，只是提供了一个机制可以实现数据不丢失，取决于Spout的编写者。acker闭环完成会调用spout.ack,闭环失败或者超时会调用 spout.fail