看了一些博客对马氏距离的解释,似乎没有讲到本质的地方,本文从欧氏距离存在的问题开始入手,一步步推导出马氏距离,并得出结论:原始空间中的马氏距离等于坐标旋转变换及缩放后的空间中的欧氏距离。
假设数据集 X ∈ R N × F X\in R^{N\times F} X∈RN×F, x 1 , x 2 ∈ R F x_1,x_2\in R^{F} x1,x2∈RF为数据集中的两个样本,则 x 1 x_1 x1与 x 2 x_2 x2的马氏距离是
D i s m a h a l a n o b i s ( x 1 , x 2 ) = ( x 1 − x 2 ) Σ − 1 ( x 1 − x 2 ) T Dis_{mahalanobis}(x_1,x_2)=\sqrt{(x_1-x_2)\Sigma^{-1}(x_1-x_2)^T} Dismahalanobis(x1,x2)=(x1−x2)Σ−1(x1−x2)T
其中Σ是X的协方差矩阵。与欧式距离的最大区别是公式中多了协方差矩阵的逆 Σ − 1 Σ^{-1} Σ−1,它的作用是:排除变量之间相关性的干扰,并且排除测量量纲的影响。下面推导马氏距离的公式由来及 Σ − 1 Σ^{-1} Σ−1的物理意义。
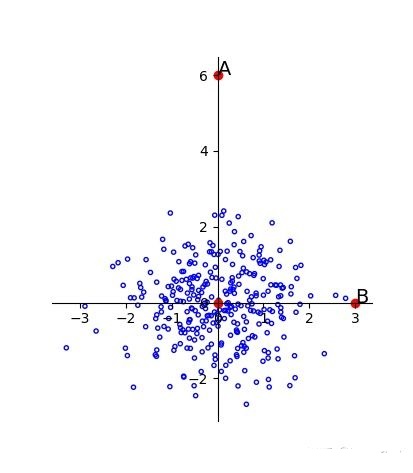
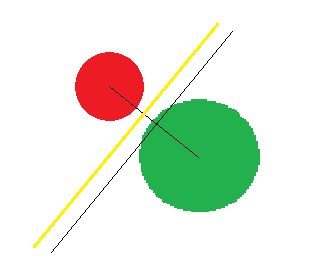
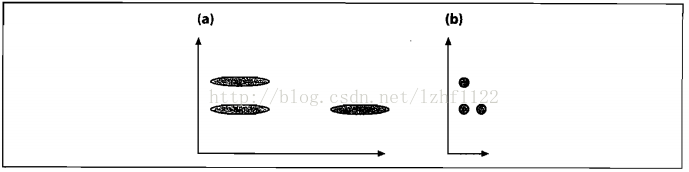
问题引入:考虑图1所示二维数据集,可以发现两个维度间存在很强的相关性,其中红点和绿点到中心点(黑点)的欧式距离是一样的,但是从图中可以发现,红点更像是异常点,因此这种情况下用欧氏距离来判断效果不好。而马氏距离通过将数据进行坐标旋转、缩放到另一个空间后可以直接使用欧氏距离区分开红点和绿点。

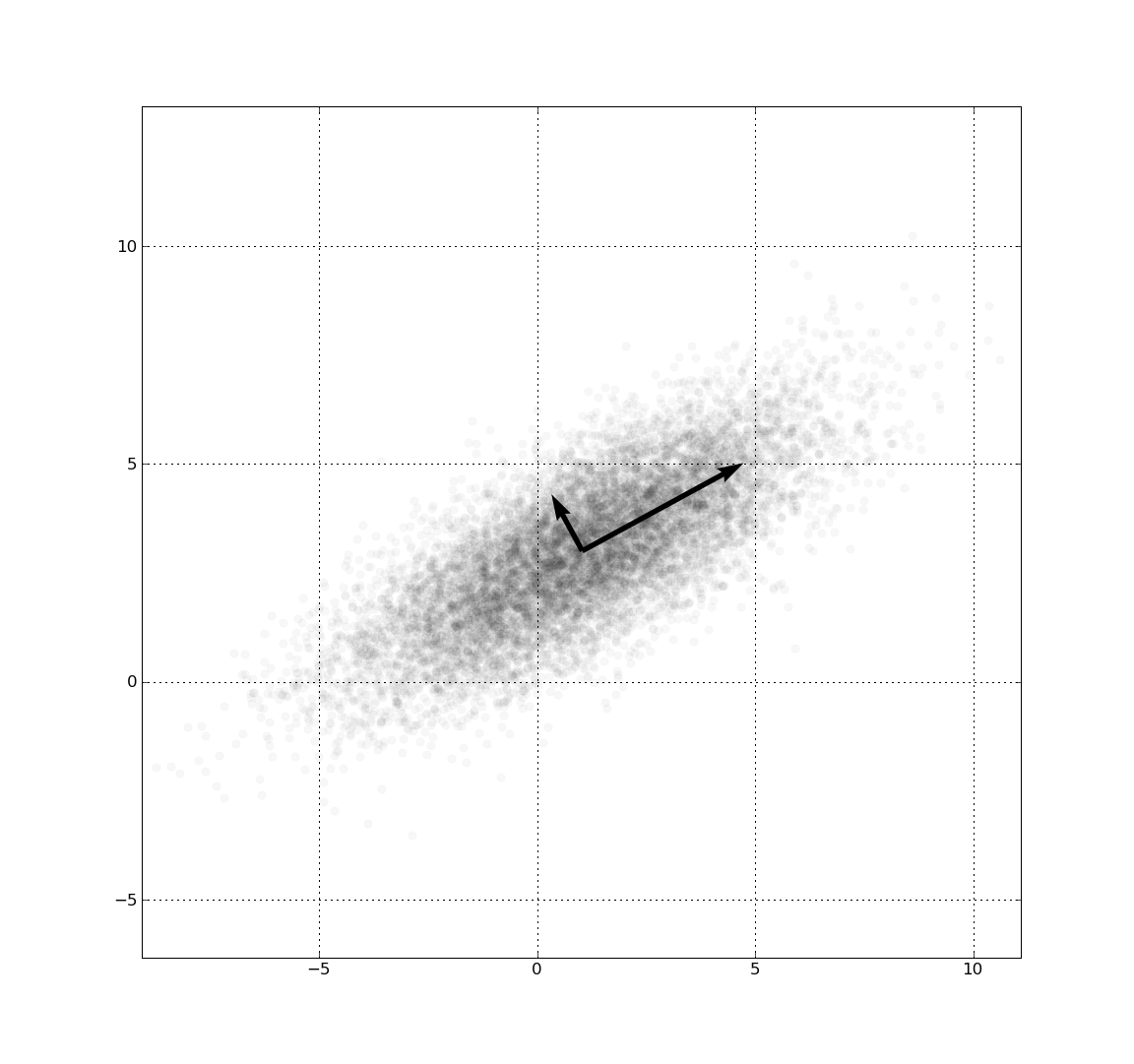
- 消除相关性(坐标旋转): 首先考虑消除各个维度之间的相关性。这里需要一些PCA算法的基础知识,如果了解PCA算法就会知道PCA降维后各个维度间是独立的,而PCA本质上就是对数据集进行坐标旋转,旋转后就消除了各个维度之间的相关性。PCA对数据集X的协方差矩阵Σ进行特征分解 Σ = U T Q U Σ=U^T QU Σ=UTQU,U是特征向量组成的矩阵,并且是一个正交矩阵(即 U T U = I U^T U=I UTU=I,因为Σ是实对称的,所以正交),即U是一组正交基组成的矩阵,随后PCA将数据集X投影到这组正交基上便消除了各维度间的相关性,PCA会取前k个维度来达到降维的目的,但这里我们不降维,因此保留所有维度直接投影到U上即可,投影和旋转变换是一样的意思,投影的方法是将数据集乘以基矩阵U(矩阵相乘实际上就是一种坐标变换),得到消除相关性后的数据集Y Y = X U Y=XU Y=XU

- 排除量纲影响(缩放): 如图2所示,可以看到坐标旋转变换后两个维度之间相关性已经很小了,但是样本之间的相对位置不变,红点和绿点到黑点的欧氏距离还是一样,仍然无法区分开,此时还需要进行缩放处理,从图2可以看到数据在横向的方差比较大,而在纵向的方差比较小,这会造成量纲的不统一,例如现在有两个类别,第一个类别均值为0,方差为0.1,第二个类别均值为5,方差为5。那么一个值为2的点属于第一类的概率大还是第二类的概率大?距离上说应该是第一类,但是直觉上显然是第二类,因为第一类不太可能到达2这个位置(参考)。因此还需要对每个维度进行缩放,即每个维度除以对应维度的标准差(为了跟马氏距离的公式对上应该是除以标准差而不是方差),这里的标准差是Y每个维度的标准差而不是X。假设σ_i 是第i个维度的方差,Z是缩放后的数据集,则

如图3所示为Y进行缩放后的数据集,可以看到此时就可以直接用欧氏距离把红点和绿点区分开了。

通过以上分析就可以推导马氏距离的公式了,设 z 1 , z 2 ∈ R F z_1,z_2∈R^F z1,z2∈RF是Z中的两个样本,则 z 1 z_1 z1与 z 2 z_2 z2的欧式距离是
D i s E u c l i d e a n ( z 1 , z 2 ) = ( z 1 − z 2 ) ( z 1 − z 2 ) T = ( y 1 Λ − y 2 Λ ) ( y 1 Λ − y 2 Λ ) T = ( x 1 U Λ − x 2 U Λ ) ( x 1 U Λ − x 2 U Λ ) T = ( x 1 − x 2 ) U Λ Λ U T ( x 1 − x 2 ) T = ( x 1 − x 2 ) Σ − 1 ( x 1 − x 2 ) T ( 这 个 等 号 推 导 见 下 方 ) = D i s m a h a l a n o b i s ( x 1 , x 2 ) \begin{aligned} Dis_{Euclidean}(z_1,z_2)&=\sqrt{(z_1-z_2)(z_1-z_2)^T} \\ &=\sqrt{(y_1\Lambda-y_2\Lambda)(y_1\Lambda-y_2\Lambda)^T}\\ &=\sqrt{(x_1U\Lambda-x_2U\Lambda)(x_1U\Lambda-x_2U\Lambda)^T}\\ &=\sqrt{(x_1-x_2)U\Lambda\Lambda U^T(x_1-x_2)^T}\\ &=\sqrt{(x_1-x_2)\Sigma^{-1}(x_1-x_2)^T} (这个等号推导见下方)\\ &=Dis_{mahalanobis}(x_1,x_2) \end{aligned} DisEuclidean(z1,z2)=(z1−z2)(z1−z2)T=(y1Λ−y2Λ)(y1Λ−y2Λ)T=(x1UΛ−x2UΛ)(x1UΛ−x2UΛ)T=(x1−x2)UΛΛUT(x1−x2)T=(x1−x2)Σ−1(x1−x2)T(这个等号推导见下方)=Dismahalanobis(x1,x2)
懒得打公式了,直接截图上来吧,上面那个等号的推导

也就是说在原始空间中的马氏距离等于坐标旋转变换及缩放后的空间中的欧氏距离, Σ − 1 Σ^{-1} Σ−1的作用就是对数据进行坐标旋转和缩放。整个过程见下图

实验代码
from scipy.spatial.distance import pdist
from numpy import array, cov, diag, mean, sqrt, vstack
from numpy.random import multivariate_normal
from numpy.linalg import eig
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt"""生成二维正太分布数据`X` 两个维度间的协方差为0.8(强相关).
在X的尾部加入点A和点B,点B属于数据集X而点A为异常点,且点A和B到原点(0,0)的`欧式距离`相等.
本次实验旨在通过坐标旋转和缩放后通过欧式距离将点A和B区分开,理解马氏距离中sigma的物理意义."""
N = 4 # 数据集大小
X = multivariate_normal(mean=[0, 0],size=N,cov=[[1, 0.8],[0.8, 1]])point_A = array([-3, 2]) # 异常点
point_B = array([3, 2])# 添加点A和B到尾部
X = vstack((X, point_A))
X = vstack((X, point_B))# 旋转
Q, U = eig(cov(X, rowvar=False))
Y = X.dot(U)
# 缩放
Cov_Y = cov(Y, rowvar=False) # 求Y的协方差矩阵
diag_Y = diag([sqrt(1/Cov_Y[i][i]) for i in range(len(Cov_Y))]) # 取协方差矩阵对角线元素的倒数
Z = Y.dot(diag_Y) # 缩放后的特征print(pdist(X, 'mahalanobis')) # 原始数据X的马氏距离
print(pdist(Z)) # 旋转缩放后的欧氏距离def plot_point(data, N, plt_temp):plt_temp.scatter(data[:N, 0], data[:N, 1], c='b')plt_temp.scatter(data[N, 0], data[N, 1], c='r') # 点Aplt_temp.scatter(data[N+1, 0], data[N+1, 1], c='g')plt_temp.scatter(0, 0, c='k') # 原点plt_temp.xlim([-8, 8])plt_temp.ylim([-8, 8])return plt_tempplt.subplot(1, 3, 1)
plt = plot_point(X, N, plt)
plt.subplot(1, 3, 2)
plt = plot_point(Y, N, plt)
plt.subplot(1, 3, 3)
plt = plot_point(Z, N, plt)
plt.show()