一、SVD简介
Singular Value Decomposition(奇异值分解,SVD)是一种重要的矩阵分解技术,可以将一个矩阵分解为三个矩阵的乘积。SVD的应用广泛,包括数据降维、矩阵逆运算、推荐系统等领域。
给定一个矩阵A,SVD将其分解为以下形式:
A = UΣV^T
其中,U和V是正交矩阵,Σ是对角矩阵。U的列向量称为左奇异向量,V的列向量称为右奇异向量。Σ的对角元素称为奇异值,通常按降序排列。在SVD中,奇异值代表原始矩阵的重要性,奇异值较大的对应的左右奇异向量所表示的特征对数据的贡献较大。
SVD的应用中,常用到SVD的截断形式。通过保留较大的奇异值和对应的奇异向量,可以实现数据降维,提取出数据的主要特征。
总的来说,SVD是一种强大的矩阵分解技术,可以在数据处理和分析中发挥重要作用,尤其在降维和特征提取方面。
二、特征值和特征向量
在线性代数中,特征值和特征向量是矩阵的重要性质。对于一个n×n的方阵A,如果存在一个非零向量v和一个实数λ,满足 Av = λv,那么λ称为A的特征值,v称为对应于特征值λ的特征向量。特征向量是指在线性变换过程中,只发生拉伸或压缩,方向不发生改变的向量。特征值表示特征向量在该线性变换中的缩放比例。
特征值和特征向量的性质包括:
1. 每个n×n矩阵至少有一个特征值和相应的特征向量(可以是复数)。
2. 特征向量可以乘以一个非零常数而不改变关系。
3. 特征向量对应的特征值不一定唯一,但是特征向量的方向是唯一确定的。
4. 特征值的个数不超过矩阵的维度n。
特征值和特征向量在多个领域有广泛应用,包括线性代数、物理学、工程学、数据分析等。在数据分析中,特征值和特征向量常用于降维、特征提取、主成分分析等任务,以帮助理解和处理数据。我们首先回顾下特征值和特征向量的定义如下:
Ax=λx
给定一个n×n的矩阵A和一个n维向量x,如果存在一个实数λ,使得Ax = λx成立,那么λ被称为矩阵A的特征值,而x称为对应于特征值λ的特征向量。特征值和特征向量的定义表示,在矩阵A作用下,特征向量x只发生缩放而不改变方向,缩放比例由特征值λ决定。
求出特征值和特征向量有什么好处呢?就是我们可以将矩阵A特征分解。如果我们求出了矩阵A的n个特征值λ1≤λ2 <...≤λn,以及这n个特征值所对应的特征向量{w1, w2,... wn},那么矩阵A就可以用下式的特征分解表示:

其中W是这n个特征向量所张成的n X n维矩阵,而Σ为这n个特征值为主对角线的n X n维矩阵。
一般我们会把W的这n 个特征向量标准化,即满足||wi||2 = 1,或者说wi.Twi = 1,此时W的n个特征向量为标准正交基,满足W.TW = 1,即W.T = w-1,也就是说W为酉矩阵。
这样我们的特征分解表达式可以写成:

特征值分解只可以在方阵中进行处理,不能应用的非方阵中,如果我们要对非方阵进行特征分解,这是我们就要用到SVD。
三、SVD的定义
SVD也是对矩阵进行分解,但是和特征分解不同,SVD并不要求矩阵为方阵。假设我们的矩阵A是一个m×n的矩阵,那么我们定义矩阵A的SVD为:

在SVD中,U是一个m×m的酉矩阵,Σ是一个m×n的矩阵,除了主对角线上的元素以外全为零,主对角线上的每个元素都称为奇异值,V是一个n×n的酉矩阵。酉矩阵是指其转置矩阵乘以自身得到单位矩阵,即U^TU = I,V^TV = I。下图可以很形象的看出上面SVD的定义:

四、求解SVD矩阵
那么我们如何求出SVD分解后的U, Σ,V这三个矩阵呢?
如果我们将A的转置和A做矩阵乘法,那么会得到n X n的一个方阵AT A。既然AT A是方阵,那么我们就可以进行特征分解,得到的特征值和特征向量满足下式:
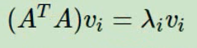
是的,通过对矩阵A的转置矩阵AT与A相乘得到的矩阵AT A,我们可以求解出其n个特征值和对应的n个特征向量v。将AT A的所有特征向量组成一个n×n的矩阵V,这个V矩阵即可作为SVD公式中的V。
如果我们将A和A的转置做矩阵乘法,那么会得到m x m的一一个方阵AAT。 既然AAT是方阵,那么我们就可以进行特征分解,得到的特征值和特征向量满足下式:
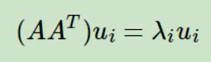
这样我们就可以得到矩阵AAT的m个特征值和对应的m个特征向量u了。将AAT的所有特征向量张成一个m x m的矩阵U ,就是我们SVD公式里面的U矩阵了。-般我们将U中的每个特征向量叫做A的左奇异向量。
U和V我们都求出来了, 现在就剩下奇异值矩阵习没有求出了。由于乙除了对角线上是奇异值其他位置都是0 ,那我们只需要求出每个奇异值σ就可以了。

这样我们可以求出每个奇异值,进而求出奇异矩阵。
在上述中为什么A*A.T为U矩阵,而A.T*A为V矩阵?
原因如下:

进一步我们还可以看出我们的特征值矩阵等于奇异值矩阵的平方,也就是说特征值和奇异值满足如下关系:
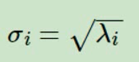
这样也就是说,我们可以不用σi = Avi/u;来计算奇异值,也可以通过求出AT A的特征值取平方根来求奇异值。(奇异矩阵是从大到小排序)
五、求解实例



六、SVD性质
对于奇异值,它跟我们特征分解中的特征值类似,在奇异值矩阵中也是按照从大到小排列,而且奇异值的减少特别的快,在很多情况下,前10%甚至1 %的奇异值的和就占了全部的奇异值之和的99%以上的比例。也就是说,我们也可以用最大的k个的奇异值和对应的左右奇异向量来近似描述矩阵。
由于这个重要的性质,SVD可以用于PCA降维,来做数据压缩和去噪。也可以用于推荐算法,将用户和喜好对应的矩阵做特征分解,进而得到隐含的用户需求来做推荐。同时也可以用于NLP中的算法,比如潜在语义索引(LSI) 。
七、SVD用于PCA降维
实际上SVD在PCA降维上只是使用了V矩阵(右奇异矩阵),其原因就是V矩阵(右奇异矩阵)是进行列压缩,而U矩阵(左奇异矩阵)是对行进行压缩,而PCA降维只需要减少特征从而进行降维,所以PCA只用到了SVD的V矩阵(右奇异矩阵)。具体解释可参照上文推导过程(右奇异矩阵的由来)。
八、SVD总结
SVD作为一种基本算法,在许多机器学习算法中都扮演重要角色。特别是在大数据时代,SVD因其可并行化的特性而更加广泛应用。SVD的原理并不复杂,只需要基本的线性代数知识即可理解,实现也相对简单,因此值得仔细研究。
然而,SVD的一个缺点是其分解出的矩阵在解释性方面较弱,有时候更像是一个黑盒子。尽管如此,这并不影响SVD在实际应用中的使用。SVD在数据处理、降维、特征提取等领域都发挥了重要作用。
需要注意的是,在使用SVD时,我们也要考虑到其计算复杂度的问题,特别是对于大规模矩阵的处理。尽管SVD具有许多优点,但在实际应用中,我们也需要综合考虑算法的效率和性能,选择适合特定任务的算法和技术。