红黑树的定义

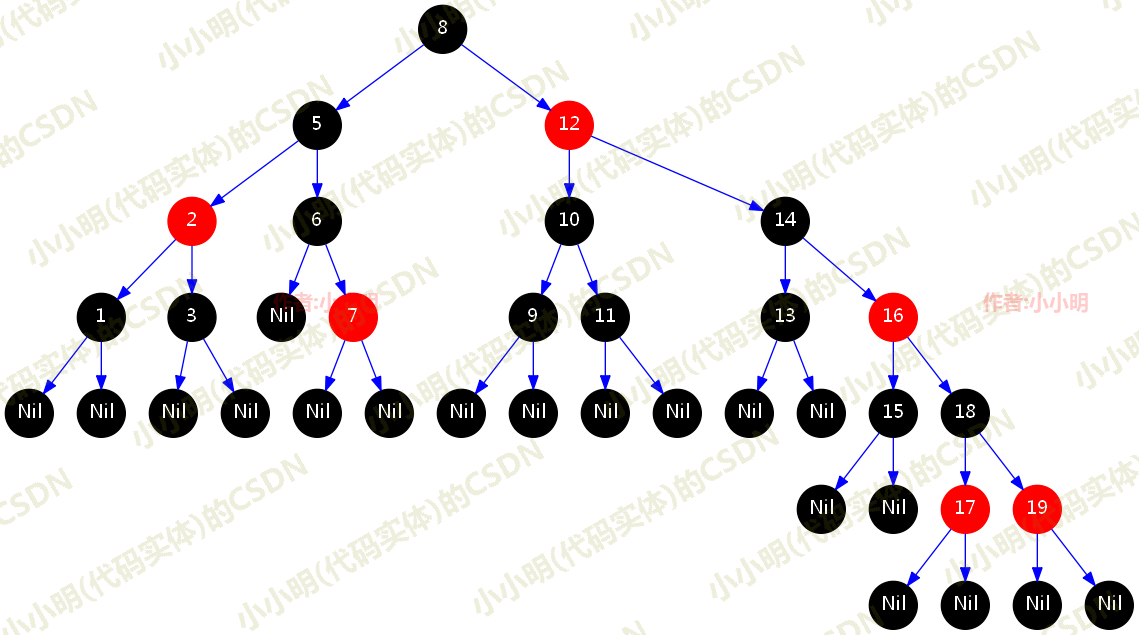
红黑树的英文是“Red-Black Tree”，简称 R-B Tree。它是一种不严格的平衡二叉查找树。顾名思义，红黑树中的节点，一类被标记为黑色，一类被标记为红色。除此之外，一棵红黑树还需要满足这样几个要求：

每个节点要么是红色，要么是黑色。
根节点必须是黑色，每个叶子节点是黑色（叶子节点包含NULL，也就是说，叶子节点不存储数据）。
- 为什么黑节点必须是黑色呢？根节点要么对应2-3树的2-节点或者3-节点，而这两者的根节点都是黑色的，因而根节点必然是黑色。
- 为什么叶子节点必须是黑色的空节点呢？这主要是为了简化红黑树的代码实现而设置的。
红色节点不能连续
- 红色节点的孩子和父亲都不能都是红色，即如果一个节点是红色的，则它的子节点必须是黑色的
- 也就是说任何相邻的节点都不能同时为空色，红色节点是被黑色节点隔开的。
- 由于红黑树的每个节点都由2-3树转换而来，红色节点连接的节点必然是一个2-节点或者3-节点，而无论是2-节点还是3-节点，其根节点都是黑色的，因此红色节点的子节点必然是黑色的
从任意节点出发，到其所有叶子节点的简单路径上都包含相同数目的黑色节点.

红黑树的发明过程

平衡二叉查找树

我们以这样一个数组为例 [42，37，18，12，11，6，5] 构建一棵二叉搜索树，由于数组中任意一点都可以作为二叉搜索树的根节点，因此这棵二叉搜索树并不唯一，我们来看一个极端的例子（以42作为根节点，顺序插入元素）

在这个例子中，二叉搜索树退化成了链表，搜索的时间复杂度为 O(n)，失去了作为一棵二叉搜索树的意义。

为了让二叉搜索树不至于太“倾斜”，我们需要构建一棵平衡二叉搜索树
在这里插入图片描述
可以看出，平衡二叉搜索树的搜索时间复杂度为O(logn)，避免了因为随机选取根节点构建二叉搜索树而可能造成的退化成链表的情况。下面再抄一段平衡二叉搜索树的官方定义：

平衡二叉查找树：简称平衡二叉树。是由前苏联的数学家 Adelse-Velskil和 Landis 在 1962 年提出的高度平衡的二叉树，根据科学家的英文名也称为 AVL 树。它具有如下几个性质：

可以是空树。
假如不是空树，任何一个结点的左子树与右子树都是平衡二叉树，并且高度之差的绝对值不超过 1

2-3树

经过上面的例子，我们可以知道，构建一颗平衡二叉搜索树的关键在于选取“正确”的根节点，那么我们如何在每次构建平衡二叉搜索树的时候都能选取合适的根节点呢？这里就要另一种重要的树：2-3树（读作二三树），2-3树和红黑树是等价的，理解2-3树对理解红黑树以及B类树都有很大的帮助。

为什么有了2-3树还需要有红黑树呢？

既然2-3树已经能够保持自平衡，为什么我们还需要一颗红黑树呢？

首先2-3树就是一个节点有1个或者2个元素，而实际上2-3树转红黑树是由概念模型2-3-4树转换而来的。4叉就是一个节点里有3个元素，这在2-3树中会被调整，但是在概念模型中是会被保留的。

虽然2-3-4树也是具备2-3树同样的平衡树的特性，但是如果直接把这样的模型用代码实现就会很麻烦，且效率不高，这里的复杂点包括；

2-叉、3-叉、4-叉，三种结构的节点类型，互相转换复杂度较高
3-叉、4-叉，节点在数据比较上需要进行多次，不像2-叉节点，直接布尔类型比较即可非左即右
代码实现上对每种差异，都需要有额外的代码，规则不够标准化

所以，希望找到一种平衡关系，既保持2-3树平衡和O(logn)的特性，又能在代码实现上更加方便，那么就诞生了红黑树。

也就是说：2-3树这种每个节点存储1-2个元素以及拆分节点向上融合的性质不便于代码操作。因此我们希望通过一些规则，将2-3树转换成二叉树，而且转换后的二叉树依然能够保持平衡。

红黑树实际上就是2-3树的二分搜索树表示，其中红节点于其父节点组合形成3节点，没有红色孩子节点的节点就是2节点
在这里插入图片描述

例如这颗红黑树中，这个红色的节点与其父节点（元素11所在的节点）组成一个3节点，这颗红黑树等价于以下的2-3树
在这里插入图片描述

总结：我们怎么将2-3树转换为红黑树

对于2节点，可以直接转换为红黑树中的一个黑节点
对于3节点：
- 将3节点拆开，成为一棵树，并且3节点的左元素作为又元素的子树
- 将原来的左元素标记为红色（表示红色节点于其父节点在2-3树种曾经是平衡关系）
  
  推论：由于红色节点是由3节点拆分而来，因此所有的红色节点只会出现在左子树上。

为什么说红黑树是“近似平衡”的

平衡二叉查找树的初衷，是为了解决二叉查找树因为动态更新导致的性能退化问题。所以，“平衡”的意思可以等价为性能不退化。“近似平衡”可以等价为性能不会退化的太严重

二叉查找树很多操作的性能都跟树的高度成正比。一棵极其平衡的二叉树（满二叉树或完全二叉树）的高度大约是 $log_2n$ ，所以如果要证明红黑树是近似平衡的，我们只需要分析，红黑树的高度是否比较稳定地趋近 $log_2n$ 就好了。

那怎么推导红黑树的高度呢？

（1）首先，我们来看，如果我们将红色节点从红黑树中去掉，那单纯包含黑色节点的红黑树的高度是多少呢？

红色节点删除之后，有些节点就没有父节点了，它们会直接拿这些节点的祖父节点（父节点的父节点）作为父节点。所以，之前的二叉树就变成了四叉树。

在这里插入图片描述

红黑树中的定义有这么一条：从任意节点到可达的叶子节点的每个路径包含相同数组的黑色节点。我们从四叉树中取出某些节点，放到叶节点位置，四叉树就变成了完全二叉树。所以，仅包含黑色节点的四叉树的高度，比包含相同个数的完全二叉树的高度还要小。
完全二叉树的高度近似 $log_2n$ ，这里的四叉“黑树”的高度要低于完全二叉树，所以去掉红色节点的“黑树”的高度也不会超过 $log_2n$ 。

（2）那我们现在把红色节点加回去，高度会变成多少呢？

在红黑树中，红色节点不能相邻，也就是说，有一个红色节点就要至少有一个黑色节点，将它跟其他红色节点隔开。
红黑树中包含最多黑色节点的路径不会超过 $log_2n$ ，所以加入红色节点之后，最长路径不会超过 $2log_2n$ ，也就是说，红黑树的高度近似 $2log_2n$

所以，红黑树的高度只比高度平衡的AVL树的高度 $log_2n$ 仅仅大了一倍，在性能上，下降的并不多。这样推导出来的结果不够精确，实际上红黑树的性能更好。

为什么工程中都用红黑树这种二叉树？

平衡二叉查找树其实有很多，比如，Splay Tree（伸展树）、Treap（树堆）等，但是我们提到平衡二叉查找树，听到的基本都是红黑树。它的出镜率甚至要高于“平衡二叉查找树”这几个字，有时候，我们甚至默认平衡二叉查找树就是红黑树，那为什么工程中都喜欢用红黑树，而不是其他平衡二叉查找树呢？

类似Treap、Splay Tree，绝大部分情况下，它们操作的效率都很高，但是也无法避免极端情况下时间复杂度的退化。尽管这种情况出现的概率不大，但是对于单次操作时间非常敏感的场景来说，它们并不适用
avl树是一种高度平衡的二叉树，所以查找的效率非常高。但是，有利就有弊，avl树为了维持这种高度的平衡，需要付出更多的代价。每次插入、删除都要做调整，就比较复杂、耗时。所以，对于有频繁的插入、删除操作的数据集合，使用avl树的代价就有些高了
红黑树只是做到了近似平衡，并不是严格的平衡，所以在维护平衡的成本上，要比avl树要低。

所以，红黑树的插入、删除、查找各种操作性能都比较稳定。对于工程应用来说，要面对各种异常情况，为了支撑这种工业级的应用，我们更倾向于这种性能稳定的平衡二叉查找树

小结我们学习数据结构和算法，要学习它的由来、特性、适用的场

红黑树它算是最难掌握的一种数据结构。不过呢，我认为，我们其实不应该把学习的侧重点，放到它的实现上。我们学习数据结构和算法，要学习它的由来、特性、适用的场景以及它能解决的问题。对于红黑树，也不例外。你如果能搞懂这几个问题，其实就已经足够了。

红黑树是一种平衡二叉查找树，它是为了解决普通二叉查找树在数据更新的过程中，复杂度退化的问题而产生的。红黑树的高度近似 $log_2n$ ，所以它是近似平衡，插入、删除、查找操作的时间复杂度都是O(logn)
因为红黑树是一种性能非常稳定的二叉查找树，所以，在工程中，但凡是用到动态插入、删除、查找数据的场景，都可以用到它。不过，它实现起来比较复杂，如果自己写代码实现，难度会有些高。这个时候，我们其实更倾向于用跳表替代它

所谓的动态数据结构是什么意思：

动态数据结构是支持动态的更新操作，里面存储的数据是时刻在变化的，通俗的一点讲，它不仅仅支持动态查询，还支持删除、插入数据。而且这些操作都非常高效。如果不高兴，也就是算不上有效的动态数据结构了
所以，这里的红黑树算一个，支持动态的插入、删除、查找，而且效率都很高。链表、队列、栈实际上算不上，因为操作非常有限，查询效率不高。
跳表，跳表也支持动态插入，删除，查询，也很快，不同点是跳表还能支持快速的范围查询。除此之外，跳表还支持多写多读，而红黑树不可以，这些场景下显然用跳表合适。