前段时间,小灰发布了红黑树相关的文章,分成上下篇来讲解。
这一次,小灰把两篇文章做了整合,并且修正了红黑树删除部分的图片错误,感谢大家的指正。
————— 第二天 —————
————————————
二叉查找树(BST)具备什么特性呢?
1.左子树上所有结点的值均小于或等于它的根结点的值。
2.右子树上所有结点的值均大于或等于它的根结点的值。
3.左、右子树也分别为二叉排序树。
下图中这棵树,就是一颗典型的二叉查找树:
1.查看根结点9:
2.根据二叉查找树左子树小、右子树大的特性,10 > 9,因此值为10的结点只可能在根结点的右子树当中,我们查看右孩子结点13:
3.由于10 < 13,因此查看左孩子11:
4.由于10 < 11,因此查看左孩子10,发现10正是要查找的结点:
假设初始的二叉查找树只有三个结点,根结点值为9,左孩子值为8,右孩子值为12:
接下来我们依次插入如下五个结点:7,6,5,4,3。依照二叉查找树的特性,结果会变成什么样呢?
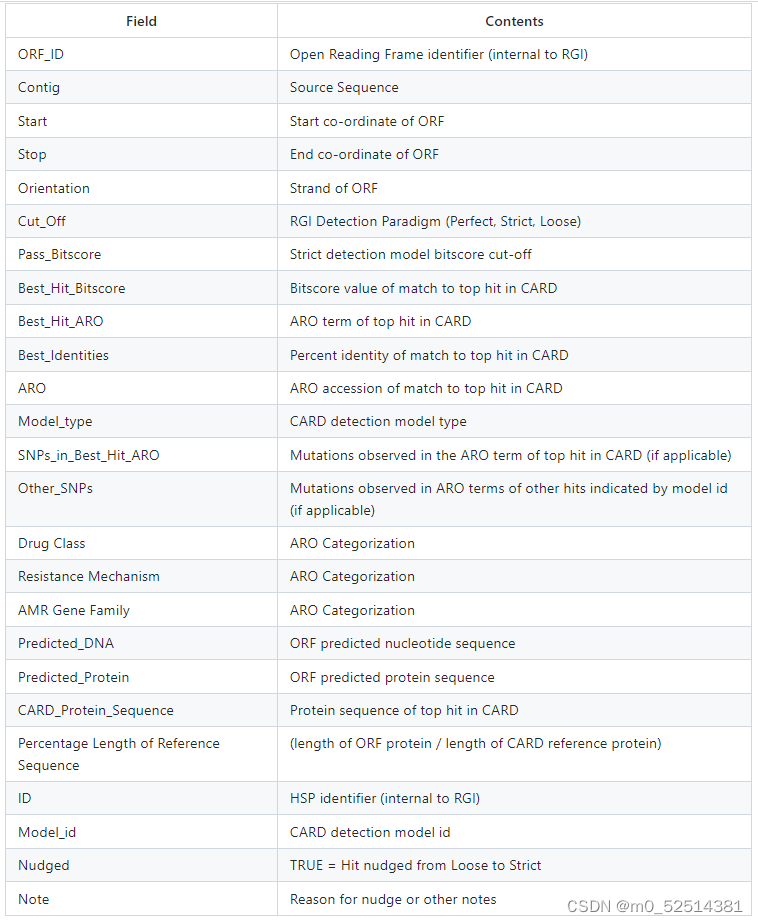
1.结点是红色或黑色。
2.根结点是黑色。
3.每个叶子结点都是黑色的空结点(NIL结点)。
4 每个红色结点的两个子结点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色结点)
5.从任一结点到其每个叶子的所有路径都包含相同数目的黑色结点。
下图中这棵树,就是一颗典型的红黑树:
什么情况下会破坏红黑树的规则,什么情况下不会破坏规则呢?我们举两个简单的例子:
1.向原红黑树插入值为14的新结点:
由于父结点15是黑色结点,因此这种情况并不会破坏红黑树的规则,无需做任何调整。
2.向原红黑树插入值为21的新结点:
由于父结点22是红色结点,因此这种情况打破了红黑树的规则4(每个红色结点的两个子结点都是黑色),必须进行调整,使之重新符合红黑树的规则。
变色:
为了重新符合红黑树的规则,尝试把红色结点变为黑色,或者把黑色结点变为红色。
下图所表示的是红黑树的一部分(子树),新插入的结点Y是红色结点,它的父亲结点X也是红色的,不符合规则4,因此我们可以把结点X从红色变成黑色:
但是,仅仅把一个结点变色,会导致相关路径凭空多出一个黑色结点,这样就打破了规则5。因此,我们需要对其他结点做进一步的调整,后文会详细说明。
左旋转:
逆时针旋转红黑树的两个结点,使得父结点被自己的右孩子取代,而自己成为自己的左孩子。说起来很怪异,大家看下图:
图中,身为右孩子的Y取代了X的位置,而X变成了自己的左孩子。此为左旋转。
右旋转:
顺时针旋转红黑树的两个结点,使得父结点被自己的左孩子取代,而自己成为自己的右孩子。大家看下图:
图中,身为左孩子的Y取代了X的位置,而X变成了自己的右孩子。此为右旋转。
局面1:新结点(A)位于树根,没有父结点。
(空心三角形代表结点下面的子树)
这种局面,直接让新结点变色为黑色,规则2得到满足。同时,黑色的根结点使得每条路径上的黑色结点数目都增加了1,所以并没有打破规则5。
局面2:新结点(B)的父结点是黑色。
这种局面,新插入的红色结点B并没有打破红黑树的规则,所以不需要做任何调整。
局面3:新结点(D)的父结点和叔叔结点都是红色。
这种局面,两个红色结点B和D连续,违反了规则4。因此我们先让结点B变为黑色:
这样一来,结点B所在路径凭空多了一个黑色结点,打破了规则5。因此我们让结点A变为红色:
这时候,结点A和C又成为了连续的红色结点,我们再让结点C变为黑色:
经过上面的调整,这一局部重新符合了红黑树的规则。
局面4:新结点(D)的父结点是红色,叔叔结点是黑色或者没有叔叔,且新结点是父结点的右孩子,父结点(B)是祖父结点的左孩子。
我们以结点B为轴,做一次左旋转,使得新结点D成为父结点,原来的父结点B成为D的左孩子:
这样一来,进入了局面5。
局面5:新结点(D)的父结点是红色,叔叔结点是黑色或者没有叔叔,且新结点是父结点的左孩子,父结点(B)是祖父结点的左孩子。
我们以结点A为轴,做一次右旋转,使得结点B成为祖父结点,结点A成为结点B的右孩子:
接下来,我们让结点B变为黑色,结点A变为红色:
经过上面的调整,这一局部重新符合了红黑树的规则。
以上就是红黑树插入操作所涉及的5种局面。
或许有人会问,如果局面4和局面5当中的父结点B是祖父结点A的右孩子该怎么办呢?
很简单,如果局面4中的父结点B是右孩子,则成为了局面5的镜像,原本的右旋操作改为左旋;如果局面5中的父结点B是右孩子,则成为了局面4的镜像,原本的左旋操作改为右旋。
给定下面这颗红黑树,新插入的结点是21:
显然,新结点21和它的父结点22是连续的红色结点,违背了规则4,我们应该如何调整呢?
让我们回顾一下刚才讲的5种局面,当前的情况符合局面3:
“新结点的父结点和叔叔结点都是红色。”
于是我们经过三次变色,22变为黑色,25变为红色,27变为黑色:
经过上面的调整,以结点25为根的子树符合了红黑树规则,但结点25和结点17成为了连续的红色结点,违背规则4。
于是,我们把结点25看做一个新结点,正好符合局面5的镜像:
“新结点的父结点是红色,叔叔结点是黑色或者没有叔叔,且新结点是父结点的右孩子,父结点是祖父结点的右孩子”
于是我们以根结点13为轴进行左旋转,使得结点17成为了新的根结点:
接下来,让结点17变为黑色,结点13变为红色:
如此一来,我们的红黑树变得重新符合规则。
二叉查找树是如何进行删除操作的呢?可以分成三种情况。
情况1,待删除的结点没有子结点:
上图中,待删除的结点12是叶子结点,没有孩子,因此直接删除即可:
情况2,待删除的结点有一个孩子:
上图中,待删除的结点13只有左孩子,于是我们让左孩子结点11取代被删除的结点,结点11以下的结点关系无需变动:
情况3,待删除的结点有两个孩子:
上图中,待删除的结点5有两个孩子,这种情况比较复杂。此时,我们需要选择与待删除结点最接近的结点来取代它。
上面的例子中,结点3仅小于结点5,结点6仅大于结点5,两者都是合适的选择。但习惯上我们选择仅大于待删除结点的结点,也就是结点6来取代它。
于是我们复制结点6到原来结点5的位置:
被选中的结点6,仅大于结点5,因此一定没有左孩子。所以我们按照情况1或情况2的方式,删除多余的结点6:
红黑树的特性(规则)如下:
1.结点是红色或黑色。
2.根结点是黑色。
3.每个叶子结点都是黑色的空结点(NIL结点)。
4.每个红色结点的两个子结点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色结点)
5.从任一结点到其每个叶子的所有路径都包含相同数目的黑色结点。
下面我们通过一个例子,来看一看删除红黑树的结点会对规则产生怎样的影响:
上图的这颗红黑树,待删除的是黑色结点1,有一个右孩子。根据二叉查找树的删除流程,我们让右孩子结点6直接取代结点1:
显然,这颗新的二叉树打破了两个规则:
规则4. 每个红色结点的两个子结点都是黑色。
规则5. 从任一结点到其每个叶子的所有路径都包含相同数目的黑色结点。
第一步:如果待删除结点有两个非空的孩子结点,转化成待删除结点只有一个孩子(或没有孩子)的情况。
上面例子是一颗红黑树的局部,标数字的三角形代表任意形态的子树,假设结点8是待删除结点。
根据上文讲解的二叉查找树删除流程,由于结点8有两个孩子,我们选择仅大于8的结点10复制到8的位置,结点颜色变成待删除结点的颜色:
接下来我们需要删除红色的结点10:
红色结点10能成为仅大于8的结点,必定没有左孩子结点,所以问题转换成了待删除结点只有一个右孩子(或没有孩子)的情况。接下来我们进入第二步。
第二步:根据待删除结点和其唯一子结点的颜色,分情况处理。
情况1,自身是红色,子结点是黑色:
这种情况最简单,按照二叉查找树的删除操作,删除结点1即可:
情况2,自身是黑色,子结点是红色:
这种情况也很简单,首先按照二叉查找树的删除操作,删除结点1:
此时,这条路径凭空减少了一个黑色结点,那么我们把结点2变成黑色即可:
情况3,自身是黑色,子结点也是黑色,或者子结点是空叶子结点:
这种情况最复杂,涉及到很多变化。首先我们还是按照二叉查找树的删除操作,删除结点1:
显然,这条路径上减少了一个黑色结点,而且结点2再怎么变色也解决不了。
这时候我们进入第三步,专门解决父子双黑的情况。
第三步:遇到双黑结点,在子结点顶替父结点之后,分成6种子情况处理。
子情况1,结点2是红黑树的根结点:
此时所有路径都减少了一个黑色结点,并未打破规则,不需要调整。
子情况2,结点2的父亲、兄弟、侄子结点都是黑色:
此时,我们直接把结点2的兄弟结点B改为红色:
这样一来,原本结点2所在的路径少了一个黑色结点,现在结点B所在的路径也少了一个黑色结点,两边“扯平”了。
可是,结点A以下的每一条路径都减少了一个黑色结点,与结点A之外的其他路径又造成了新的不平衡啊?
没关系,我们让结点A扮演原先结点2的角色,进行递归操作,重新判断各种情况。
子情况3,结点2的兄弟结点是红色:
首先以结点2的父结点A为轴,进行左旋:
然后结点A变成红色、结点B变成黑色:
这样的意义是什么呢?结点2所在的路径仍然少一个黑色结点呀?
别急,这样的变化有可能转换成子情况4、5、6中的任意一种,在子情况4、5、6当中会进一步解决。
子情况4,结点2的父结点是红色,兄弟和侄子结点是黑色:
这种情况,我们直接让结点2的父结点A变成黑色,兄弟结点B变成红色:
这样一来,结点2的路径补充了黑色结点,而结点B的路径并没有减少黑色结点,重新符合了红黑树的规则。
子情况5,结点2的父结点随意,兄弟结点B是黑色右孩子,左侄子结点是红色,右侄子结点是黑色:
这种情况下,首先以结点2的兄弟结点B为轴进行右旋:
接下来结点B变为红色,结点C变为黑色:
这样的变化转换成了子情况6。
子情况6,结点2的父结点随意,兄弟结点B是黑色右孩子,右侄子结点是红色:
首先以结点2的父结点A为轴左旋:
接下来让结点A和结点B的颜色交换,并且结点D变为黑色:
这样是否解决了问题呢?
经过结点2的路径由(随意+黑)变成了(随意+黑+黑),补充了一个黑色结点;
经过结点D的路径由(随意+黑+红)变成了(随意+黑),黑色结点并没有减少。
所以,这时候重新符合了红黑树的规则。
以上就是红黑树删除的全过程。
给定下面这颗红黑树,待删除的是结点17:
第一步,由于结点17有两个孩子,子树当中仅大于17的结点是25,所以把结点25复制到17位置,保持黑色:
接下来,我们需要删除原本的结点25:
这个情况正好对应于第二步的情况三,即待删除结点是黑色,子结点是空叶子结点。
于是我们删除框框中结点25,进入第三步:
此时,框框中的结点虽然是空叶子结点,但仍然可以用于判断局面,当前局面符合子情况5的镜像:
于是我们通过左旋和变色,把子树转换成情况6的镜像:
再经过右旋、变色,子树最终成为了下面的样子:
这样一来,整颗二叉树又重新符合了红黑树的规则。
推荐阅读:
小灰 “生二胎” 啦!
喜欢本文的朋友,欢迎关注公众号 程序员小灰,收看更多精彩内容
点个[在看],是对小灰最大的支持!