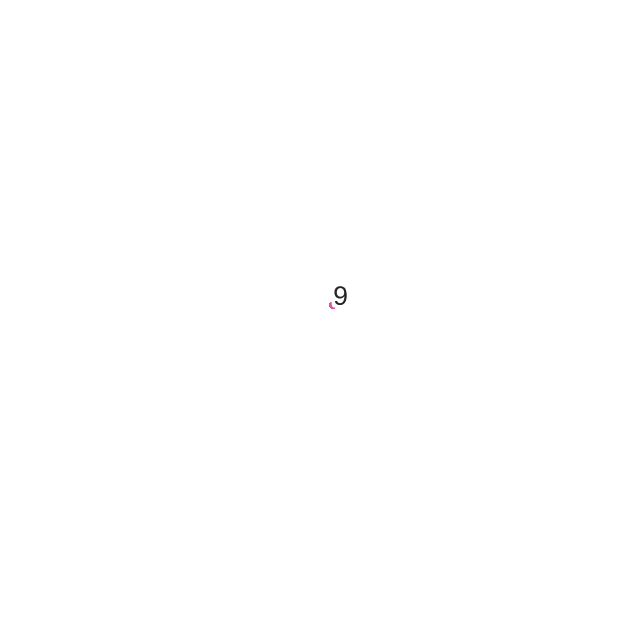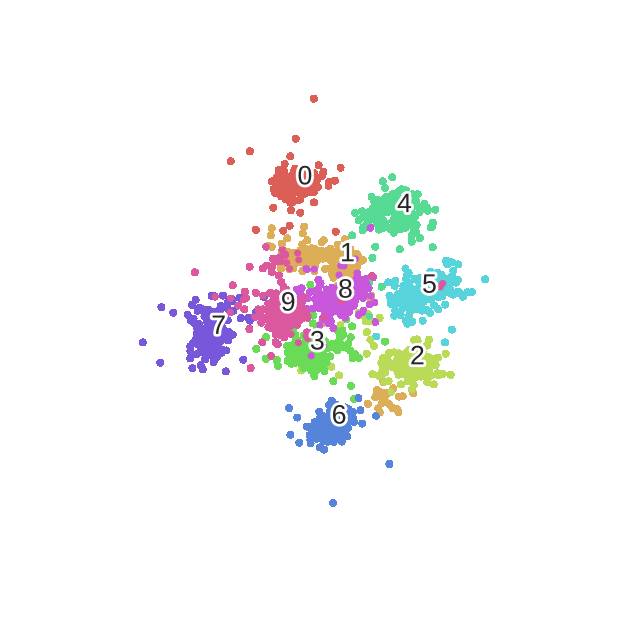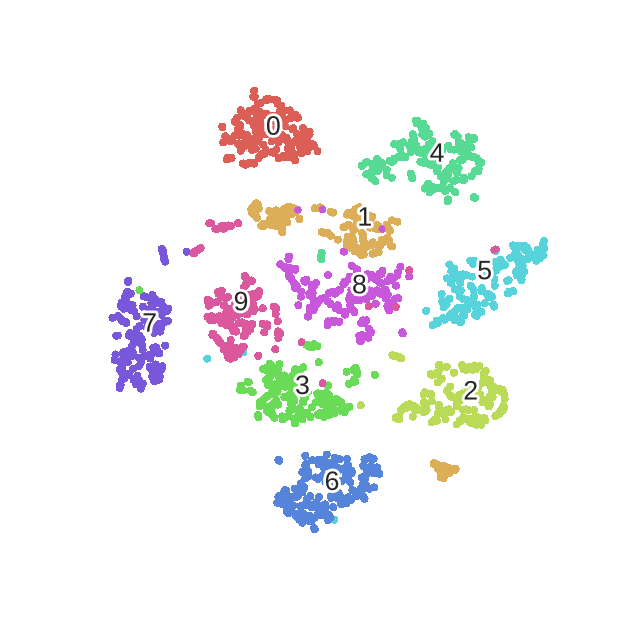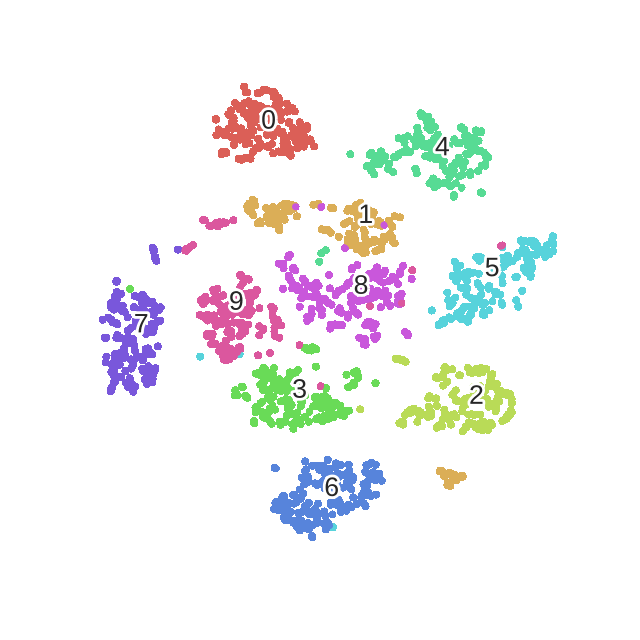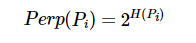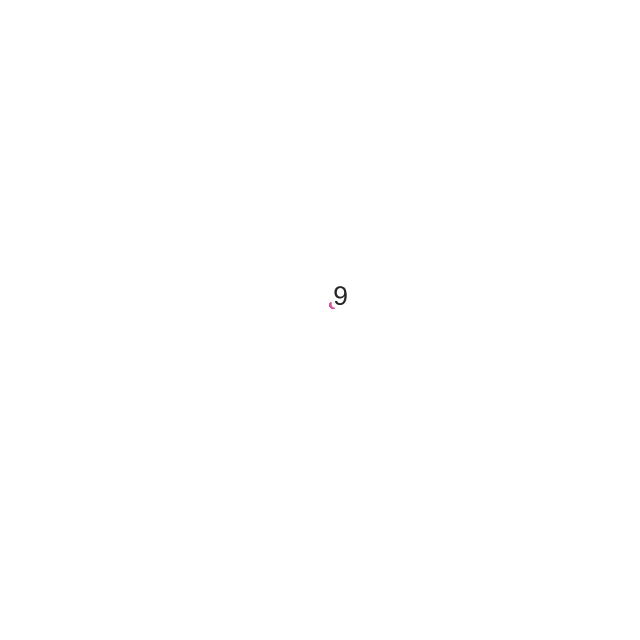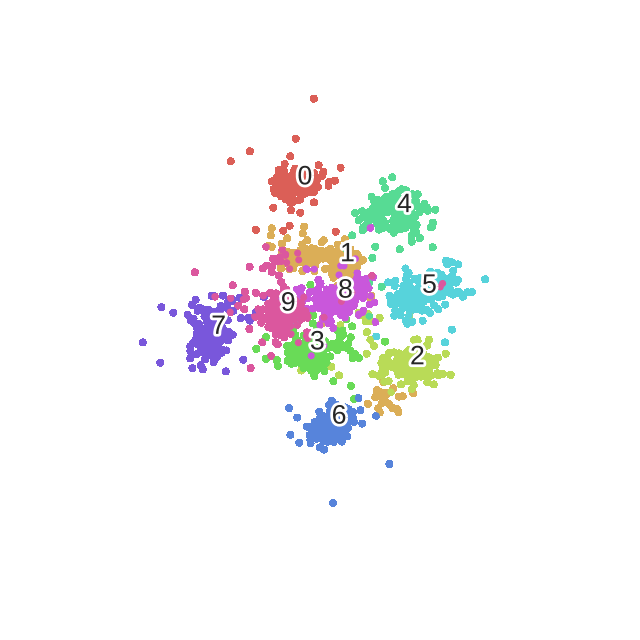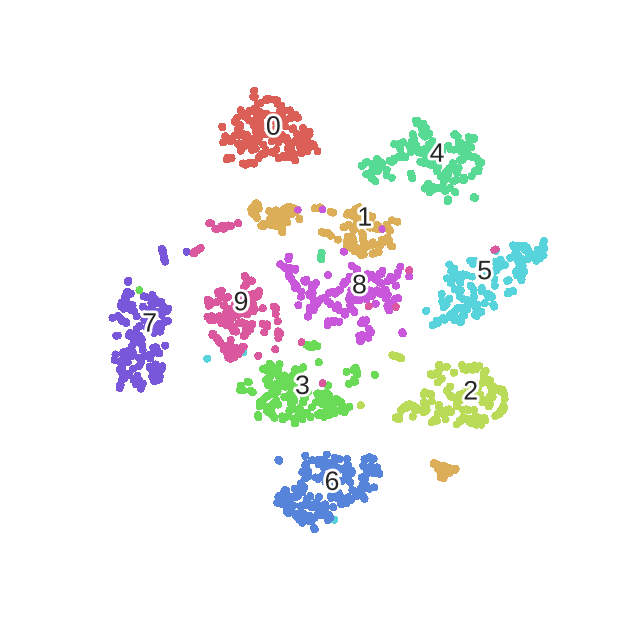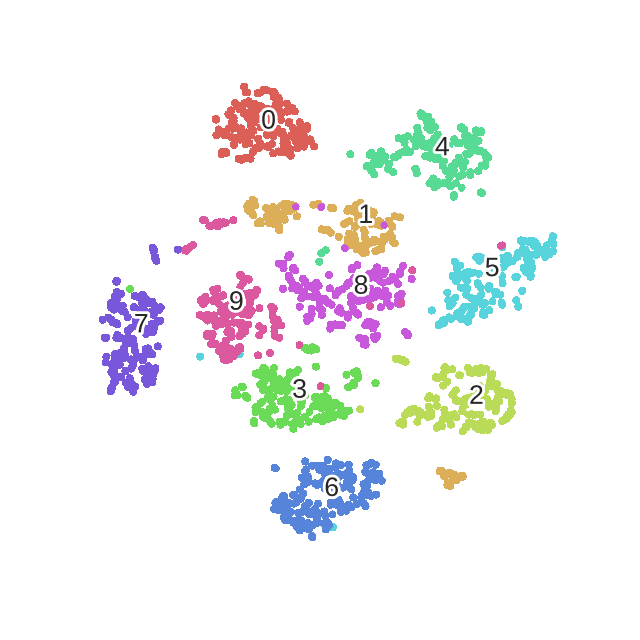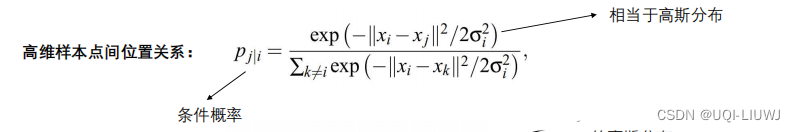t-SNE数据降维可视化 – 潘登同学的Machine Learning笔记

是最近遇到了bertopic中，使用的UMAP降维ie方法，说是能吊打t-SNE，但之前我做Word2Vec的时候也是用的t-SNE，所以学习一下，并且做一下两者的对比

t-SNE的基本思想

t-SNE是一种非常常用的数据降维(数据可视化)，基本思想是

1. 在高维空间构建一个概率分布拟合高维样本点间的相对位置
2. 在低维空间，也构建一个概率分布拟合高维样本点之间的位置关系
3. 通过学习，调整低维数据点，令两个分布接近

SNE(Stochastic Neighbor Embedding)

SNE直译过来是随机邻域嵌入；

为了衡量高维数据的相似性,用条件概率表示高维样本点间的位置关系：
$$p_{j|i}=\frac{e^{-\frac{||x_i-x_j|{|}^2}{2{\sigma }_i^2}}}{{\sum }_{k\ne i}{e}^{-\frac{||x_i-x_k|{|}^2}{2{\sigma }_i^2}}}$$
当然地，当点$i$与点$j$的距离越近，$p_{j|i}$就越大；

我们要考虑映射后的低维空间的数据分布，同样可以用条件概率来表示:
$$q_{j|i}=\frac{e^{-||y_i-y_j|{|}^2}}{{\sum }_{k\ne i}{e}^{-||y_i-y_k|{|}^2}}$$

为了让两个分布更相近，采用KL散度对其进行衡量
$$C=\sum _{i}KL(P_i||Q_i)=\sum _i\sum _j{p}_{j|i}\log \frac{p_{j|i}}{q_{j|i}}$$
调整$y$最小化C，实现降维

SNE的主要缺点

距离不对称

根据上面的公式会得到$p_{j|i}\ne p_{i|j}$,改进方法
$$\begin{gathered} p_{ij}=\frac{e^{-\frac{||x_i-x_j|{|}^2}{2{\sigma }_i^2}}}{{\sum }_{k\ne l}{e}^{-\frac{||x_l-x_k|{|}^2}{2{\sigma }_i^2}}} \\ {q}_{ij}=\frac{e^{-||y_i-y_j|{|}^2}}{{\sum }_{k\ne l}{e}^{-||y_l-y_k|{|}^2}} \end{gathered}$$
简单来说就是把分母变成所有点两两距离之和；

但是会有更好的方法保证对称：
$$\begin{gathered} p_{ij}=p_{i|j}+p_{j|i}\text{(保证对称)} \\ {p}_{ij}=\frac{p_{ij}}{{\sum }_i{\sum }_j{p}_{ij}}\text{(保证归一化)} \end{gathered}$$

存在拥挤现象

从高维到低维进行转换的过程中，低维点的距离无法建模高维点之间的位置关系，有可能高维空间中距离较大的点，在低维空间距离会变得较小；

换言之，哪怕高维空间中离得较远的点，在低维空间中留不出这么多空间来映射。于是到最后高维空间中的点，尤其是远距离和中等距离的点，在低维空间中统统被塞在了一起，这就叫做“拥挤问题（Crowding Problem）

高维空间保持高斯分布不变，将低维空间的分布做调整，使得两边尾巴比高维空间的高斯分布更高，即可缓解拥挤问题；

$$q_{ij}=\frac{(1+||y_i-y_j|{|}^2{)}^{-1}}{{\sum }_{k\ne l}(1+||y_k-y_l|{|}^2{)}^{-1}}$$

假设我们的低维数据分布对高维数据分布已经拟合完毕，则可以认为对于高维数据点$x_i、x_j$和低维映射点$y_i、y_j$，有$p_{ij}=q_{ij}$。我们用图中两条红线表示两种情况：

1. 上面的红线表示：当两个点相距相对近的时候，低维空间中比高维空间中相对更近。
2. 下面的红线表示：当两个点相距相对远的时候，低维空间中比高维空间中相对更远。

如何确定$\sigma$

设置一个固定的参数： Perplexity表示分布的熵，设法调节每个${\sigma }_i$,使得
$$\log (Per)=-\sum _j{p}_{j|i}\log (p_{j|i})$$
根据$p_{j|i}$的计算公式，距离$x_i$小于$2\sigma$的点对p的计算起主要作用，故

• 当$x_i$临近点较多的时候： 减少$\sigma$
• 当$x_i$临近点较多=少的时候： 增大$\sigma$

总结t-sne

1. 计算$p_{j|i}$,利用结果，计算$p_{ij}$
   $$p_{j|i}=\frac{e^{-\frac{||x_i-x_j|{|}^2}{2{\sigma }_i^2}}}{{\sum }_{k\ne i}{e}^{-\frac{||x_i-x_k|{|}^2}{2{\sigma }_i^2}}}$$
   $$p_{ij}=p_{i|j}+p_{j|i},p_{ij}=\frac{p_{ij}}{{\sum }_i{\sum }_j{p}_{ij}}$$
2. 随机生成低维随机数并计算：
   $$q_{ij}=\frac{(1+||y_i-y_j|{|}^2{)}^{-1}}{{\sum }_{k\ne l}(1+||y_k-y_l|{|}^2{)}^{-1}}$$
3. 利用梯度下降法令C最小
   $$C=KL(P||Q)=\sum _i\sum _j{p}_{ij}\log p_{ij}{q}_{ij}$$

代码实现

对mnist手写数据集做t-sne数据降维

初始化结果

第100次迭代

算法收敛

对比t-sne与UMAP

t-sne有以下缺点

• tSNE实际上只能嵌入到2维或3维中，即只能用于可视化的目的，所以很难将tSNE作为一般的降维技术；
• tSNE不能直接处理高维数据，通常使用Autoencoder或PCA进行降维处理，然后将降维的结果输入tsne做可视化。

t-sne与UMAP的对比

• UMAP是一种新颖且有趣的降维技术，与纯机器学习半经验算法tSNE截然不同，它基于可靠的数学原理。
• UMAP使用高维度上的指数概率分布，但不一定要像tSNE那样使用欧几里得距离，而是可以插入任何距离。
• UMAP在计算$p_{j|i}$的时候只考虑K个近邻点的距离，而且无需归一化，极大减少计算量； 除此之外 ， 在计算距离的时候减去了一个${\rho }_i$,确保了流型的连通性；
• UMAP在低维的概率表示也是使用欧式距离，但是不再使用t分布，转而使用一个曲线拟合的方式（但是与t分布比较相似),再次提到，这里也不用归一化；
• UMAP的Loss函数采用的是交叉熵，无论高维数据距离很大还是很小，都很容易调整低维数据(因为Loss函数的梯度在极端处很大(UMAP处说到过))
• 与tSNE使用的随机法线初始化相反，UMAP使用Graph Laplacian分配初始低维坐标。(但是对结果影响不大，可能能减少计算量)