1.原图片

小灰灰图片

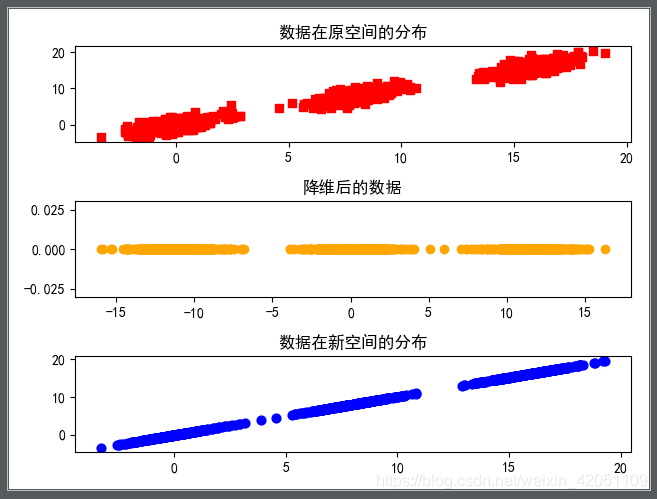
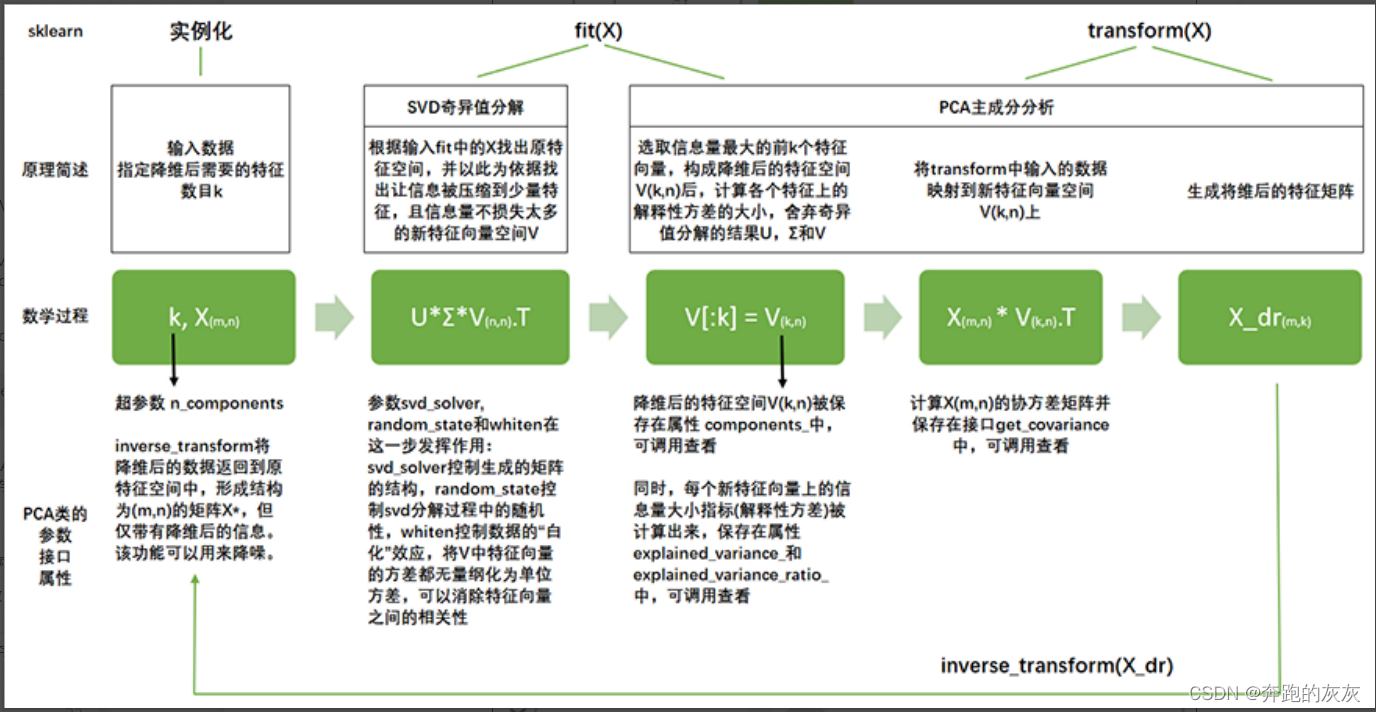
2.PCA降维思路

    1、小灰灰图片（407，367）2、求图片407行每行的均值mean，再将407行每行元素各自减去对应行的均值mean，即去中心化。得矩阵X（407，367）3、为求特征，需要矩阵X为方阵，故方阵C＝X^T * X。的矩阵C（367，367）4、求C的特征值（367，1）和特征向量（367，367）5、取前k个最大特征值对应的特征向量。得k个特征向量Vec，也就是k个基（367，k）6、将去中心化了的原图片矩阵X在这k个基中投影，在基中降维为k的新矩阵D=X ＊ Vec。得D（407，k）［注］因为Vec矩阵（367，k）中k的不同取值，会导致原图丢失信息，故恢复后的图片与原图片不同另外，当k＝367时，将不会丢失信息，k值越少，丢失信息越多，因为降维只取了k个最主要的成分7、将降维后的矩阵恢复为图片：X'＝D ＊ Vec^T。得X'（407，367）［注］因此降维后图片与原图尺寸相同

3.代码

from PIL import Imageimport numpy as np
import os"""参数说明：file_path：该路径存放原图片和产生的灰度图片work_path：该路径存放pca处理后的图片，图片编号代表此图片使用了多少特征数img_path：用于判断，不必理会
"""
file_path = './img/'
work_path = './pcaImg/'
img_path = file_path + '1.jpg'#用于创建文件夹，不必理会
if not os.path.exists(file_path):os.mkdir(file_path)
if not os.path.exists(img_path):print('请在img文件夹中添加一张照片并将其命名为1.jpg')exit()
if not os.path.exists(work_path):os.mkdir(work_path)"""函数功能：将原图片变为灰度图片参数说明：path：原图片路径输出说明：data：灰度图片像素数组
"""
def loadImage(path):# 打开图片img = Image.open(path)# 将图像转换成灰度图img = img.convert("L")# 图像对象，可变为数组data = img.getdata()# size中1为长，0为宽# 为了避免溢出，这里对数据进行一个缩放，缩小100倍data = np.array(data).reshape(img.size[1], img.size[0])/100# 查看原图的话，需要还原数据new_im = Image.fromarray(data*100)# 将图片保存在路径中# 一定要写convert()不然会一直报错cannot write mode F as JPEG或者keyerrornew_im.convert('RGB').save(file_path+'gImg.jpg', format='jpeg')# 展示灰度图片# new_im.show()return data"""函数功能：使用pca对灰度图片进行降维处理参数说明：data：灰度图路径k：主成分个数输出说明：pass
"""
def pca(data, k):# 求图片每一行的均值mean = np.array([np.mean(data[:, index]) for index in range(data.shape[1])])# 去中心化normal_data = data - mean# 得到协方差矩阵：1/n＊(X * X^T)，这里不除以n也不影响matrix = np.dot(np.transpose(normal_data), normal_data)# 此函数可用来计算特征值及对应的特征向量# eig_val存储特征值，eig_vec存储对应的特征向量eig_val, eig_vec = np.linalg.eig(matrix)# 对矩阵操作，按从小到大的顺序对应获得此数的次序（从0开始）# 比如说有矩阵[2,1,3,－1]# 那么将按数组的顺序[－1,1，2，3］输出对应的下标# 即[2，1，3，0]eig_index = np.argsort(eig_val)# 取下标的倒数k位，也就是取前k个大特征值的下标eig_vec_index = eig_index[:-(k+1):-1]# 取前k个大特征值的特征向量feature = eig_vec[:, eig_vec_index]# 将特征值与对应特征向量矩阵乘得到最后的pca降维图new_data = np.dot(normal_data, feature)# 将降维后的数据映射回原空间rec_data = np.dot(new_data, np.transpose(feature)) + mean# 压缩后的数据也需要乘100还原成RGB值的范围newImage = Image.fromarray(np.uint8(rec_data*100))# 将处理好的降维图片存入文件夹newImage.convert('RGB').save(work_path + 'k=' + str(k) + '.jpg')# newImage.show()if __name__ == '__main__':data = loadImage(img_path)for i in range(1, data.shape[1]+1):pca(data, i)print('正在处理第', str(i) + '/' + str(data.shape[1]), '张图片')print('处理完成，请查看pcaImg文件夹')