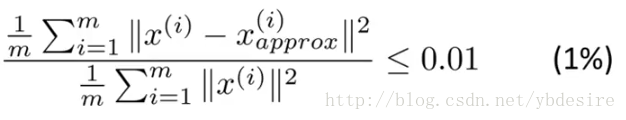python实现PCA降维

article/2025/10/13 19:35:20

本文包括两部分，使用python实现PCA代码及使用sklearn库实现PCA降维，不涉及原理。

总的来说，对n维的数据进行PCA降维达到k维就是：

  1. 对原始数据减均值进行归一化处理；
  2. 求协方差矩阵；
  3. 求协方差矩阵的特征值和对应的特征向量；
  4. 选取特征值最大的k个值对应的特征向量；
  5. 经过预处理后的数据乘以选择的特征向量，获得降维结果。

 

实验数据

数据data.txt使用[2]中编写的数据，以下是部分数据截图：

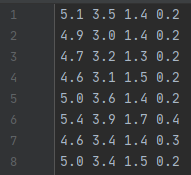
shape为(31, 4)，即31条特征数为4的数据。

 

使用python实现PCA

完整代码参考[2]，这里逐步做详细介绍。

1. 导入数据

import numpy as np
import pandas as pddatafile = "data.txt"
XMat = np.array(pd.read_csv(datafile,sep=" ",header=None)).astype(np.float)
XMat.shape
(31, 4)

2. 去除平均值

求得XMat每列的平均值：

average = np.mean(XMat, axis=0)
average
array([5.01935484, 3.43870968, 1.47741935, 0.24516129])

扩展均值shape由(1, 4)到(31, 4)： 

# avgs为average的前m=31行，因为average只有1行，因此这31行是一样的
# np.tile(average, (m, 1))表示是二维的,m行4列
m, n = np.shape(XMat)
avgs = np.tile(average, (m, 1))
print(avgs.shape)# np.tile(average, m)是一维的，有m*4个值
print(np.tile(average, m))
print(np.tile(average, m).shape)
(31, 4)
avgs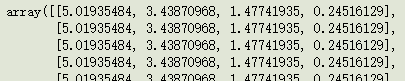

 XMat减去其每列均值：

data_adjust = XMat - avgs
data_adjust

3. 求XMat协方差矩阵的特征值和特征向量

因为是4列的数据即4维特征，因此协方差是4x4的：

covX = np.cov(data_adjust.T)
covX
array([[0.1356129 , 0.10022581, 0.01645161, 0.01576344],[0.10022581, 0.12245161, 0.00023656, 0.01919355],[0.01645161, 0.00023656, 0.03380645, 0.0053871 ],[0.01576344, 0.01919355, 0.0053871 , 0.00989247]])

特征值 0.23301081 对应特征向量为第一条列向量 [-0.72506043,-0.67669491,-0.06368499,-0.11097564]，这里的特征向量都归一化为单位向量：

featValue, featVec=  np.linalg.eig(covX)
featValue
featVec
array([0.23301081, 0.04211748, 0.02128637, 0.00534878])array([[-0.72506043, -0.39050501,  0.5585571 ,  0.09903116],[-0.67669491,  0.49557031, -0.48975083, -0.23798779],[-0.06368499, -0.77541379, -0.58351247, -0.23278934],[-0.11097564, -0.02548266, -0.32813302,  0.93774397]])

4. 选择最大的k个特征值对应的k个特征向量

按照特征值从大到小排序,index显示位置： 

index = np.argsort(-featValue)
index# 下面是从小到大
np.argsort(featValue)
array([0, 1, 2, 3], dtype=int64)array([3, 2, 1, 0], dtype=int64)

因为特征向量是列向量，这里转化成横向量： 

k = 2
selectVec = np.matrix(featVec.T[index[:k]])
selectVec
matrix([[-0.72506043, -0.67669491, -0.06368499, -0.11097564],[-0.39050501,  0.49557031, -0.77541379, -0.02548266]])

5. 将样本点投影到选取的特征向量上

即数据集*特征向量的转置：

finalData = data_adjust * selectVec.T # (31, 4) * (4, 2) = (31, 2)
finalData.shape
finalData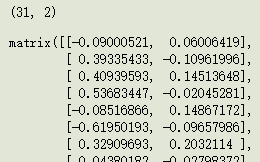

6. 计算重构误差[3]

还原对应投影后的数据：

reconData = (finalData * selectVec) + average
print(reconData.shape)
reconData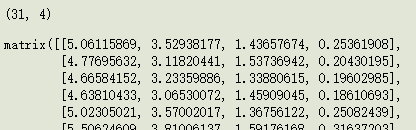

根据[4]中的：

这里写图片描述

其中，m是样本个数，即数据的行数31。x是经过去均值处理的原始数据，这里是data_adjust。x(approx)是经过重构后还原的数据，这里是reconData。

求误差平方和，计算err1：

errMat = XMat - reconData
err1 = np.sum(np.array(errMat)**2) / n
err1
0.19976362846119633

计算err2：

err2 = np.sum(data_adjust**2) / n
err2
2.2632258064516138

计算η：

eta = err1/err2
eta
0.0882650011729915

根据[4]，1-η=91%左右，说明该数据取k=2进行PCA降维时，能保留91%以上的信息。

 

使用sklearn库实现PCA降维

PCA的api详见[5]，下面说明一些常用的属性和方法。

from sklearn.decomposition import PCApca = PCA(n_components=k)
pca.fit(XMat)

1. n_components参数：

  • 默认值为保留所有特征值，即不进行降维：
pca = PCA()
pca.fit(XMat)
pca.explained_variance_
array([0.23301081, 0.04211748, 0.02128637, 0.00534878])

explained_variance_ 即协方差矩阵的k个最大特征值，这里n_components是默认值，因此k=4。

  • n_components == 'mle' 时， 会自动确认降维维度，但是好像结果就是n-1（n是原始数据的列数，即特征个数）：
pca.explained_variance_
array([0.23301081, 0.04211748, 0.02128637])

k=3的结果。

  • 0 < n_components < 1 时，即指定降维后的 方差和 占比，比例越大，降维后保留的信息越多，会自动确认降维的维度。

当n_components=0.9时是k=2的效果，n_components=0.95时是k=3的效果。

可以通过[6]中的画图来获取想要保留的信息和维度的关系：

import matplotlib.pyplot as pltdef pcaImg(XMat):pca=PCA( )pca.fit(XMat)ratio=pca.explained_variance_ratio_k = pca.n_components_print("pca.n_components_", k)# 绘制图形x = [i+1 for i in range(k)]y = [np.sum(ratio[:i+1]) for i in range(k)]print(y)plt.plot(x, y)plt.xticks(1+np.arange(k,step=1))plt.yticks(np.arange(0,1.01,0.05))plt.grid()plt.show()pcaImg(XMat)

 

横坐标表示k，纵坐标表示降维后可保留的信息。

可以看到，当k=1时能保留大概77%的信息；k=2时为91%，k=3时为98%，k=4时即没有降维，没有损失信息。

取 n_components = 0.9 时，打印结果：

确实是k=2。

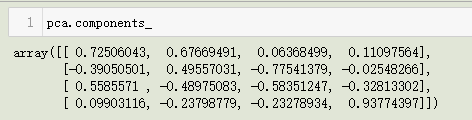
2. components_ 属性

输出k个特征向量，每一行代表一个特征向量：

3. explained_variance_ 属性

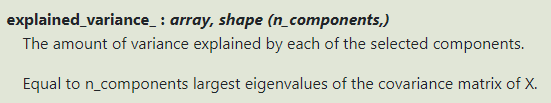
输出所选择的k个最大特征值：

4. explained_variance_ratio_ 属性

保留的维度的方差百分比，就是每个特征值占其所有特征值总值的占比：

即k=1时，降维后可保留的信息为77%，k=2时为77%+24%等。

一般来说，占比过小的可以舍弃，即这里取k=2或3较好，具体情况具体分析。

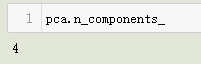
5. n_components_ 属性

即设置的降维维度k：

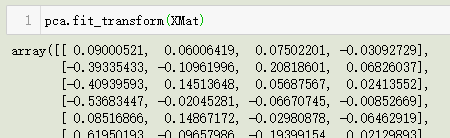
6. fit_transform(X[, y]) 方法

获得降维后的结果，和 transform(X) 方法差不多：

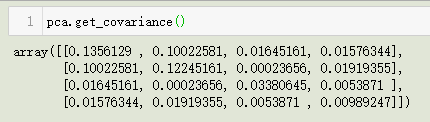
7. get_covariance() 方法

获得协方差矩阵：

8. inverse_transform(X) 方法

由降维结果返回原始结果：

这里因为k=n，所有还原后就是原始值，实际上当k<n时就跟上面一样是有误差的。

 

总结

当数据维度过高时可使用降维手段如PCA，来使得维度变低，避免维度灾难，同时加快运算速度。

PCA降维本质上就是一种信息压缩，如把shape为(31, 4)的数据压缩为(31, 2)。

关于降维维度k的确定，可以使用sklearn中的PCA模块来获取数据的方差百分比，根据以上绘图的方法来确定最佳k值。

有些研究工作表明，所选的主轴总长度占所有主轴长度之和的大约85% 即可。即保留的维度的方差总百分比到达85%以上，但实际效果还是依靠训练之后产生的预测结果的评估来决定。

确定好了k值后，即可快速根据API获取降维后的数据，来进行后续的实验。

 

参考文档

[1] 降维算法一 : PCA (Principal Component Analysis)

[2] 机器学习降维之PCA（python代码+数据）

[3] PCA降维以及维数的确定

[4] PCA主成分数量（降维维度）选择

[5] sklearn.decomposition.PCA

[6] 通过PCA选择合适降维维度


http://chatgpt.dhexx.cn/article/MnB1y2Tq.shtml

相关文章

PCA算法

PCA算法

主成分分析&#xff08;Principal components analysis&#xff0c;以下简称PCA&#xff09;是最重要的降维方法之一。 参考&#xff1a;http://www.cnblogs.com/pinard/p/6239403.html PCA的思想 PCA顾名思义&#xff0c;就是找出数据里最主要的方面&#xff0c;用数据里最…
阅读更多...
PCA

PCA

R语言实现PCA 一次来自男神MR.来的作业PCA读取数据PCA主体部分输出PCA的主要结果&#xff0c;列出主成分分析分析结果利用碎石图来展示PCA结果对component进行一些解释 简略分析利用PCA结果来进行一个排序下面进行聚类分析 一次来自男神MR.来的作业 PCA 读取数据 #读取数据&…
阅读更多...
主成分分析（PCA）原理详解

主成分分析（PCA）原理详解

转载请声明出处&#xff1a;http://blog.csdn.net/zhongkelee/article/details/44064401 一、PCA简介 1. 相关背景 上完陈恩红老师的《机器学习与知识发现》和季海波老师的《矩阵代数》两门课之后&#xff0c;颇有体会。最近在做主成分分析和奇异值分解方面的项目&#xff0c…
阅读更多...
PCA详解

PCA详解

本文目录 一、来源及作用存在问题基本作用 二、 基本原理及求解步骤核心思想如何选择投影方向 三、原理分析最大投影方差最小重构代价 四、SVD与PCA的关系 一、来源及作用 存在问题 在我们训练模型的过程中&#xff0c;有时会出现在训练集上误差较小&#xff0c;但到了测试集误…
阅读更多...
主成分分析法（PCA）

主成分分析法（PCA）

主成分分析&#xff08;Principal components analysis&#xff0c;以下简称PCA&#xff09;是最重要的降维方法之一。在数据压缩消除冗余和数据噪音消除等领域都有广泛的应用。一般我们提到降维最容易想到的算法就是PCA&#xff0c;下面我们就对PCA的原理做一个总结。 目录 …
阅读更多...
主成分分析（PCA）方法步骤以及代码详解

主成分分析（PCA）方法步骤以及代码详解

主成分分析&#xff08;PCA&#xff09;方法步骤以及代码详解 前言 上一节我们了解到在构建神经网络模型&#xff0c;除了掌握如何搭建神经网络架构&#xff0c;了解参数具体含义&#xff0c;规避风险等方法。第一步是要对采用数据集的详细了解&#xff0c;无需接触任何神经网…
阅读更多...
机器学习——PCA降维（我至今为止遇见的最好的博文）

机器学习——PCA降维（我至今为止遇见的最好的博文）

参考文章&#xff1a;https://zhuanlan.zhihu.com/p/77151308 PCA&#xff08;Principal Component Analysis&#xff09; 是一种常见的数据分析方式&#xff0c;常用于高维数据的降维&#xff0c;可用于提取数据的主要特征分量。 PCA 的数学推导可以从最大可分型和最大重构性…
阅读更多...
通达OA工作流数据报表二次开发版

通达OA工作流数据报表二次开发版

此模块除具备工作流——数据报表所有功能外&#xff0c;新加入的功能包括&#xff1a; 1&#xff1a;查询条件自带可查询未完成的流程&#xff1b; 2&#xff1a;查询条件可设置查询所有子流程的字段&#xff1b; 3&#xff1a;报表可显示流程当前处理人&#xff0c;并且点击每…
阅读更多...
开发通达OA工作流接口从ERP自动生成OA请款单（图文）

开发通达OA工作流接口从ERP自动生成OA请款单（图文）

ERP系统很多不带审批系统&#xff0c;即使有审批系统的话应用起来也不那么容易&#xff0c;因为领导一般都是不使用ERP系统的&#xff0c;那么我就用通达OA来完成ERP的单据审批吧&#xff0c;是不是很酷呢&#xff0c;而且还支持移动端app和微信审批。 ERP端的数据发起由ERP方…
阅读更多...
OA工作流引擎：作为组织血脉支撑的重要性解析

OA工作流引擎：作为组织血脉支撑的重要性解析

前面提到协同OA管理平台是以“人和事”为管理对象&#xff0c;但如何把“人和事”通过一定的方法能全部贯通起来呢。就如同一个人&#xff0c;有手、脚、嘴、头脑等各种器官&#xff0c;但如何能把这些器官充分的调动起来&#xff0c;里面最核心的还是人的血液&#xff0c;OA系…
阅读更多...
通达OA 工作流运行异常情况的紧急处理（图文）

通达OA 工作流运行异常情况的紧急处理（图文）

本文整理自通达OA技术交流群&#xff08;QQ群号&#xff1a;378591362&#xff09;群友交流内容。 一位朋友的工作流设计和运行突然出现故障&#xff0c;显示的数据部分都不正常&#xff0c;如下图&#xff1a; 经过重启所有服务&#xff08;包括缓存服务&#xff09;现象依旧。…
阅读更多...
通达OA二次开发 小飞鱼应用OA工作流二次开发智能公文系统（三）（图文）

通达OA二次开发 小飞鱼应用OA工作流二次开发智能公文系统（三）（图文）

流程流转完毕后&#xff0c;会自动进行归档&#xff0c;默认存成10年存档目录&#xff0c;并且可以在多个存档年限中进行调整切换。点击流程文号可以直接查看具体的流程表单及执行记录。 如果不需要对部门进行管理时&#xff0c;可以直接使用ajax方式快速将存档年限进行修改切换…
阅读更多...
通达OA 工作流流转过程中使用系统自带的提醒功能设置（图文）

通达OA 工作流流转过程中使用系统自带的提醒功能设置（图文）

在流程流转过程中&#xff0c;可以通过增加步骤的方式来提醒相关人员。其实可以使用系统自带的提醒功能&#xff0c;比如需要在某一步骤提醒流程发起人&#xff0c;就可以在提醒设置下设置提醒发起人&#xff0c;有3个选项可选&#xff0c;其中使用手机短信需要短信猫的支持&am…
阅读更多...
通达OA工作流不可编辑

通达OA工作流不可编辑

找到表&#xff1a;flow_run 搜索自增长ID流水号&#xff0c;查看该条记录的用户是否ok 找到表&#xff1a;flow_run_prcs 搜索流水号&#xff1a;run_id*** 查看结果的PRCS_ID数字最大的那一条记录的OP_FLAG是否为1&#xff0c;如果不为1则改为1即可。
阅读更多...
java oa工作流设计_简易OA漫谈之工作流设计（DB）

java oa工作流设计_简易OA漫谈之工作流设计（DB）

1、流程图。 工作流可以做得很复杂&#xff0c;也可以设计的很简单。看下图 看这个图&#xff0c;一个流程图最基础的三部分&#xff1a;流程&#xff0c;步骤&#xff0c;操作。 2、流程模板。 流程图的程序描述就叫流程模板。一个流程模板大概需要的一些属性如下图&#xff1…
阅读更多...
OA审批工作流设计器实现

OA审批工作流设计器实现

OA审批工作流设计器实现 wflow-web&#x1f440;界面一览工作区面板表单管理表单基本设置表单设计器流程设计器 wflow-web 由 Vue ElementUI 驱动&#xff0c;已开源不断更新中 &#xff0c;主要更新 Gitee &#x1f60b; 码云gitee | github地址 &#x1f449; 在线体验地…
阅读更多...
OA工作流引擎设计(纯java开发，不需要额外任何插件引擎)

OA工作流引擎设计(纯java开发，不需要额外任何插件引擎)

目录 1 系统概览 2 表单管理 2.1 添加表单 2.2 表单智能设置 2.2.1 单行文本 2.2.2 多行文本 2.2.3 下拉菜单&#xff0c;单选按钮和复选框 2.2.4 日期时间控件 2.2.5 计算控件 2.2.6 会签字段 2.2.7 员工选择框和部门选择框 2.3 表单测试 2.3.1 可选日期、时间、日…
阅读更多...
OA 系统工作流引擎 Camunda 实践（1）

OA 系统工作流引擎 Camunda 实践（1）

【审核人员看清楚再审核&#xff0c;我是把自己公司的案例分析一下&#xff0c; 这哪是广告&#xff1f;&#xff1f;&#xff1f;】 Camunda是Activiti最大的贡献者之一(除Alfresco以外)&#xff0c;同时也是它一个主 要的执行咨询合作伙伴。camunda表示Activiti可能太拘束于…
阅读更多...
小飞鱼通达二开 OA工作流打印次数统计控制程序（图文）

小飞鱼通达二开 OA工作流打印次数统计控制程序（图文）

每个工作流工作打印了多少次了&#xff0c;在OA里不知道&#xff0c;如何能够控制呢&#xff0c;今天小飞鱼带给大家的就是这个工作量打印次数统计控制程序&#xff0c;使用起来是不是会方便很多。 可以查询打印日志明细。 打印页面上多了一个打印按钮和流水号、打印次数的信息…
阅读更多...
通达OA工作流-表单设计

通达OA工作流-表单设计

第1章 什么是工作流 1.1 工作流的用途 随着企业管理信息化进程的不断深入&#xff0c;协同应用软件的概念已深入人心&#xff0c;而工作流系统正是协同应用软件的核心。通过应用 IT 技术来规范工作流程、提高工作的执行效率和准确度、使企业运营更加高效、规范、稳健&…
阅读更多...
推荐文章

Copyright @ 2022~2023