pca

1 PCAtools

1.1 加载R包

library(PCAtools)
library(tidyverse)

1.2 加载数据，构建表达矩阵和分组信息（以iris为例）

iris <- as.data.frame(iris)
iris <- iris %>% mutate(class = str_c("a",1:dim(iris)[1],sep = ""))
rownames(iris) <- iris$class
iris <- iris[,-6]
head(iris)Sepal.Length Sepal.Width Petal.Length Petal.Width Species
a1          5.1         3.5          1.4         0.2  setosa
a2          4.9         3.0          1.4         0.2  setosa
a3          4.7         3.2          1.3         0.2  setosa
a4          4.6         3.1          1.5         0.2  setosa
a5          5.0         3.6          1.4         0.2  setosa
a6          5.4         3.9          1.7         0.4  setosa# 构建矩阵
expr=iris[c(1,2,3,4)] #  表达矩阵，行是基因，列是样本名
head(expr)Sepal.Length Sepal.Width Petal.Length Petal.Width Species
a1          5.1         3.5          1.4         0.2  setosa
a2          4.9         3.0          1.4         0.2  setosa
a3          4.7         3.2          1.3         0.2  setosa
a4          4.6         3.1          1.5         0.2  setosa
a5          5.0         3.6          1.4         0.2  setosa
a6          5.4         3.9          1.7         0.4  setosa
class <- iris[5] #分组信息，行是样本名，每一列是对应的分组信息
head(class)Species
a1  setosa
a2  setosa
a3  setosa
a4  setosa
a5  setosa
a6  setosa

1.3 表达矩阵标准化

expr <- scale(expr)
head(expr)Sepal.Length Sepal.Width Petal.Length Petal.Width
a1   -0.8976739  1.01560199    -1.335752   -1.311052
a2   -1.1392005 -0.13153881    -1.335752   -1.311052
a3   -1.3807271  0.32731751    -1.392399   -1.311052
a4   -1.5014904  0.09788935    -1.279104   -1.311052
a5   -1.0184372  1.24503015    -1.335752   -1.311052
a6   -0.5353840  1.93331463    -1.165809   -1.048667
#scale 要按样本标准化，默认是按列

1.4 数据转置

expr <-t(expr)  #  表达矩阵，行是基因，列是样本名
expr[,c(1:4)]a1         a2         a3          a4
Sepal.Length -0.8976739 -1.1392005 -1.3807271 -1.50149039
Sepal.Width   1.0156020 -0.1315388  0.3273175  0.09788935
Petal.Length -1.3357516 -1.3357516 -1.3923993 -1.27910398
Petal.Width  -1.3110521 -1.3110521 -1.3110521 -1.31105215

1.4 pca分析

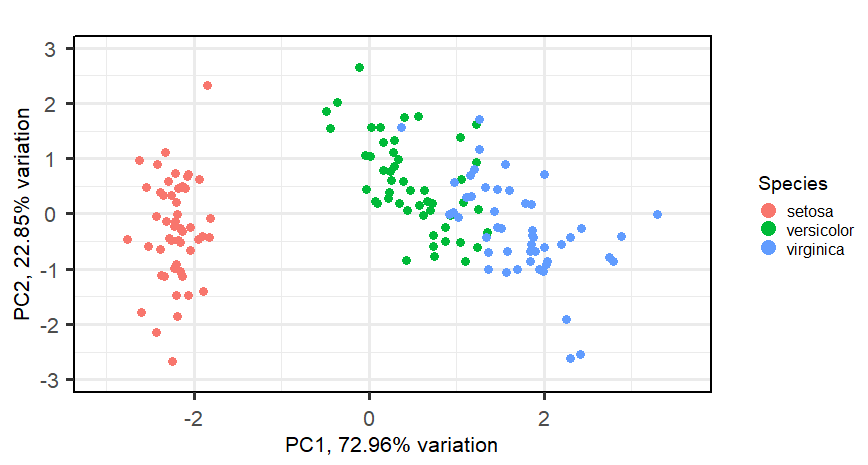
pca <- pca(expr, metadata = class) 
biplot(pca,x="PC1",y="PC2",,colby = "Species",legendPosition = "right",lab = NULL)
# 也可是x="PC1",y="PC3"