背景

本文参考以下两篇平面解析的论文。
《Fast Plane Extraction in Organized Point Clouds Using Agglomerative Hierarchical Clustering》2014 ICRA
《Fast Cylinder and Plane Extraction from Depth Cameras for Visual Odometry》2018 IROS

这两篇论文在为数不多的平面解析中都取得了较好的效果，并且均开源。本文不详细解析论文本身的方法，而是简单的分析代码是如何使用PCA这种方法来拟合平面的。

三点确定一平面

还是回顾一下基础。

平面方程可以由下列两种方式表示。
Ax+By+Cz+D=0 截距式
A(x-x0)+B(y-y0)+C(z-z0)=0 点法式

其中，A、B、C组成的向量为平面的法向量。

为啥呢？

因为平面法向量垂直于平面任何向量，有 ：平面法向量 点乘· 平面向量 = 0 ，对应着 $$A(x-x0)+B(y-y0)+C(z-z0)=0$$
故A,B,C组成的向量为平面法向量。

我们知道，三点可以确定一个平面。假如我们有三个空间点：
$$P_0=(x_0,y_0,z_0)，P_1=(x_1,y_1,z_1)，P_2=(x_2,y_2,z_2)$$
以$P_0$为中心点得到两平面向量：
$$V_0=P_1-P_0,V_1=P_2-P_0$$

平面法向量为：$$n=V_1\times V_2$$

即上面所说的(A,B,C)。

多点拟合平面

基础数学知识

协方差：
$$\begin{array}{rl}Cov(X,Y)& =E[(X-E[X])(Y-E(Y))]\\ & =E[XY]-2E[Y][X]+E[X]E[Y]\\ & =E[XY]-E[X]E[Y]\end{array}$$
协方差矩阵，可描述不同变量关系的矩阵。对角元素是自身的方差，非对角元素是某变量与另一变量的协方差。
$$C={\left(c_{ij}\right)}_{n\times n}=\left(\begin{array}{cccc}{c}_{11}& c_{12}& \cdots & c_{1n}\\ c_{21}& c_{22}& \cdots & c_{2n}\\ \cdot & \cdot & & \cdot \\ \cdot & \cdot & & \cdot \\ \cdot & \cdot & & \cdot \\ c_{n1}& c_{n2}& \dots & c_{nn}\end{array}\right)$$

其中$c_{i}j$为协方差，当i=j时，为方差（对角）。

PCA基本思想

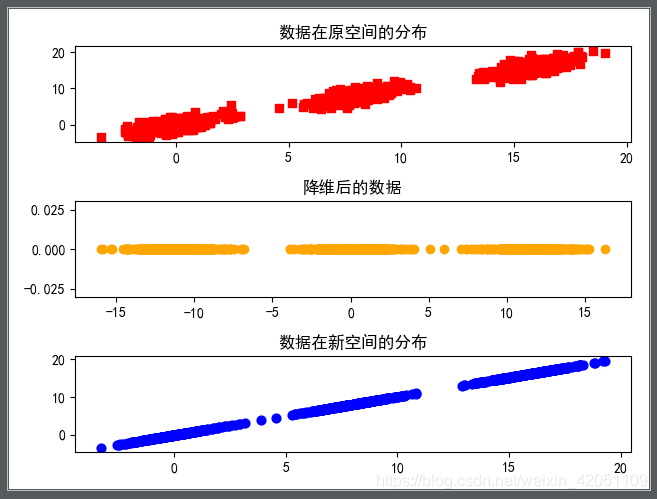
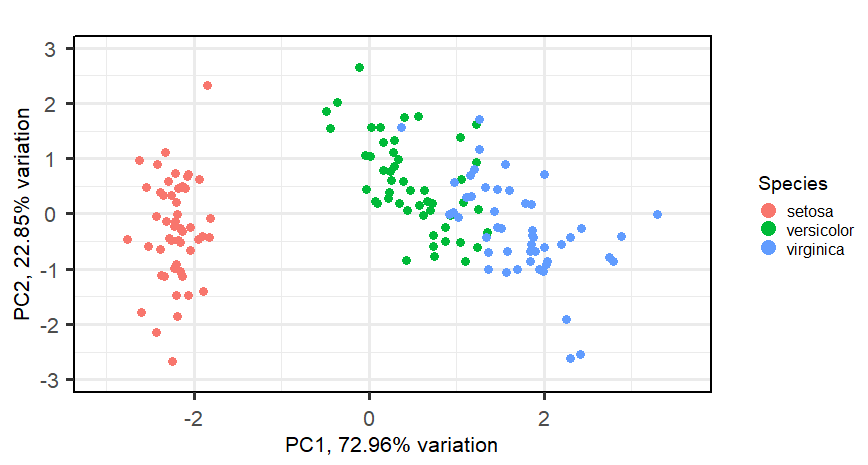
• 将坐标轴中心移到数据的中心（中心化），然后旋转坐标轴，使得数据在C1轴上的方差最大，即全部n个数据个体在该方向上的投影最为分散。意味着更多的信息被保留下来。C1成为第一主成分。
• C2第二主成分：找一个C2，使得C2与C1的协方差（相关系数）为0，以免与C1信息重叠，并且使数据在该方向的方差尽量最大。
• 以此类推，找到第三主成分，第四主成分。。。。第p个主成分。p个随机变量可以有p个主成分。

PCA拟合平面计算过程

我们知道，在三维空间中，空间点的维度为3，要确定一个平面，等同于确定其法向量（三维）。

按照上面PCA的定义，我们同样对三维空间点进行PCA算法操作。
假设当前点数量为N，于是我们拥有N×3个三维空间点。

1.对于三维空间点的数据，先将其均值中心化（mean centering）：
（下图为一个二维中心化例子）
2.然后我们计算所有点在x、y、z轴的均值、方差、协方差、协方差矩阵。
计算公式：

$$\hat{X}=\frac{{\sum }_{i=0}^N{X}_i}{N},\hat{Y}=\frac{{\sum }_{i=0}^N{Y}_i}{N},\hat{Z}=\frac{{\sum }_{i=0}^N{Z}_i}{N}$$
$$Var(X,X)=\frac{{\sum }_{i=1}^N{\left(x_i-\hat{X}\right)}^2}{n}$$
Y,Z方差同理。
$$Cov(X,Y)=\frac{{\sum }_{i=1}^N(x_i-\hat{X})(y_i-\hat{Y})}{n}$$
X、Z的协方差与Y、Z的协方差同理。
最终得到的协方差矩阵为3维。

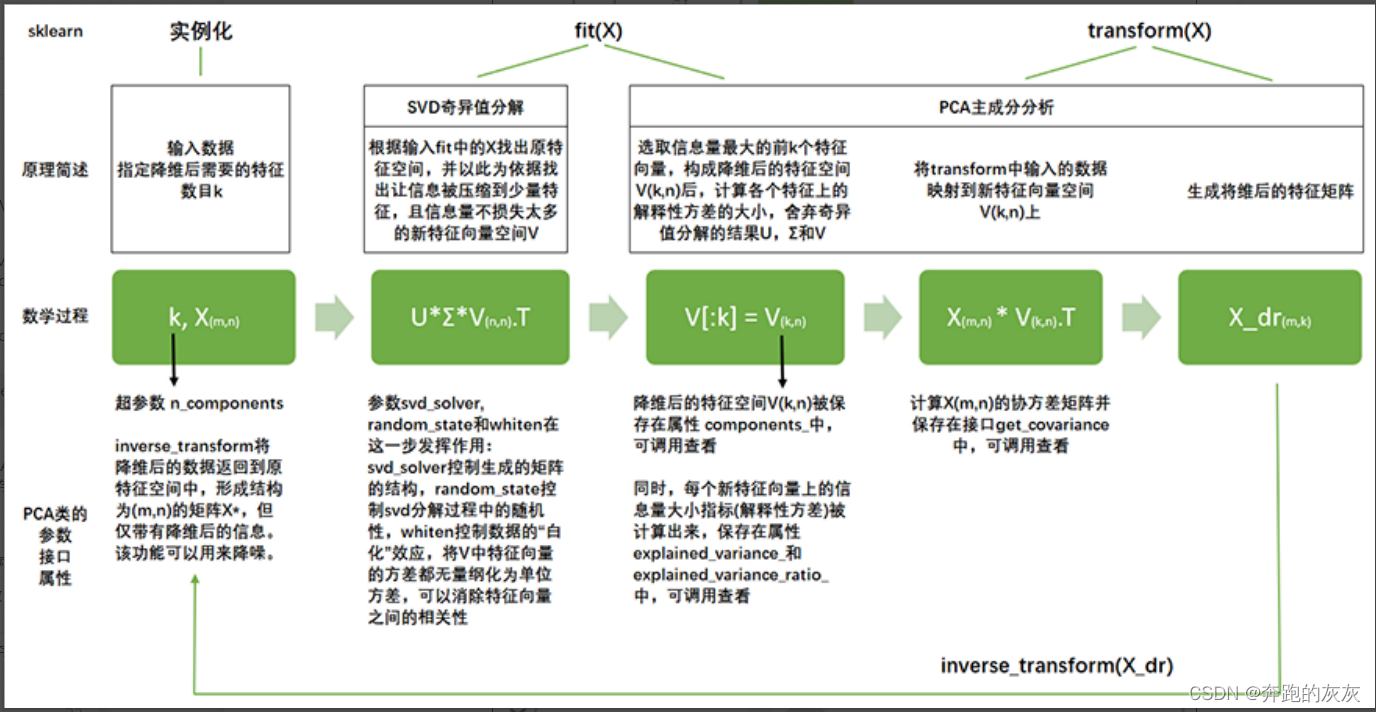
3.计算协方差矩阵特征值与特征向量。
这里就不详细说矩阵的特征值和特征向量是怎么求得了。然后取排名前二特征值对应的特征向量，两特征向量代表着方差较大的基，使两特征向量叉乘，即可得到我们要求的拟合好的平面法向量。

看下图，你会发现最大特征值对应的特征向量方向的点和第二大特征值对应的特征向量方向的点方差较第三大特征值对应的特征向量的点方差大。

从图中，我们应该很好理解，为什么要取前两大特征值的叉乘来获取拟合平面的法向量。实际上我们也可以直接拿最小特征值对应的特征向量来作为平面的法向量。

到这里，我们就基本讲清楚PCA算法的计算步骤，你以为这就完了么？还没，我还没有讲清楚其基本原理，为什么需要中心化？为什么PCA会和协方差矩阵扯上关系？为什么最大特征值对应的特征向量就能代表方差最大的维度？

PCA理解

中心化

我们知道，计算方差和协方差时，需要用到以下公式：
$$Var(X,X)=\frac{{\sum }_{i=1}^N{\left(x_i-\hat{X}\right)}^2}{n}$$
$$Cov(X,Y)=\frac{{\sum }_{i=1}^N(x_i-\hat{X})(y_i-\hat{Y})}{n}$$

假设点集为$P$，中心化即：

$$P_{center}=P-\hat{P}$$

其中$\hat{P}$为三个轴的均值组成的向量。

中心化之后，点集各个轴均值为0，则有以下：

$$Var(X,X)=\frac{{\sum }_{i=1}^N{\left(x_i-0\right)}^2}{n}=\frac{{\sum }_{i=1}^N{x}_i^2}{n}$$
$$Cov(X,Y)=\frac{{\sum }_{i=1}^N(x_i-0)(y_i-0)}{n}=\frac{{\sum }_{i=1}^N{x}_i{y}_i}{n}$$

方便后续计算。

假设有N个三维点，将所有三维点写为3×N的矩阵，有：
$$A=\left(\begin{array}{ccc}{x}_1& y_1& z_1\\ x_2& y_2& z_2\\ x_3& y_3& z_3\\ ...& ...& ...\end{array}\right)$$

其协方差矩阵可简单地表示为：
$$C=\frac{1}{N}\cdot {\left(\begin{array}{ccc}{x}_1& y_1& z_1\\ x_2& y_2& z_2\\ x_3& y_3& z_3\\ ...& ...& ...\end{array}\right)}^T\cdot \left(\begin{array}{ccc}{x}_1& y_1& z_1\\ x_2& y_2& z_2\\ x_3& y_3& z_3\\ ...& ...& ...\end{array}\right)=\frac{1}{N}{A}^{T}A$$

协方差对角化

目前采用的基底为：
$$\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right)$$

协方差矩阵为：
$$\left(\begin{array}{ccc}\frac{1}{N}\sum x_i^2& \frac{1}{N}\sum x_i{y}_i& \frac{1}{N}\sum x_i{z}_i\\ \frac{1}{N}\sum x_i{y}_i& \frac{1}{N}\sum y_i^2& \frac{1}{N}\sum y_i{z}_i\\ \frac{1}{N}\sum x_i{z}_i& \frac{1}{N}\sum y_i{z}_i& \frac{1}{N}\sum z_i^2\end{array}\right)$$

协方差矩阵未必是对角阵，也就是说，在这个基下点的各个轴的分布是相关的（非对角元素不为0）。

正是由于在当前基数据的分布在各个轴（基）协方差不为0，数据的方差没有达到最大，很自然地我们会想到，需要一个新的基底，使得点在新基底的分布在各个轴的分布无关，这个时候，数据的协方差矩阵为对角阵。即各个轴对应的协方差为0。于是，我们就需要把协方差对角化。

点集为$A$，设新的基底为$K$，则点集$A$在新基底的坐标为：$AK$，于是新的协方差矩阵为：
$$D=\frac{1}{N}(AK{)}^T(AK)=\frac{1}{N}{K}^T{A}^{T}AK=K^{T}CK$$
$D$为新的协方差矩阵，且为对角阵。

其中，新的基底K其实就是特征向量，对角阵协方差矩阵D中的各个元素就是特征值。
协方差矩阵中的对角元素，意味着各个基方向数据分布的方差，特征值=方差，特征值越大=方差越大。

而大的特征值对应的特征向量，对应着就是方差大的基/特征方向。

总的来说，特征向量就是新的正交坐标轴，特征值就是所有数据投影到对应特征向量的方差。

在拟合平面这个任务中，其实就是希望找到一个法向量方向，使得所有点投影到这个方向上的方差最小，我们取最小特征值对应的基向量就可以了，而PCA是最大方差理论，原则上这个不属于PCA，但从另一个角度讲，我们可以先提取特征较大的两个基向量，然后使两者叉乘得到平面的法向量，从这个角度讲，这也算是一种PCA的方法，只是需要进行后处理。

参考：
https://stats.stackexchange.com/questions/22329/how-does-centering-the-data-get-rid-of-the-intercept-in-regression-and-pca
https://en.wikipedia.org/wiki/Principal_component_analysis
《Fast Plane Extraction in Organized Point Clouds Using Agglomerative Hierarchical Clustering》
《Fast Cylinder and Plane Extraction from Depth Cameras for Visual Odometry》