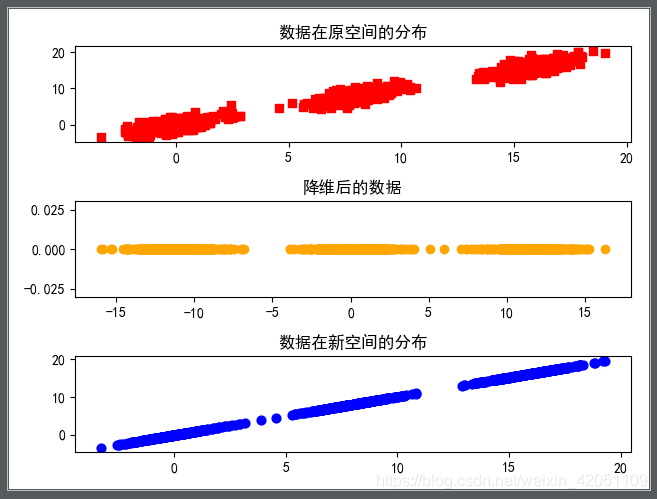
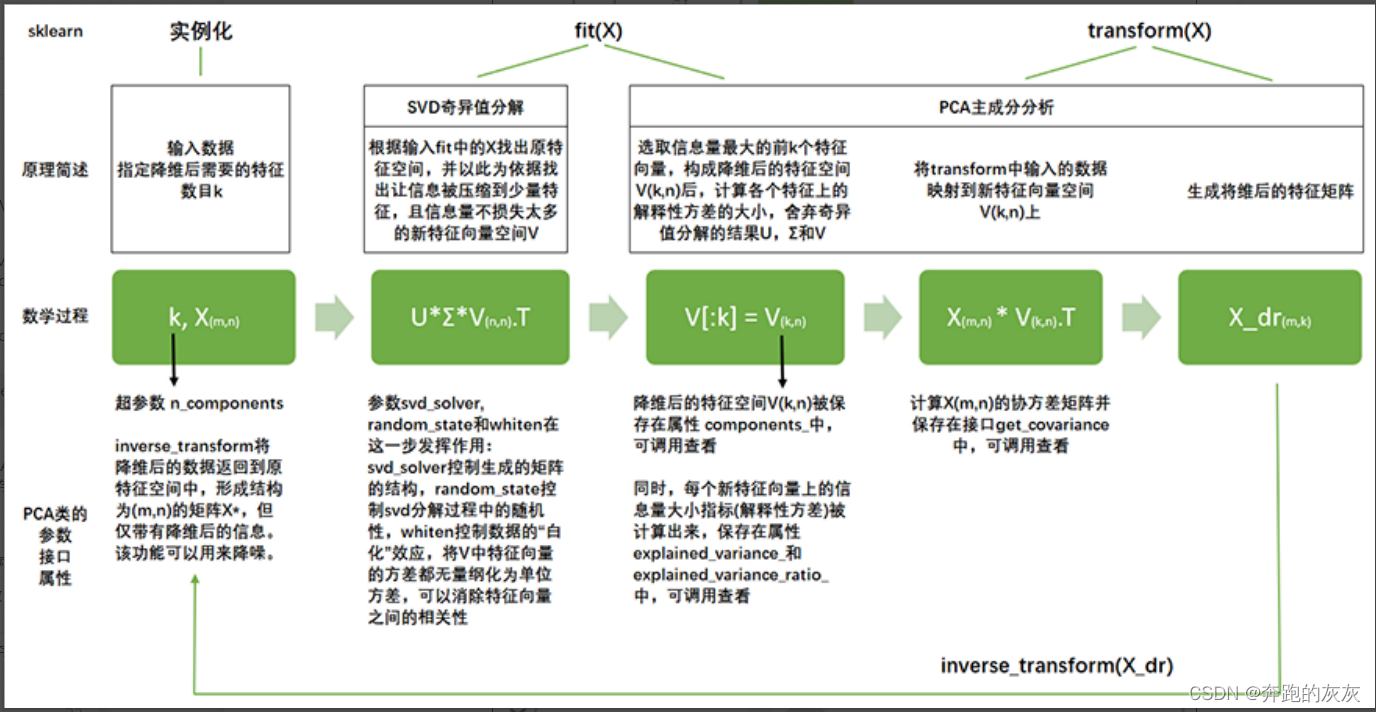
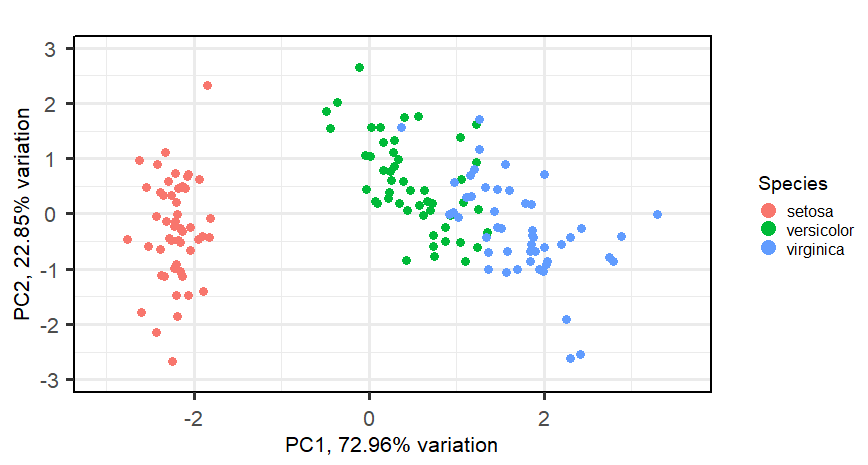
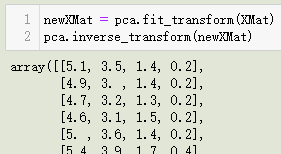
动态PCA方法的核心思想:
将数据X变成增广矩阵,即:
l为潜在变量数,然后对X进行传统的PCA方法进行求解,即是动态PCA的结果。
动态内模PCA与之不同,上述动态PCA的一大缺陷是增加了数据的维度,而动态内模PCA并没有这种问题。
他的核心思想:
其实相当于对tk进行动态分析,这个也是我认为动态内模的核心所在,如果理解错误还望指正。
DIPCA算法流程如下所示:

参考文献:
- Yining Dong and S. Joe Qin. A novel dynamic PCA algorithm for dynamic data modeling and process monitoring[J]. Journal of Process Control, 2018, 67 : 1-11.
- Wenfu Ku and Robert H. Storer and Christos Georgakis. Disturbance detection and isolation by dynamic principal component analysis[J]. Chemometrics and Intelligent Laboratory Systems, 1995, 30(1) : 179-196.