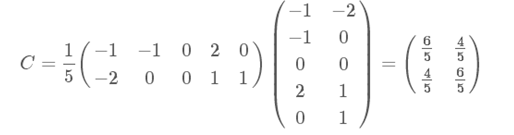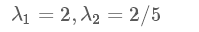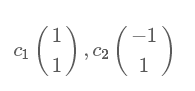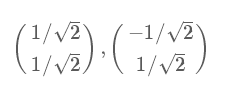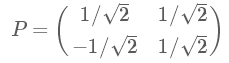PCA算法步骤:
设有m条n维数据。
1)将原始数据按列组成n行m列矩阵X
2)将X的每一行(代表一个属性字段)进行零均值化,即减去这一行的均值
3)求出协方差矩阵![]()
4)求出协方差矩阵的特征值及对应的特征向量
5)将特征向量按对应特征值大小从上到下按行排列成矩阵,取前k行组成矩阵P
6)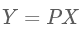
实例:
用PCA方法将这组二维数据其降到一维。
因为这个矩阵的每行已经是零均值,这里我们直接求协方差矩阵:
然后求其特征值和特征向量。得出结果:
特征值:
特征向量:
其中对应的特征向量分别是一个通解,c1和c2可取任意实数。那么标准化后的特征向量为:
因此,矩阵P为:
可以验证协方差矩阵C的对角化:
最后我们用P的第一行乘以数据矩阵,就得到了降维后的表示:
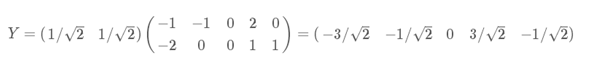
降维投影结果如下图:
以上内容来自https://www.cnblogs.com/mikewolf2002/p/3429711.html
import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import KernelPCA
from sklearn.datasets import make_circles
np.random.seed(0)#使得随机数可预测
x, y = make_circles(n_samples = 400, factor = .3, noise = .05)
kpca = KernelPCA(kernel = 'rbf', gamma = 10)
x_kpca = kpca.fit_transform(x)
plt.figure()
plt.subplot(2, 2, 1, aspect = 'equal')
plt.title("original space")
reds = y == 0
blues = y == 1
plt.plot(x[reds, 0], x[reds, 1], "ro")
plt.plot(x[blues, 0], x[blues, 1], "bo")
plt.xlabel("$x_1$")
plt.ylabel("$x_2$")
plt.subplot(2, 2, 3, aspect = 'equal')
plt.plot(x_kpca[reds, 0], x_kpca[reds, 1], "ro")
plt.plot(x_kpca[blues, 0], x_kpca[blues, 1], "bo")
plt.title("Projection by KPCA")
plt.xlabel("1st principal compontent in space induced by $\phi$")
plt.ylabel("2nd component")
plt.subplots_adjust(0.02, 0.10, 0.98, 0.94, 0.04, 0.35)
plt.show()
np.random.seed()用法
(1) 代码中包含np.random.seed()
import numpy as np
np.random.seed(0)
k = 0
while(k < 4):print(np.random.randn())k += 1在代码中加入np.random.seed()后,不管该段代码运行多少次,输出结果都一致。
结果为:
1.764052345967664
0.4001572083672233
0.9787379841057392
2.240893199201458(2) 代码中不包含np.random.seed()
import numpy as np
k = 0
while(k < 4):print(np.random.randn())k += 1当代码中不包含np.random.seed()时,代码每次运行,运行结果都不一致。
运行结果可以为:
-0.10321885179355784
0.41059850193837233
0.144043571160878
1.454273506962975也可以为:
1.8675579901499675
-0.977277879876411
0.9500884175255894
-0.1513572082976979
结论:当我们设置相同的seed,每次生成的随机数相同
如果不设置seed,则每次会生成不同的随机数