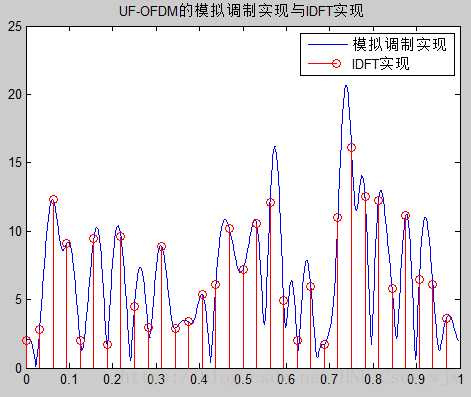
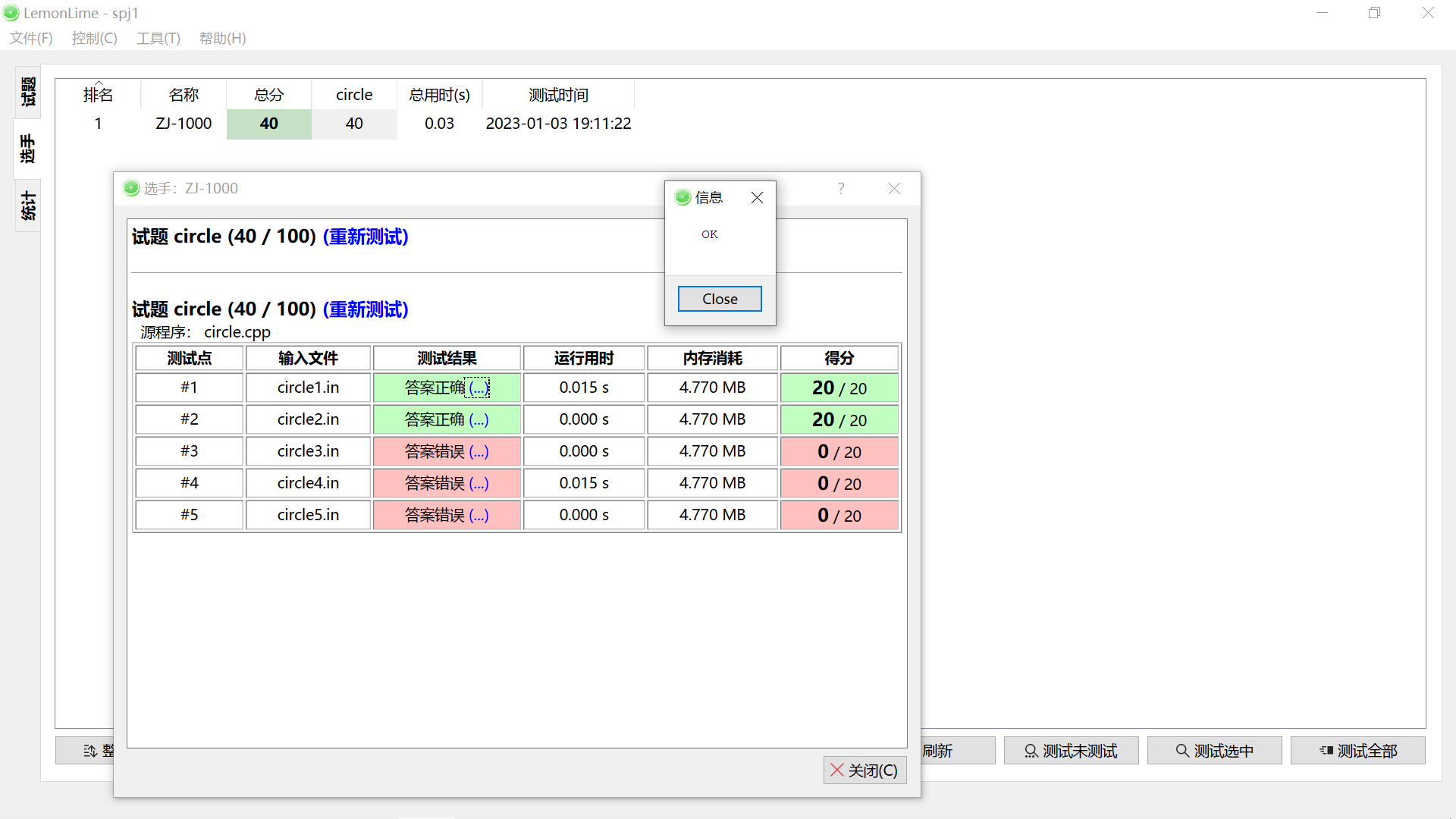
傅里叶变换(DFT)

首先来看看傅里叶(DFT)变换的公式
(1)

FP=\frac {1}{N}\sum_{x=0}^{N-1}\sum_{y=0}^{N-1}P_{x,y}\exp(-j(\frac{2 \pi}{N})(ux+vy))

幅度
(2)

w=\sqrt{u^2+v^2}

其中
u,v代表空间频率，即灰度梯度，梯度由坐标与灰度值求导的向量
w代表 振幅幅度
N代表 灰度像素点总数
Pxy代表 当前像素点灰度
x,y代表 当前像素点的灰度值

在看图像处理的时候可能会很迷茫，作为波形分析的傅里叶变换怎么会有傅里叶变换，图像的傅里叶变换中，T是什么，为什么会有时域？抱着这个问题，先来理解下下面这段话。

图像的频率是表征图像中灰度变化剧烈程度的指标，是灰度在平面空间上的梯
度。傅立叶变换的物理意义是将图像的灰度分布函数变换为图像的频率分布函数，傅

立叶逆变换是将图像的频率分布函数变换为灰度分布函数。

可知，图像是没有事件变化的，只有对x,y轴上的像素变化，与时域对应，叫做图像的空间域。
空间域 (spatial domain) 释义： 又称图像空间(image space)。由图像像元组成的空间。在图像空间中以长度(距离)为自变量直接对像元值进行处理称为空间域处理。
频率域 spatial frequency domain 释义： 以频率(即波数)为自变量描述图像的特征,可以将一幅图像像元值在空间上的变化分解为具有不同振幅、空间频率和相位的简振函数的线性叠加,图像中各种频率成分的组成和分布称为空间频谱。这种对图像的频率特征进行分解、处理和分析称为频率域处理或波数域处理。

初始化定义

#include <stdio.h>
#include <math.h>
#include <time.h>
#include <stdlib.h>
#define VALUE_MAX 255
#define WIDTH 5
#define HEIGHT 5
#define M_PI 3.1415926535897932
struct Complex_{double real;//实部double imagin;//虚部
};
typedef struct Complex_ Complex;

随机数据初始化

int Initdata(double (*src)[WIDTH],int size_w,int size_h){srand((int)time(0));for(int i=0;i<size_w;i++){for(int j=0;j<size_h;j++){src[i][j]=rand()%VALUE_MAX;printf("%lf ",src[i][j]);}printf(";\n");}return 0;
}

2维傅里叶变换函数

//2维傅里叶变换函数
int DFT2D(double (*src)[WIDTH],Complex (*dst)[WIDTH],int size_w,int size_h){for(int u=0;u<size_w;u++){for(int v=0;v<size_h;v++){double real=0.0;double imagin=0.0;for(int i=0;i<size_w;i++){for(int j=0;j<size_h;j++){double I=src[i][j];double x=M_PI*2*((double)i*u/(double)size_w+(double)j*v/(double)size_h);real+=cos(x)*I;imagin+=-sin(x)*I;}}dst[u][v].real=real;dst[u][v].imagin=imagin;if(imagin>=0)printf("%lf+%lfj ",real,imagin);elseprintf("%lf%lfj ",real,imagin);}printf(";\n");}return 0;
}

逆傅里叶变换(IDFT)

2维度逆傅里叶变换函数

//2维逆傅里叶变换函数
int IDFT2D(Complex (*src)[WIDTH],Complex (*dst)[WIDTH],int size_w,int size_h){for(int i=0;i<size_w;i++){for(int j=0;j<size_h;j++){double real=0.0;double imagin=0.0;for(int u=0;u<size_w;u++){for(int v=0;v<size_h;v++){double R=src[u][v].real;double I=src[u][v].imagin;double x=M_PI*2*((double)i*u/(double)size_w+(double)j*v/(double)size_h);real+=R*cos(x)-I*sin(x);imagin+=I*cos(x)+R*sin(x);}}dst[i][j].real=(1./(size_w*size_h))*real;dst[i][j].imagin=(1./(size_w*size_h))*imagin;if(imagin>=0)printf("%lf+%lfj ",dst[i][j].real,dst[i][j].imagin);elseprintf("%lf%lfj ",dst[i][j].real,dst[i][j].imagin);}printf(";\n");}return 0;
}

测试函数

int main() {double src[WIDTH][HEIGHT];Complex dst[WIDTH][HEIGHT];Complex dst_[WIDTH][HEIGHT];Initdata(src, WIDTH, HEIGHT);printf("\n\n");DFT2D(src,dst,WIDTH,HEIGHT);printf("\n\n");IDFT2D(dst,dst_,WIDTH,HEIGHT);
}