IDFT

IDFT(Inverse Discrete Fourier Transform), 傅里叶逆变换，可以将频域信号转换到时域中, 它的公式非常简单：
$$x[n]=\frac{1}{N}\sum _{k=0}^{N-1}X[k]e^{j2\pi kn/N}$$

$X[k]$：离散频率下标为k时的频率大小

$x[n]$: 离散时域信号序列

$N$: 信号序列的长度，也就是采样的个数

对比我们之前讲过的DFT，两者公式类似，但是注意在DFT中指数带负号，而IDFT中不带

从矩阵的角度看IDFT

DFT的矩阵表示

讲IDFT之前，我们先复习DFT的矩阵表示形式：
$$\left[\begin{array}{cccc}{s}_0^0& s_0^1& \cdots & s_0^{N-1}\\ ⋮& ⋮& ⋮& ⋮\\ s_k^0& s_k^1& \cdots & s_k^{N-1}\\ ⋮& ⋮& \ddots & ⋮\\ s_{N-1}^0& s_{N-1}^1& \cdots & s_{N-1}^{N-1}\end{array}\right]\left[\begin{array}{c}x[0]\\ x[1]\\ ⋮\\ x[n]\\ ⋮\\ x[N-1]\end{array}\right]=\left[\begin{array}{c}X[0]\\ X[1]\\ ⋮\\ X[k]\\ ⋮\\ X[N-1]\end{array}\right]$$
$S$矩阵中的每一行都是一个$S_k$向量，$S_k=e^{-j2\pi kn/N},n=0,1,\cdots ,N-1$，进一步简化上面的表示，得到：
$$\left[\begin{array}{ccc}\cdots & S_0& \cdots \\ & ⋮& \\ \cdots & S_k& \cdots \\ & ⋮& \\ \cdots & S_{N-1}& \cdots \end{array}\right]\left[\begin{array}{c}x[0]\\ x[1]\\ ⋮\\ x[n]\\ ⋮\\ x[N-1]\end{array}\right]=\left[\begin{array}{c}X[0]\\ X[1]\\ ⋮\\ X[k]\\ ⋮\\ X[N-1]\end{array}\right]$$

IDFT的矩阵表示

从IDFT的公式，可以看出，其实IDFT和DFT表示是一样的，只是对象发生了变化。具体来说，有两个变化：

• 由于指数部分不再有符号，$S_k$进行了共轭操作，得到$S_k^{\ast }$
• 输入是频率信息X[k]

因此，矩阵表示变成了下面这样：
$$\left[\begin{array}{ccc}\cdots & S_0^{\ast }& \cdots \\ & ⋮& \\ \cdots & S_k^{\ast }& \cdots \\ & ⋮& \\ \cdots & S_{N-1}^{\ast }& \cdots \end{array}\right]\left[\begin{array}{c}X[0]\\ X[1]\\ ⋮\\ X[n]\\ ⋮\\ X[N-1]\end{array}\right]=\left[\begin{array}{c}x[0]\\ x[1]\\ ⋮\\ x[k]\\ ⋮\\ x[N-1]\end{array}\right]$$

Talk is cheap, show me the code

接下来就简单多了，我们将先介绍如何使用scipy中ifft，然后自己动手实现一份ifft

导入必要的包

import numpy as np
from scipy.fftpack import fft, ifftimport matplotlib.pyplot as plt%matplotlib notebook

生成信号用于测试

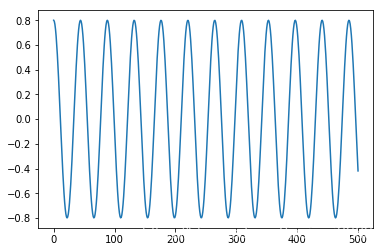
def generate_sine(N, A, fs, f0, phi):'''N : number of samplesA : amplitudefs: sample ratef0: frequencyphi: initial phase'''T = 1/fsn = np.arange(N)x = A*np.cos( 2*np.pi*f0*n*T + phi )return x# generate signal
N = 501
A = 0.8
fs = 44100
f0 = 1000
phi = 0.0x = generate_sine(N, A, fs, f0, phi)plt.figure()
plt.plot(x)
plt.show()

使用scipy中的ifft

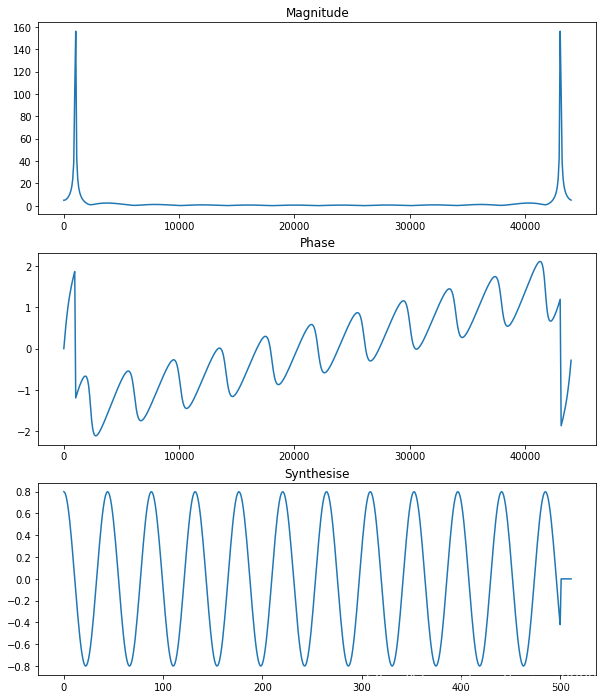
# fft the signal
N = 512                       # fft size
X = fft(x, N)
mX = np.abs(X)
pX = np.angle(X)freq_axis = np.arange(N)/N * fs
plt.figure(figsize=(10, 12))
ax = plt.subplot(3,1,1)
plt.plot(freq_axis, mX)
ax.set_title('Magnitude')ax = plt.subplot(3,1,2)
plt.plot(freq_axis, pX)
ax.set_title('Phase')# ifft it
ifft_x = ifft(X)
ax = plt.subplot(3,1,3)
plt.plot(ifft_x)
ax.set_title('Synthesise')plt.show()

自己动手写ifft

只有两个地方要注意：

• 不要忘记乘上 1/N
• $S_k^{\ast }$是$S_k$向量的共轭后的结果。反映在代码中，就是$S_k^{\ast }$不要共轭操作之间返回

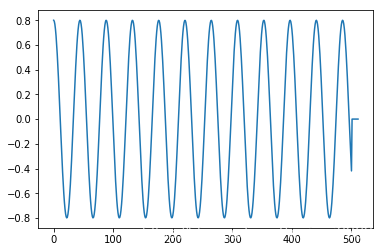
def generate_complex_sinusoid(n, N):'''n : time index (or frequency index)N : number of sample'''k = np.arange(N)c_sin = np.exp(1j*2*np.pi*k*n/N)return c_sin# ifft loop
ifft_x = np.array([])for i in range(N):s = generate_complex_sinusoid(i, N)ifft_x = np.append(ifft_x, 1/N * np.sum(X*s))plt.figure()
plt.plot(ifft_x)
plt.show()

总结

通过自己动手，我们发现IDFT的原来和实现很简单，几乎与DFT一模一样，唯一需要注意的点就是$S_k^{\ast }$