1. 定义

上一篇研究了Matlab如何进行离散傅里叶变换DFT(快速傅里叶变换FFT)进行频谱分析。工程上我们还会遇到这样的问题：获取了信号的频谱，希望从信号的频谱来恢复时域信号。这一篇来研究如何进行利用离散傅里叶逆变换（iDFT）从频谱中恢复时域信号。
离散傅里叶逆变换 (iDFT)的定义为：

$x(n)=\mathrm{i}\mathrm{D}\mathrm{F}\mathrm{T}[X(k)]=\frac{1}{N}\sum _{k=0}^{N-1}X(k)e^{j\frac{2\pi }{N}nk}$, $0\le n\le N-1$
式中，$x(n)$为时域离散采样序列（通常为实数序列），$N$为时域离散采样序列$x(n)$的长度，$X(k)$为频域离散采样序列（通常为复数序列）。

也存在快速傅里叶逆变换（iFFT）来实现iDFT的快速算法，其主要作用也是减小计算量、节约计算资源、便于在线计算。

2. 变换和处理

Matlab软件自带ifft函数实现快速傅里叶逆变换算法，与上一篇DFT变换一样，要想从频谱恢复时域信号，也需要解决以下问题（建议与上一篇对应起来看）：

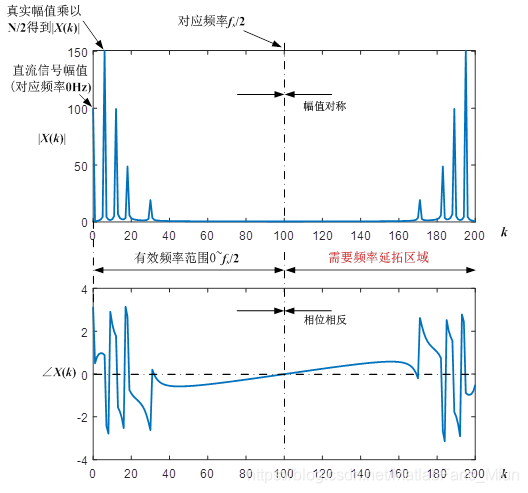
a) 幅值变换：真实频谱幅值乘以$N/2$得到频谱序列$X(k)$的幅值$|X(k)|$；
b) 频谱延拓：真实频谱的频率范围为$0-f_s/2$，而参与iDFT变换的频谱序列$X(k)$为两部分共轭复数序列组成，因此需要对物理频谱进行延拓得到$X(k)$。频谱延拓的方案上图所示。
c) 直流信号的处理：直流信号幅值乘以2，再进行幅值变换乘以$N/2$，得到频谱序列$X(k)$的直流分量$|X(0)|$。

3. 函数

作者在Matlab软件自带ifft函数的基础上，使用Matlab开发了函数iDFT.m，通过函数来实现上述幅值变换、频谱延拓和直流信号的处理，能够直接从从频谱恢复时域信号，函数简单、易用、通用性好。

function [xn,t] = iDFT(X_m,X_phi,ts,drawflag)
% [xn,t] = iDFT(X_m,X_phi,ts) 离散序列的快速傅里叶逆变换，频域转换为时域信号
% 输入 X_m为幅值向量
%      X_phi为相位向量，单位为°
%      ts为序列的采样时间/s
%      drawflag为绘图标识位，取0时不绘图，其余非0值时绘图，默认为绘图
% 输出  xn为离散序列向量
%       t为与xn对应的时间向量
% 注意计算出来的0频分量在进行ifft计算时，幅值应乘以2
% By ZFS@wust  2020
% 获取更多Matlab/Simulink原创资料和程序，清关注微信公众号：Matlab Fans

4. 实例演示

下面结合实例进行演示和分析。

例1：单频正弦信号（整数周期采样）

%% Eg 1 单频正弦信号
ts = 0.01;
t = 0:ts:1;
A = 1.5;       % 幅值  
f = 2;         % 频率
w = 2*pi*f;    % 角频率
phi = pi/3;    % 初始相位 
x = A*cos(w*t+phi);   % 时域信号
figure
plot(t,x)
xlabel('时间/s')
ylabel('时域信号x(t)')
% DFT变换将时域转换到频域,并绘制频谱图
[f,X_m,X_phi] = DFT(x,ts);
% iDFT逆变换将频域转换到时域,并绘制时域图
[xn,t2] = iDFT(X_m,X_phi,ts);
hold on
plot(t,x,'r--')
legend('恢复的时域信号','原始时域信号')

结果：

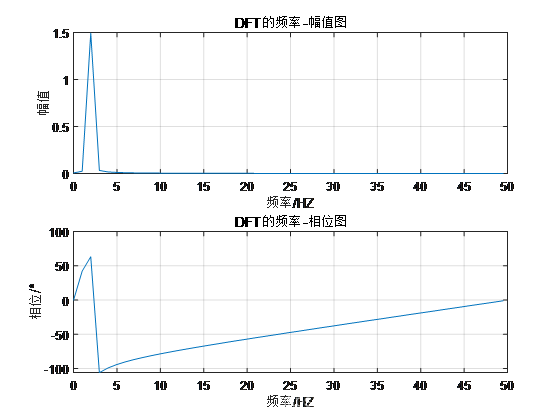
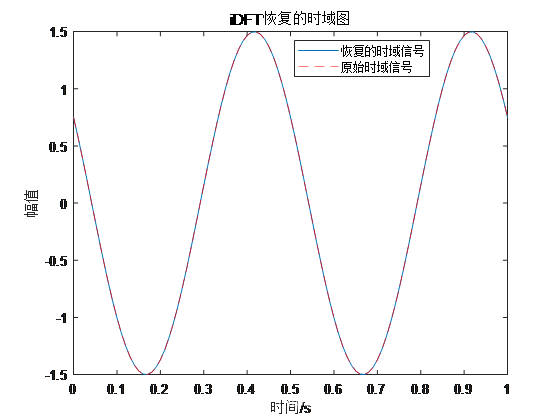
例2：含有直流分量的单频正弦信号

%% Eg 2 含有直流分量的单频正弦信号
ts = 0.01;
t = 0:ts:1;
A = 1.5;       % 幅值  
f = 5;         % 频率
w = 2*pi*f;    % 角频率
phi = pi/6;    % 初始相位 
x = 0.5 + A*cos(w*t+phi);   % 时域信号,带有直流偏移0.5
figure
plot(t,x)
xlabel('时间/s')
ylabel('时域信号x(t)')
% DFT变换将时域转换到频域,并绘制频谱图
[f,X_m,X_phi] = DFT(x,ts);
% iDFT逆变换将频域转换到时域,并绘制时域图
[xn,t2] = iDFT(X_m,X_phi,ts);
hold on
plot(t,x,'r--')
legend('恢复的时域信号','原始时域信号')

结果：

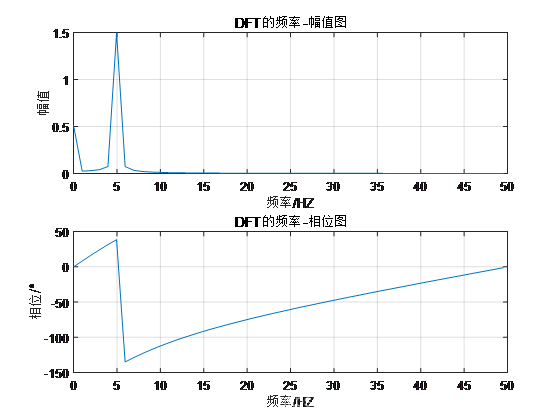
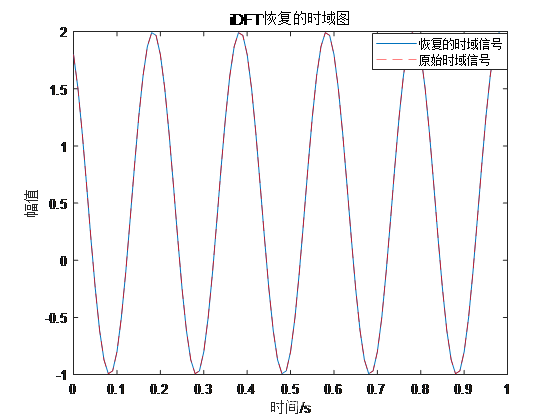
例3：正弦复合信号

%% Eg 3 正弦复合信号
ts = 0.01;
t = 0:ts:2;
A = [1.5 1 0.5 0.2];    % 幅值  
f = [3 6 9 15];         % 频率
w = 2*pi*f;             % 角频率
phi = (1:4)*pi/4;       % 初始相位 
x = -0.5 + A(1)*cos(w(1)*t+phi(1)) + A(2)*cos(w(2)*t+phi(2)) + A(3)*cos(w(3)*t+phi(3)) + A(4)*cos(w(4)*t+phi(4));     % 时域信号
figure
plot(t,x)
xlabel('时间/s')
ylabel('时域信号x(t)')
% DFT变换将时域转换到频域,并绘制频谱图
[f,X_m,X_phi] = DFT(x,ts);
% iDFT逆变换将频域转换到时域,并绘制时域图
[xn,t2] = iDFT(X_m,X_phi,ts);
hold on
plot(t,x,'r--')
legend('恢复的时域信号','原始时域信号')

结果：

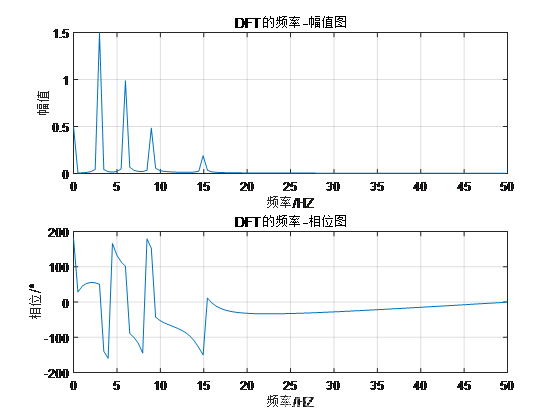
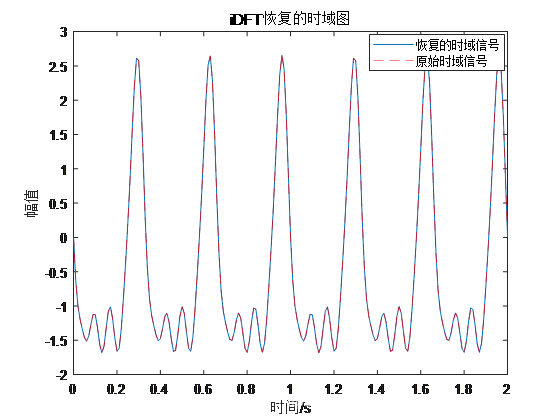
例4：含有随机干扰的正弦信号

%% Eg 4 含有随机干扰的正弦信号
ts = 0.01;
t = 0:ts:2;
A = [1 0.5];    % 幅值  
f = [3 10];         % 频率
w = 2*pi*f;             % 角频率
phi = (1:2)*pi/3;       % 初始相位 
x =  A(1)*cos(w(1)*t+phi(1)) + A(2)*cos(w(2)*t+phi(2)) + 0.8*(rand(size(t))-0.5);     % 时域信号
figure
plot(t,x)
xlabel('时间/s')
ylabel('时域信号x(t)')
% DFT变换将时域转换到频域,并绘制频谱图
[f,X_m,X_phi] = DFT(x,ts);
% iDFT逆变换将频域转换到时域,并绘制时域图
[xn,t2] = iDFT(X_m,X_phi,ts);
hold on
plot(t,x,'r--')
legend('恢复的时域信号','原始时域信号')

结果：

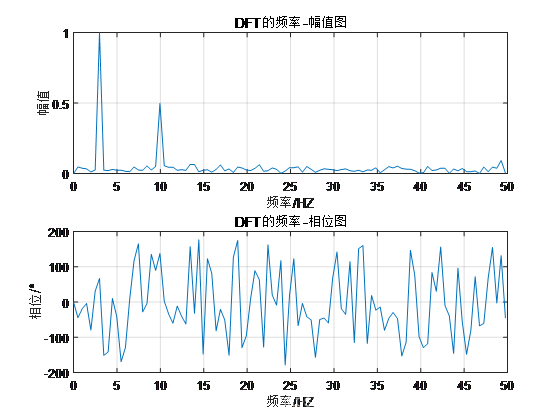
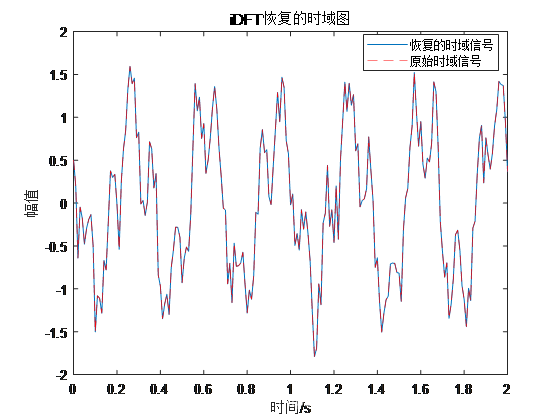
例5：实际案例

%% Eg 5 实际案例
load data
ts = 0.001;
x = Jsd;
t = [0:length(x)-1]*ts;
figure
plot(t,x)
xlabel('时间/s')
ylabel('时域信号x(t)')
% DFT变换将时域转换到频域,并绘制频谱图
[f,X_m,X_phi] = DFT(x,ts);
% iDFT逆变换将频域转换到时域,并绘制时域图
[xn,t2] = iDFT(X_m,X_phi,ts);
hold on
plot(t,x,'r--')
legend('恢复的时域信号','原始时域信号')

结果：

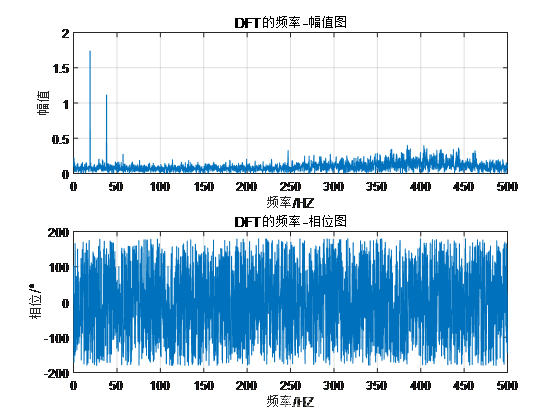
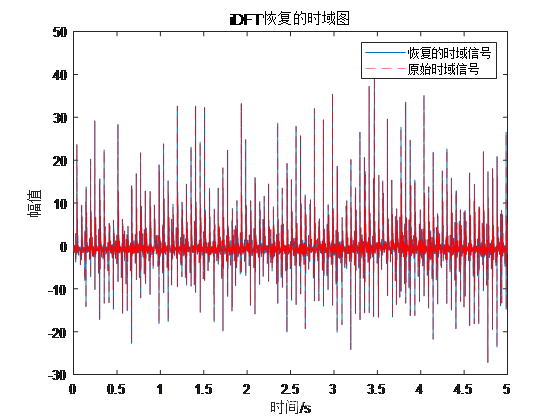
上述各例中，通过iDFT恢复的时域信号与原始信号完全重合，说明利用离散傅里叶逆变换（iDFT）可以从频谱恢复时域信号。

5. 联系作者

有Matlab/Simulink方面的技术问题，欢迎发送邮件至944077462@qq.com讨论。
更多Matlab/Simulink原创资料，欢迎关注微信公众号：Matlab Fans

源程序下载:
1. csdn资源: Matlab如何进行离散傅里叶变换DFT(快速傅里叶变换FFT)进行频谱分析
2. 扫码关注微信公众号Matlab Fans，回复BK07获取百度网盘下载链接。