DFT与IDFT
一.方法简介
序列x(n)(n=0,1,…N-1)的DFT定义为
X ( k ) = ∑ n = 0 N − 1 x ( n ) e − j 2 π n k N X(k)=\sum_{n=0}^{N-1}x(n)e^{-j\frac{2\pi nk}{N}} X(k)=n=0∑N−1x(n)e−jN2πnk
设 x ( n ) = a ( n ) + j b ( n ) , X ( k ) = A ( k ) + j B ( K ) , Q = 2 π / N 设x(n)=a(n)+jb(n),\quad X(k)=A(k)+jB(K),\quad Q=2\pi/N 设x(n)=a(n)+jb(n),X(k)=A(k)+jB(K),Q=2π/N
则上式变为:
A ( k ) + j B ( k ) = ∑ n = 0 N − 1 [ a ( n ) + j b ( n ) ] [ cos ( Q n k ) − j sin ( Q n k ) ] A(k)+jB(k)=\sum_{n=0}^{N-1}[a(n)+jb(n)][\cos(Qnk)-j\sin(Qnk)] A(k)+jB(k)=n=0∑N−1[a(n)+jb(n)][cos(Qnk)−jsin(Qnk)]
即
A ( k ) = ∑ n = 0 N − 1 [ a ( n ) cos ( Q n k ) + b ( n ) sin ( Q n k ) ] A(k)=\sum_{n=0}^{N-1}[a(n)\cos(Qnk)+b(n)\sin(Qnk)] A(k)=n=0∑N−1[a(n)cos(Qnk)+b(n)sin(Qnk)]
B ( k ) = ∑ n = 0 N − 1 [ b ( n ) cos ( Q n k ) − a ( n ) sin ( Q n k ) ] B(k)=\sum_{n=0}^{N-1}[b(n)\cos(Qnk)-a(n)\sin(Qnk)] B(k)=n=0∑N−1[b(n)cos(Qnk)−a(n)sin(Qnk)]
序列X(k)的IDFT定义为:
x ( n ) = 1 N ∑ k = 0 N − 1 X ( k ) W N − n k , n = 0 , 1 , . . . N − 1 x(n)=\frac{1}{N}\sum_{k=0}^{N-1}X(k)W_{N}^{-nk},\quad n=0,1,...N-1 x(n)=N1k=0∑N−1X(k)WN−nk,n=0,1,...N−1
它 与 D F T 的 区 别 在 于 将 W N 改 变 为 改 变 为 W N − 1 , 并 多 了 一 个 除 以 N 的 运 算 , 公 式 如 下 它与DFT的区别在于将W_{N}改变为改变为W_{N}^{-1},并多了一个除以N 的运算,公式如下 它与DFT的区别在于将WN改变为改变为WN−1,并多了一个除以N的运算,公式如下
a ( n ) = 1 N ∑ k = 0 N − 1 [ A ( k ) cos ( Q n k ) − B ( k ) sin ( Q n k ) ] a(n)=\frac{1}{N}\sum_{k=0}^{N-1}[A(k)\cos(Qnk)-B(k)\sin(Qnk)] a(n)=N1k=0∑N−1[A(k)cos(Qnk)−B(k)sin(Qnk)]
b ( n ) = 1 N ∑ k = 0 N − 1 [ B ( k ) cos ( Q n k ) + A ( k ) sin ( Q n k ] b(n)=\frac{1}{N}\sum_{k=0}^{N-1}[B(k)\cos(Qnk)+A(k)\sin(Qnk] b(n)=N1k=0∑N−1[B(k)cos(Qnk)+A(k)sin(Qnk]
二.编程实现
考滤到DFT和IDFT算法过程中有部分相似,可以把它们合成到一个算法。
DFT.c
/*x-存放要变换数据的实部y-存放要变换数据的虚部a-存放变换结果的实部b-存放变换结果的虚部n-数据长度sign-为1时执行DFT,为-1时执行IDFT
*/
#include "math.h"
void dft(x,y,a,b,n,sign)
int n, sign;
double x[],y[],a[],b[];
{int i,k;double c,d,q,w,s;q = 6.28318530718/n;for (k=0;k<n;k++){w=k*q;a[k]=b[k]=0.0;for(i=0;i<n;i++){d=i*w;c=cos(d);s=sin(d)*sign;a[k]+=c*x[i] + s*y[i];b[k]+=c*y[i] - s*x[i];}}if(sign == -1){c=1.0/n;for (k=0;k<n;k++){a[k]=c*a[k];b[k]=c*b[k];}}
}
下面验证此算法,对X(n)=(0,1,2,3,4,5,6,7),做DFT和IDFT算法
dft_d.c
#include "stdio.h"
#include "math.h"
#include "dft.c"
#define N 4
static double x[N],y[N],a[N],b[N],c[N];
main(){int k;int i=0;for(i=0; i<N; i++){x[i]=i;y[i]=0;}dft(x,y,a,b,N,1); //DFT变换for(i=0; i<N; i++){c[i]=sqrt(a[i]*a[i]+b[i]*b[i]); //算出模printf("%lf + j %lf \n",a[i],b[i]);//输出变换后结果 printf("%lf \n",c[i]); //输出模值printf("\n"); }dft(a,b,x,y,N,-1); //IDFT变换for(i=0; i<N; i++){printf("%lf \n",x[i]); //输出x(n)的实部}}
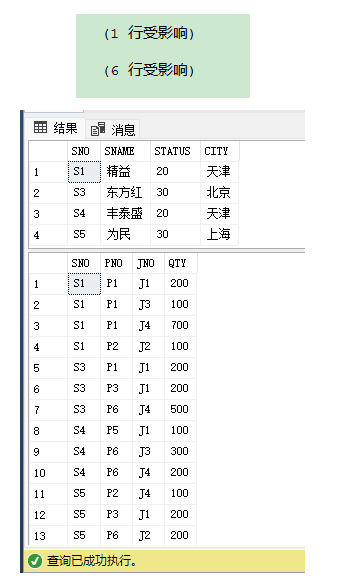
运行结果:

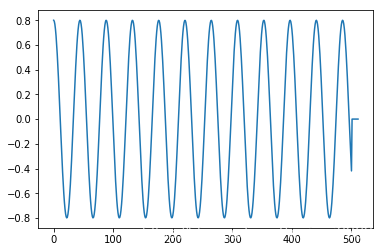


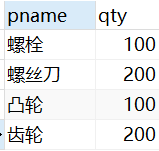
![数据库---[复习2]---数据查询---设有一个SPJ数据库,包括S、P、J及SPJ4个关系模式··· ···](https://img-blog.csdnimg.cn/2020122421232856.gif#pic_center)





![浅谈online judge平台 spj [special judge] 使用 | 修改问题](https://img-blog.csdnimg.cn/5c42bb7c0c2c43329652a95ca7378160.png)