这是本系列的最后一章，原先计划是把这部分内容一并挪到上一章里的，不过喜欢凑一个整数，而且想骗一点流量，所以把它们拆成了两部分。我们在前面的内容中，通过使用不同的频率信号对原始信号进行采样，从而分析出原始波形的频率组成。
我们通过离散傅里叶DFT计算出频率后，经过处理后，有时候还是有需要将频率转换回时域信号。虽然这个部分也不是什么困难的事，作为这个系列的收尾，我还是提供它的1维的逆计算代码实现。

前期准备

复平面空间

虽然我已经在前面的文章里提到过复平面空间，对于一个向量来说，它在复平面上存在着和它实数部相同，虚数部相反的另一个向量，这个称为共轭。

由于我们的数据经过傅里叶变换后，全部变成了在复平面表示，所以在求解出 $C_k$ 数组后，我们要做的一个工作就是把复数重新映射到实数平面。为了方便计算，我们把全部复数，以复平面上的向量进行表示，那么对于原函数 $f(x)$ 来说，对于某一点 $x_o$ 上的振幅，就可以表示为该点在复平面上的向量的模，即：

$$amplitude(x_o)=\sqrt{a^2+b^2}$$

而该点在原函数上处于正区间还是负区间，则与该点在复平面上映射的实数轴的正负号是一致的。所以，如果试图绘制原函数，那么我们唯一缺少的就是它在X轴上的长度，即时间 $t$。

所幸，时间 $t$ 与我们定义的采样率相关，即DFT函数里指数部分的 $2\pi kn/N$。也就是说，如果DFT 长度为100，采样率为100Hz，那么原函数在X轴上也有100个点。

iDFT基本公式

$$f(x)=\frac{1}{N}\Sigma F(k)e^{2j\pi kn/N}$$

复数乘法

观察离散傅里叶函数 $f(x)=\frac{1}{N}\Sigma F(k)e^{2j\pi kn/N}$，其核心部分就是 $F(k)$ 和 $e^{2j\pi kn/N}$ ，这里的$F(k)$ 也就是 $C_k$ 我们前面章节程序求解出的复数数组。而 $e^{2j\pi kn/N}$ 用欧拉公式展开后，

$$e^{2j\pi kn/N}=cos(2\pi kn/N)+jsin(2\pi kn/N)$$

通过带入不同的$k$，也就是采样频率后，也会得到一组复数数组。所以这里可以用到矩阵乘法，也可以逐项的使用复数乘法直接计算，复数乘法的运算法表示如下：

$$\vec{A}\cdot \vec{B}=(a,bj)(c,dj)=ac-bd+(ad+cb)j$$

基信号

傅里叶的本质是有一组不同频率的基信号加和而成。而基信号由公式 $s(x_o)=C_k\cdot e^{\omega }$ 描述，你可以采用两种不同的方式构成这个信号，一种是基于欧拉坐标系，以给定实数轴长度，然后根据 $C_k$ 贡献值，生成新的基信号；

另一种是比较常见的，基于极坐标的方式，生成基信号。

不论你使用哪一种方法，我的建议是最好重构信号的过程，与频率分析的过程一致，因为一个细微的疏忽，你会得到完全不一样的答案。

在上一章的代码中，我采用的是基于极坐标的方式生成 $C_k$，那么基于这一原则，我们就采用逆过程，重新生成基信号。

实现代码

基信号实现

def calculate_base_fx(Ck, freq, N):pi = np.pi  # pik = freq  # sampling frequencysig_cos = []sig_sin = []for n in range(N):  # x(0), x(1), x(2), ... x(N)r_sig = cos(2 * pi * n * k / N)i_sig = sin(2 * pi * n * k / N)real, imag = complex_multi(r_sig, i_sig, Ck.real, Ck.imag)# reconstruct signalssig_cos.append(real)sig_sin.append(imag)return sig_cos, sig_sin

这一块代码我不做过多解释，它实现的功能，即基信号的生成：

$$e^{2j\pi kn/N}=cos(2\pi kn/N)+jsin(2\pi kn/N)$$

信号叠加

def idft_1d(dft):N = len(dft)freq_real, freq_imag = np.zeros(N), np.zeros(N)maximum_sampling_freq = N  # 希望使用的采样最大频率increased_sampling_freq = maximum_sampling_freq / N  # 采样率步进current_sampling_freq = 0  # 当前的采样率，从 0Hz 开始进行采样for ck in dft:fxc, fxs = calculate_base_fx(ck, current_sampling_freq, N)# sigma all basis frequenciesfreq_real = freq_real + np.array(fxc)freq_imag = freq_imag + np.array(fxs)# increase freqcurrent_sampling_freq = current_sampling_freq + increased_sampling_freqreturn freq_real / N, freq_imag / N

这一部执行完毕后，我们会得到原始信号，但是是在复平面上的表达，所以接下来要增加一个简单的过程，把信号映射到实数平面上。

实数平面映射

def reconstruct(real, imag):signal = []for i in range(len(real)):# compute amplitudeamp = np.sqrt(real[i] ** 2 + imag[i] ** 2)if real[i] < 0:signal.append(-amp)else:signal.append(amp)return signal

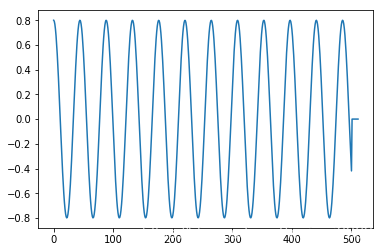
至此，信号复原完毕，然后我们检查一下输出：

    _axis, _signal = generate_original_signals(50) # 生成长度50的原始信号_dft = dft_1d(_signal) # 使用之前的dft函数，对信号频率进行解析_real, _imag = idft_1d(_dft)  # 执行逆计算，重构信号_re_sig = reconstruct(_real, _imag)  # 把原始信号映射到实数平面validate_idft(_signal, _re_sig)  # 验证结果

输出

pt:0    sig:    0.0             res:    0.0             var     0.0
pt:1    sig:    1.1623          res:    1.1623          var     0.0
pt:2    sig:    1.5515          res:    1.5515          var     0.0
pt:3    sig:    1.0498          res:    1.0498          var     0.0
pt:4    sig:    0.2424          res:    0.2424          var     0.0
pt:5    sig:    -0.1726         res:    -0.1726         var     0.0
pt:6    sig:    -0.0364         res:    -0.0364         var     0.0
pt:7    sig:    0.1802          res:    0.1802          var     0.0
pt:8    sig:    -0.0831         res:    -0.0831         var     0.0
pt:9    sig:    -0.8452         res:    -0.8452         var     0.0
pt:10   sig:    -1.4958         res:    -1.4958         var     0.0
pt:11   sig:    -1.351          res:    -1.351          var     0.0
pt:12   sig:    -0.3271         res:    -0.3271         var     0.0
pt:13   sig:    0.9217          res:    0.9217          var     0.0
pt:14   sig:    1.5475          res:    1.5475          var     0.0
pt:15   sig:    1.2347          res:    1.2347          var     0.0
pt:16   sig:    0.4294          res:    0.4294          var     0.0
pt:17   sig:    -0.1271         res:    -0.1271         var     0.0
pt:18   sig:    -0.1036         res:    -0.1036         var     0.0
pt:19   sig:    0.1546          res:    0.1546          var     0.0
pt:20   sig:    0.0415          res:    0.0415          var     0.0
pt:21   sig:    -0.6342         res:    -0.6342         var     0.0
pt:22   sig:    -1.3871         res:    -1.3871         var     0.0
pt:23   sig:    -1.4807         res:    -1.4807         var     0.0
pt:24   sig:    -0.6391         res:    -0.6391         var     0.0
pt:25   sig:    0.6391          res:    0.6391          var     0.0
pt:26   sig:    1.4807          res:    1.4807          var     0.0
pt:27   sig:    1.3871          res:    1.3871          var     0.0
pt:28   sig:    0.6342          res:    0.6342          var     0.0
pt:29   sig:    -0.0415         res:    -0.0415         var     0.0
pt:30   sig:    -0.1546         res:    -0.1546         var     0.0
pt:31   sig:    0.1036          res:    0.1036          var     0.0
pt:32   sig:    0.1271          res:    0.1271          var     0.0
pt:33   sig:    -0.4294         res:    -0.4294         var     0.0
pt:34   sig:    -1.2347         res:    -1.2347         var     0.0
pt:35   sig:    -1.5475         res:    -1.5475         var     0.0
pt:36   sig:    -0.9217         res:    -0.9217         var     0.0
pt:37   sig:    0.3271          res:    0.3271          var     0.0
pt:38   sig:    1.351           res:    1.351           var     0.0
pt:39   sig:    1.4958          res:    1.4958          var     0.0
pt:40   sig:    0.8452          res:    0.8452          var     0.0
pt:41   sig:    0.0831          res:    0.0831          var     0.0
pt:42   sig:    -0.1802         res:    -0.1802         var     0.0
pt:43   sig:    0.0364          res:    0.0364          var     0.0
pt:44   sig:    0.1726          res:    0.1726          var     0.0
pt:45   sig:    -0.2424         res:    -0.2424         var     0.0
pt:46   sig:    -1.0498         res:    -1.0498         var     0.0
pt:47   sig:    -1.5515         res:    -1.5515         var     0.0
pt:48   sig:    -1.1623         res:    -1.1623         var     0.0
pt:49   sig:    -0.0            res:    0.0             var     0.0

重构的信号与原始信号之间的方差为0，完美重构。

后记

尽管从理论上说，离散傅里叶是连续傅里叶的扩展形式，但实际上用的最多的还是离散傅里叶，甚至你可以不必理解什么是复平面，什么是连续傅里叶，什么是无穷级数。毕竟无论是python，还是C/C++，甚至其他工程语言，只要涉及数值计算，就一定有包含傅里叶分析的数学工具包可以使用，而且执行效率已经被优化的非常快。

这是否意味着入门者不再需要了解傅里叶怎么计算了吗？对此我有一些个人体会，当你遇到一些噪音特别大，有效信号很弱的场景时，你需要根据使用场景进行巧妙的设计参数才能比较理想的提取出你需要的信号部分。

如果单纯的设定滤波阈值，很可能在某些情况下可以正常使用，而其他场景下随缘了。事实上，使用傅里叶处理数据都是在假设数据是理想条件下输入，比如有较高的SNR比。但是实际工作中，这种情况往往难得，换句话说，真实环境实在过于Egg疼了，所以在很多情况下我并不会优先考虑傅里叶。

但是，这不妨碍傅里叶本人及其思想对于科学、工程界的重要贡献。事实上通过对傅里叶这一伟大思想的梳理，能学会更多，你说是吧？