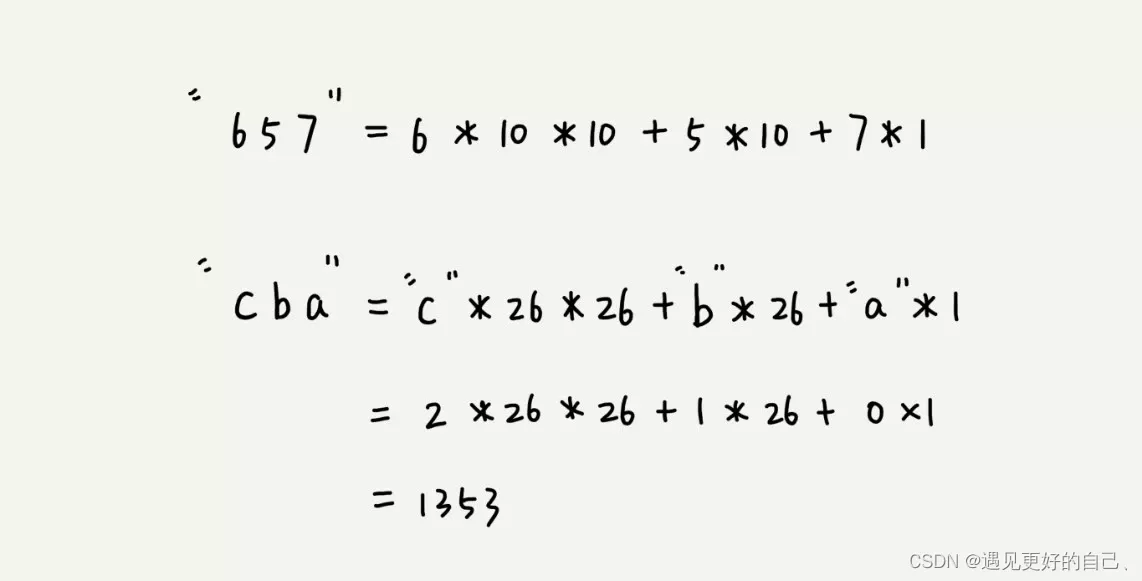---

字符串匹配

一、基本概念

字符串匹配问题

假设文本是一个长度为$n$的数组$T[1\dots n]$，而模式是一个长度为$m$的数组$P[1\dots m]$，其中$m\le n$，进一步假设$P$和$T$的元素都是来自一个有限的字母集$\sum$的字符。数组$T$和$P$通常被称为字符串。

如果$0\le s\le n-m$，并且$T[s+1\dots s+m]=P[1\dots m]$，那么称模式$P$在文本$T$中出现过，且偏移为$s$。如果$P$在$T$中以偏移$s$出现，那么称$s$为有效偏移，否则为无效偏移。

字符串匹配问题就是在$T$中找到$P$的所有有效偏移$s$。

符号和术语

1. 字符串集合：我们用${\sum }^{\ast }$来表示包含所有有限长度的字符串的集合，该字符串是由字母表$\sum$中的字符串组成。在本文中，我们只考虑有限长度的字符串。长度为$0$的字符串用$ϵ$表示，也属于${\sum }^{\ast }$。
2. 字符串的长度：一个字符串$T$的长度用$|T|$表示。特别的，$|ϵ|=0$。
3. 连结：两个字符串$x$和$y$的连结表示为$xy$，意义为$x$后接$y$，长度为$|x|+|y|$。
4. 前缀：如果对于三个个字符串$x=wy$，那么称字符串$w$是$x$的前缀，记作$w⊏x$，且$|w|\le |x|$。
5. 后缀：如果对于三个个字符串$x=yw$，那么称字符串$w$是$x$的后缀，记作$w⊐x$，且$|w|\le |x|$。特别的，空字符串$ϵ$是任意一个字符串的前缀和后缀。

后缀重叠引理

假设$x$，$y$和$z$满足$x⊐z$和$y⊐z$。如果$|x|\le |y|$，那么$x⊐y$，反过来如果$|y|\le |x|$，那么$y⊐x$。如果$|x|=|y|$，那么$x=y$。

为了符号简洁，我们把模式$P[1\dots m]$的由$k$个字符串组成的的前缀$P[1\dots k]$，记作$P_k$。因此$P_0=ϵ,P_m=P=P[1\dots m]$。与此类似，我们把文本$T$中由$k$个字符组成的前缀记作$T_k$。

字符串匹配问题转化为：找到所有的偏移$s(0\le s\le n-m)$，使得$P⊐T_{s+m}$。

---

二、朴素字符串匹配算法

朴素字符串算法是通过一个循环找到所有的有效偏移，该循环对$n-m+1$个可能的$s$值进行检测，看是否满足条件$P[1\dots m]=T[s+1\dots s+m]$。

NAIVE-STRING-MATCHER(T,P):n = T.lengthm = P.lengthfor s = 0 to n-m:if P[1...m] = T[s+1 ... s+m]:print "Pattern occurs whit shift",s

伪代码中的循环枚举$s$的位置，for中的判断隐含了一个循环，这个循环检测偏移$s$是否为有效偏移。

在最坏情况下，朴素算法的运行时间为$O((n-m+1)m)$。如果$m=n/2$，则运行时间为$\Theta (n^2)$。

我们看到，朴素字符串匹配算法不是解决该问题的最佳过程。是因为当其他无效的$s$值存在时，他只关心一个有效的$s$的值，而完全忽略了检测无效的$s$值的时候所带来的有用信息。例如对于$P=aaab$并且我们发现$s=0$是一个有效的偏移值，由于$T[4]=b$，所以$s=1,2,3$都不是有效的。

三、Rabin-Karp算法(字符串Hash算法)

进制Hash

Rabin-Karp算法运用了初等数论的知识，其实就是对字符串进行$Hash$运算，比较每一位上的$Hash$值是否相等即可。

为了便于说明，我们假设 ∑ = { 0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 } \sum = \{0,1,2,3,4,5,6,7,8,9\} ∑={0,1,2,3,4,5,6,7,8,9}，这样每个字符都是十进制数字。（在通常情况下，可以假定每个字符都是以$d$为基数表示的数字，其中$|\sum |=d$），每一个字符串就是相当与一个十进制数，其长度为$k$。

给定一个模式$P[1\dots m]$，令$p$为表示的十进制数。类似的，有字符串$T[1\dots n]$，假设$t_s$表示子串$T[s+1\dots s+m]$对应的十进制数。当然，只有当$s$是一个有效偏移的时候，$p=t_s$，如果能在时间$\Theta (m)$内计算出$p$的值，并且在总时间$\Theta (n-m+1)$内计算出所有的$t_s$值，那么通过比较$t_s$和$p$的值就可以在时间$\Theta (m)+\Theta (n-m+1)=\Theta (n)$时间内找到所有的有效偏移。

其实这是一种$Hash$运算，根据霍纳法则，我们可以在规定的时间内计算出$p$：

$$p=P[m]+10(P[m-1]+10(P[m-2]+\dots +10(P[2]+10P[1])\dots ))$$

类似的，我们可以通过规定的时间计算出$t_0$的值，并且能在$O(1)$的时间内利用$t_0$的值计算出$t_1$的值，依次类推，总结出递推公式：

$$t_{s+1}=10(t_s-10^{m-1}T[s+1])+T[s+m+1]$$

减去$10^{m-1}T[s+1]$，表示减去最高位的数字，乘以十表示将这个数向左移动一位，加上$T[s+m+1]$，表示加上最低位。

预先计算出常数$10^{m-1}$，可以使用快速幂计算。

到目前为止，我们就始终在回避一个问题，如果$m$的值过大，则$t_i$的值就可能很大，以至于超过了运算的范围，因此我们就需要运用数论的知识，将其进行取模运算。

选定一个素数$q$，使得$dq$在一个机器字长内，我们就可以进行取余运算：

$$t_{s+1}=(d(t_s-hT[s+1])+T[s+m+1])\mathrm{m}\mathrm{o}\mathrm{d}q$$

其中$d$为$d$进制，$h$为$h\equiv d^{m-1}\mathrm{m}\mathrm{o}\mathrm{d}q$。

但是这种结果并不是很完美，因为$t_s\equiv p\mathrm{m}\mathrm{o}\mathrm{d}q$，并不能说明$t_s=p$，因此，我们还必须仿照朴素算法那样，验证一下这个答案。

如果$q$是一个素数，并且这个$q$足够大，这种伪命中点的概率发生的几率很小。

Rabin-Karp算法的期望时间复杂度为$O(n)+O(m(v+n/q))$。预计较好的情况（有效偏移比较少，素数大，$m$远远小于$n$）。这个算法的时间复杂度为$O(n)$。

还可以使用链接法或开放寻址法来进行无错Hash。

同时，我们可以定义$h[0]=s[0]$，$h[k]=(h[k-1]A+s[k])\mathrm{m}\mathrm{o}\mathrm{d}B$，位权$p[0]=1$，$p[k]=(p[k-1]A)\mathrm{m}\mathrm{o}\mathrm{d}B$。

这样我们就能在$O(1)$的时间内计算出某个子串$S[a\dots b]$的hash值$(h[b]-h[a-1]p[b-a+1])\mathrm{m}\mathrm{o}\mathrm{d}B$。

质数Hash

如果我们想判断两个单词是不是同体词（即两个字符串每个字母出现的次数都相同，例如eat和ate）。此时我们将每一个字母替换成一个唯一的质数，那么根据算数基本定理，我们就可以把一个字符串看成是一个由多个质数相乘得到的唯一的整数，那么如果两个单词是同体词，那么这个两个Hash值一定相等。

四、利用有限自动机进行字符串匹配

有限自动机

一个有限自动机$M$是一个五元组$(Q,q_0,A,\sum ,\delta )$，其中：

• $Q$是状态的有限集合
• $q_0\in Q$是初始状态
• $A\subseteq Q$是一个特殊接受状态的集合
• $\sum$是有限输入字母表
• $\delta$是一个从$Q\times \sum$到$Q$的函数，称为$M$的转移函数

有限自动机状态开始于$q_0$，读入一个字符$a$，则他从状态$q$变成了状态$\delta (q,a)$。当自动机的状态属于$Q$的时候，我们说自动机接受了迄今为止所有的字符。

有限自动机$M$引入一个终态函数$\varphi (w)$，他是一个从${\sum }^{\ast }$到$Q$的一个函数，函数的值为自动机$M$处理完字符串$w$之后所处的最终状态。因此当且仅当$\varphi (w)\in A$的时候，$M$接受字符串$w$。存在递归定义：

$$\begin{gathered} \varphi (ϵ)=q_0 \\ \varphi (wa)=\delta (\varphi (w),a) \end{gathered}$$

字符串匹配自动机

对于给定一个模式$P$，我们可以进行预处理构造一个有限状态自动机，之后，对于字符串$T$，就可以在$O(n)$的时间内求出所有的有效偏移。

为了构造自动机，我们要先定义后缀函数$\sigma (x)$，函数是一个从${\sum }^{\ast }$到 { 0 , 1 , 2 , 3 , … , m } 的 映 射 函 数 \{0,1,2,3,\ldots,m\}的映射函数 {0,1,2,3,…,m}的映射函数：

给定模式$P$，模式$P$的后缀函数为

$$\sigma (x)=\max (k:P_k⊐x)$$

也就是说存在一个最大长度的子串，既是$P$的前缀又是$x$的后缀，子串的长度就是后缀函数的值。

给定模式$P[1\dots m]$对应的字符串匹配自动机为：

• 状态集合$Q$为 { 0 , 1 , 2 , 3 , … , m } \{0,1,2,3,\ldots,m\} {0,1,2,3,…,m}。开始状态$q_0$为$0$，并且只有状态$m$是唯一的接受状态。
• 对于任意的状态$q$和字符$a$，转移状态函数$\delta (q,a)$的定义为$\delta (q,a)=\sigma (P_{q}a)$

也就是说，存在有效偏移$s$，那么$P$一定是$T_{s+m}$的后缀，状态机的状态就是后缀函数的值。并且存在有效偏移$s$，当且仅当状态$q=m$。

状态机维护一个不变式：

$$\varphi (T_i)=\sigma (T_i)$$

$T_i$表示$T[1\dots i]$。

图片中描述了模式$P=ababaca$的自动机的$DAG$模型，除了这个模型，还有二维表模型。

考虑一下两种情况：

• $a=P[q+1]$，此时我们可以放心的把状态转移到$\sigma (P_{q}a)=q+1$，这个状态沿着主轴的方向进行。
• $a\ne P[q+1]$，这时我们必须找到一个更小的子串，确保这个子串满足$\sigma (P_{q}a)$

此时，构造完自动机，我们就可以根据自动机处理文本$T$，找到状态$q=m$的时候，偏移$i-m$就是有效偏移。

为了证明有限自动机的正确性，我们首先要说明两个引理。

后缀不等式：对于任意字符串$x$和字符$a$，$\sigma (xa)\le \sigma (x)+1$。

也就是说如果字符$a$正好是下一个字符，等号成立，如果不是，那么后缀不可能再长了。

后缀函数递归定理：对任意字符串$x$和字符$a$，若$q=\sigma (x)$，则$\sigma (xa)=\sigma (P_{q}a)$。

也就是说，$P_q$这个后缀已经到了左边界，即从左边界开始求即可。

定理：如果$\varphi$是有限自动机的终态函数，那么$\varphi (T_i)=\sigma (T_i)$。

证明对$i$进行归纳即可。

计算状态转移函数

先确定一个$k$的上界，然后在缩小范围即可，这种方式效率很低，接下来的$KMP$算法可以优化这个思路。

代码

int sp[100][10];int eval(const string & p)
{for(int q = 0; q<=p.size(); q++){for(char a = '0'; a<='9'; a++){int k = q + 1;string x = p.substr(0,q) + a;while(1){bool ok = true;for(int i = x.size() - 1,j=k-1; j>=0; i--,j--){if(p[j] != x[i]){ok = false;break;}}if(ok) break;else k--;}sp[q][a] = k;}}
}void match(const string & t,int end)
{int q = 0;for(int i = 0; i<t.size(); i++){q = sp[q][t[i]];if(q == end) cout << i - end + 1 << endl;}
}int main()
{string p = "01011";string t = "0101111010111010101011111";int end = p.size();eval(p);match(t,end);return 0;
}

五、Knuth-Morris-Pratt算法

现在来介绍一种线性的字符串匹配算法$KMP$算法。和自动机算法相比，他只需要用到一个辅助函数$\pi$，而且这个函数和字符集无关，不需要遍历字符集。并且在$O(m)$的时间计算出所有的函数值以留备用，在$O(n)$的时间内完成匹配。

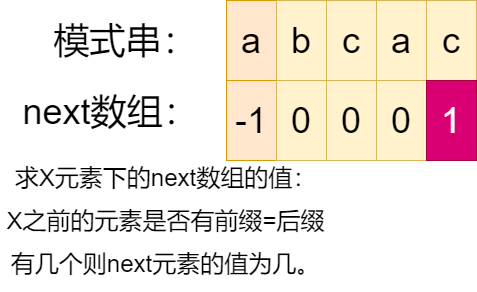
模式的前缀函数

面对一个偏移$s$，匹配长度为$q$，字符$q+1$匹配失败，按照朴素算法，我们应该测试下一个偏移$s+1$，但是我们知道，偏移$s+1$必然失败，因为$P[1]$必然不可能匹配$T[s+2]$，可以匹配的最短偏移为$s+2$。这个$2$我们可以通过计算前缀函数计算出来。

也就是说，假设模式字符串$P[1\dots q]$与文本字符串$T[s+1\dots s+q]$匹配，$s^{\prime }$是最小的偏移量，$s^{\prime }>s$，那么对某些$k<q$满足：

$$P[1\dots k]=T[s^{\prime }+1\dots s^{\prime }+k]$$

的最小偏移$s^{\prime }$是多少，其中$s^{\prime }+k=s+q$。

这时，我们就需要借助前缀函数$\pi (q)$，其值为存在最长的子串，既是$P$的前缀，又是$P_q$的真后缀。

已知一个模式$P[1\dots m]$，模式$P$的前缀函数是函数 π : { 1 , 2 , 3 , 4 , … , m } → { 0 , 1 , … , m − 1 } \pi: \{1,2,3,4,\ldots,m\} \to \{0,1,\ldots,m-1\} π:{1,2,3,4,…,m}→{0,1,…,m−1}的一个函数，满足：

$$\pi [q]=max(k:k<q|P_k⊐P_q)$$

之后我们就可以利用辅助函数匹配文本。

代码

#include <bits/stdc++.h>using namespace std;#define FR freopen("in.txt", "r", stdin)typedef long long ll;int nxt[1000005];void buildNext(string &p)
{nxt[0] = 0;for (int i = 1; i < p.size(); i++){nxt[i] = nxt[i - 1];while (p[nxt[i]] != p[i] && nxt[i] > 0){nxt[i] = nxt[nxt[i] - 1];}nxt[i] = p[nxt[i]] == p[i] ? nxt[i] + 1 : 0;}
}void kmp(string &t, string &p)
{int ti = 0;int pi = 0;while (ti < t.size()){if (t[ti] == p[pi]){if (pi == p.size() - 1){cout << ti + 2 - p.size() << endl;pi = nxt[pi];}else{pi++;}ti++;}else if (pi == 0){ti++;}else{pi = nxt[pi - 1];}}
}int main()
{string s1, s2;cin >> s1 >> s2;buildNext(s2);kmp(s1, s2);for (int i = 0; i < s2.size(); i++){cout << nxt[i] << " ";}return 0;
}

六、Z-函数（扩展KMP）

定义$Z$数组$Z[i]$为，字符串$s[0\dots i-1]$和字符串$s[i\dots n-1]$的最长公共前缀长度。特别的$Z[0]=0$。

我们有线性时间$O(n)$的算法来计算Z-函数，叫做Z-算法。