1. 概述
维特比算法是安德鲁.维特比(Andrew Viterbi)于1967年为解决通信领域中的解码问题而提出的,它同样广泛用于解决自然语言处理中的解码问题,隐马尔可夫模型的解码是其中典型的代表。无论是通信中的解码问题还是自然语言处理中的解码问题,本质上都是要在一个篱笆网络中寻找得到一条最优路径。
所谓篱笆网络,指的是单向无环图,呈层级连接,各层节点数可以不同。如图是一个篱笆网络,连线上的数字是节点间概念上的距离(如间距、代价、概率等),现要找到一条从起始点到终点的最优路径。
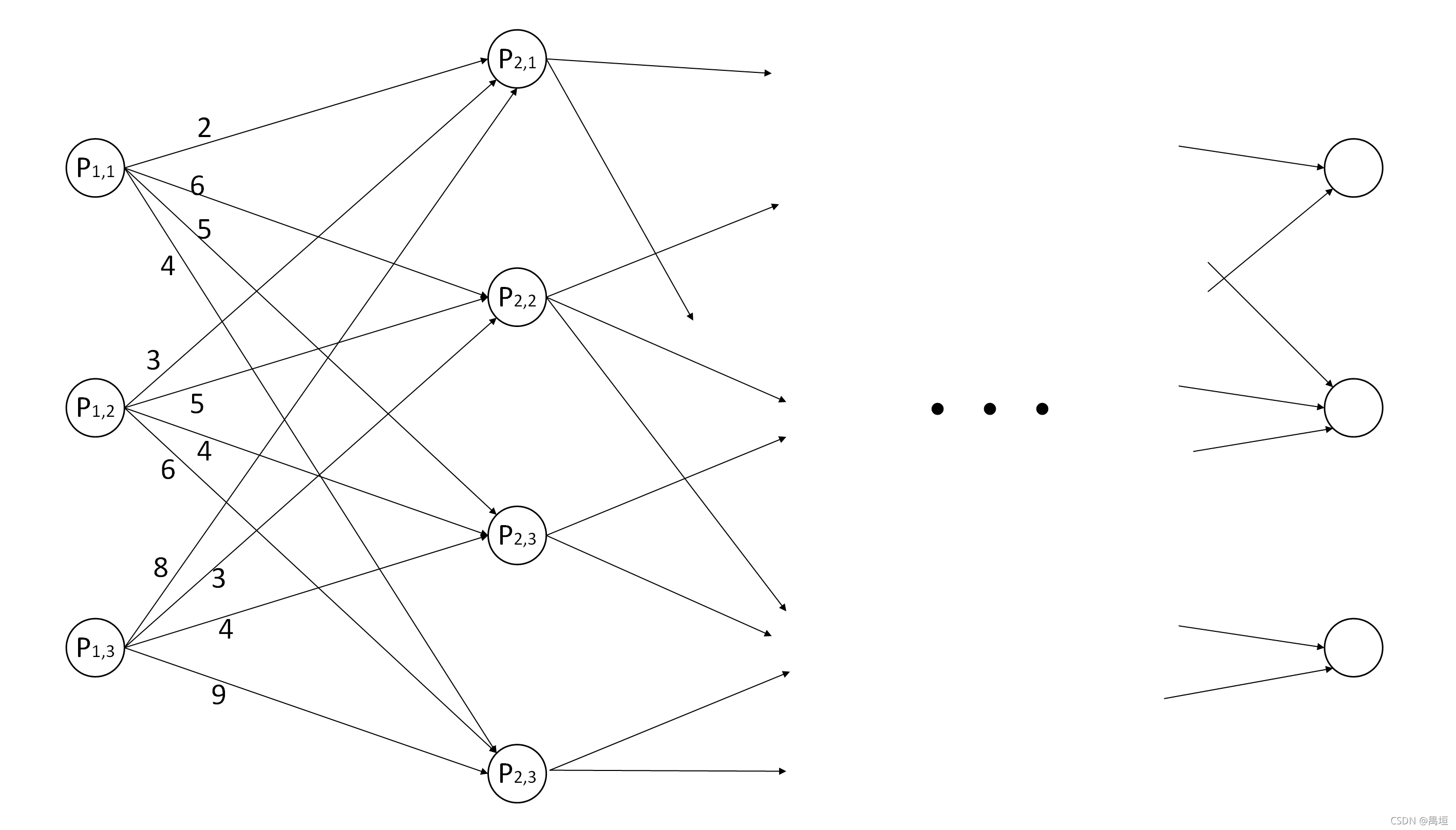
在实际问题中,节点数和层数往往是大量的,因而采取遍历所有的路径计算其距离进行比较的方式是不可行的。维特比算法正是通过动态规划的方式高效求得这条最优路径。
2.算法原理
该问题具有这样一个特性,对于最优(如最短距离)的路径,任意一段子路径一定是该段两端点间所有可达路径中最优的,如若不然,将该段中更优的子路径接到两端点便构成了另一个整体最优路径,这是矛盾的。或者说,最优路径中,从起始点到由近及远的任一点的子路径,一定是该段所有可达路径中最优的。也即,整体最优,局部一定最优。

该特性也就是说,对每个节点而言,如果最优路径经过这一点,则一定是经过从起始点到这点的这段最优路径。那么,只要从头开始,由局部向整体推进,渐次地找到起始点到当前点的最优路径,算至终点便得到了整体最优路径。这样的方式叫做动态规划,是维特比算法的基本思想。
维特比算法求解篱笆网络最短路径的过程为:
从第一层开始,对每一层的每一个节点,计算出起始点到它的最短距离,并记录下相应最短路径下它的前一个节点,逐层递推,算至终止点时便得到了整体最短距离,再依照节点记录下的前置节点进行回溯,就得到了最短路径的序列。对第 i i i层第 j j j个节点 P i , j P_{i,j} Pi,j,假设起始点到它的最短距离为 D ( P i , j ) D\left( P_{i,j} \right) D(Pi,j),相应最短路径下它的前一个节点为 P r e ( P i , j ) Pre\left( P_{i,j} \right) Pre(Pi,j),则
D ( P i , j ) = min 1 ≤ k ≤ N [ D i − 1 , k + d ( P i − 1 , k , P i , j ) ] D\left( P_{i,j} \right)=\min_{1\leq k \leq N}{\left[ D_{i-1,k}+d(P_{i-1,k},P_{i,j}) \right]} D(Pi,j)=1≤k≤Nmin[Di−1,k+d(Pi−1,k,Pi,j)]
也就是,对前一层的所有节点,计算每一个节点的记录的最短距离D与它到当前节点的距离d的和,取其中最小的那个值(其中, d ( A , B ) d(A,B) d(A,B)表示A,B两节点间的距离。).
P r e ( P i , j ) = P i − 1 , j ∗ = a r g min 1 ≤ k ≤ N [ D i − 1 , k + d ( P i − 1 , k , P i , j ) ] Pre\left( P_{i,j} \right)=P_{i-1,j\ast}=arg\min_{1\leq k \leq N}{\left[ D_{i-1,k}+d(P_{i-1,k},P_{i,j}) \right]} Pre(Pi,j)=Pi−1,j∗=arg1≤k≤Nmin[Di−1,k+d(Pi−1,k,Pi,j)]
也就是,满足距离最短的那条路径上在前一层的节点.
3.示例
在如下网络中,连线上的数字是节点间的距离,求S点到E点的最短距离和与之对应的路径。
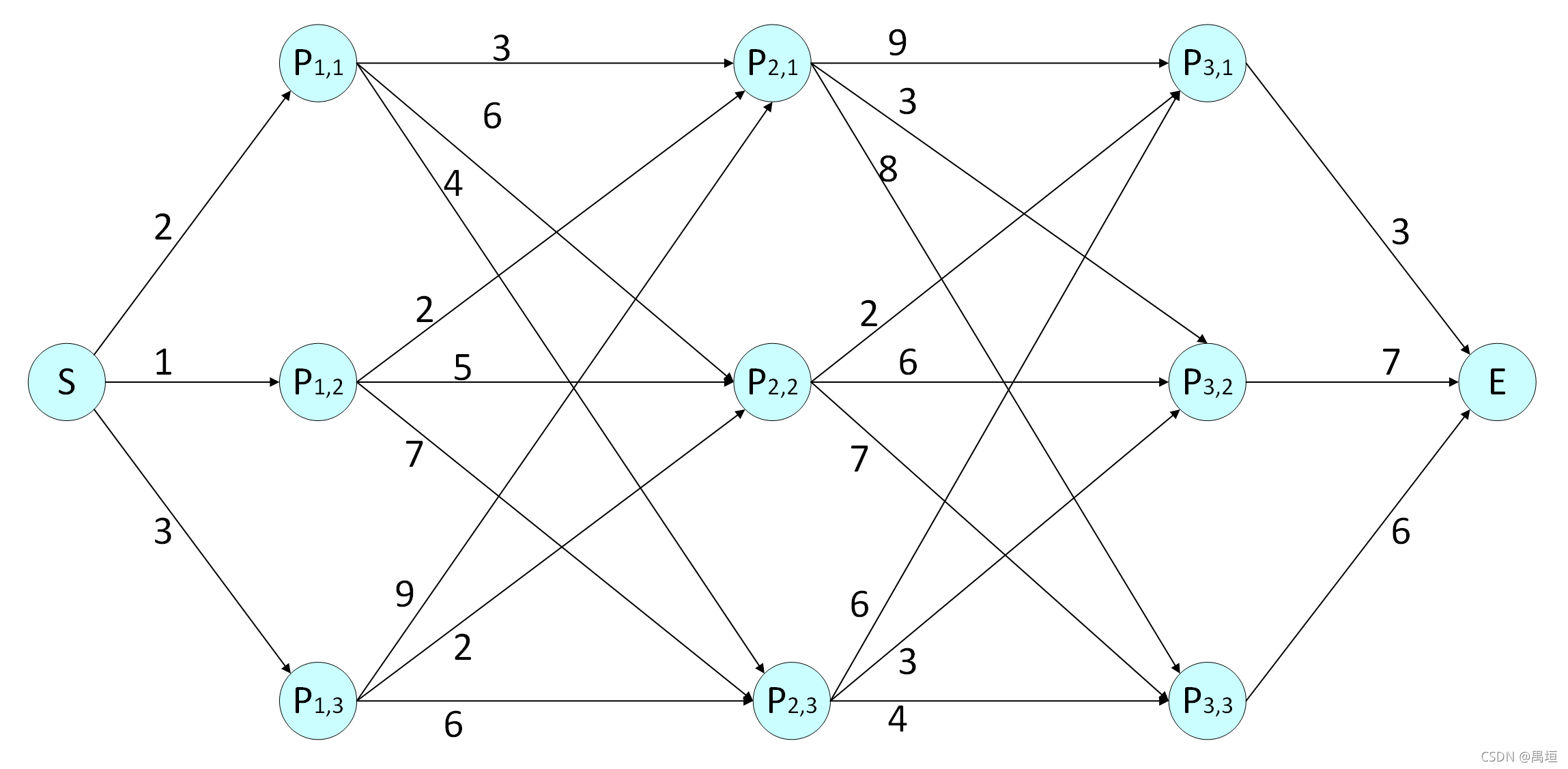
第一层:
对节点 P 1 , 1 P_{1,1} P1,1,
起始点到它只有一条路径,最短距离 D ( P 1 , 1 ) = 2 D(P_{1,1})=2 D(P1,1)=2,前一个节点 P r e ( P 1 , 1 ) = S Pre(P_{1,1}) = S Pre(P1,1)=S;
对节点 P 1 , 2 P_{1,2} P1,2,
起始点到它只有一条路径,最短距离 D ( P 1 , 2 ) = 1 D(P_{1,2}) = 1 D(P1,2)=1,前一个节点 P r e ( P 1 , 2 ) = S Pre(P_{1,2}) = S Pre(P1,2)=S;
对节点 P 1 , 3 P_{1,3} P1,3,
起始点到它只有一条路径,最短距离 D ( P 1 , 3 ) = 3 D(P_{1,3}) = 3 D(P1,3)=3,前一个节点 P r e ( P 1 , 3 ) = S Pre(P_{1,3}) = S Pre(P1,3)=S 。
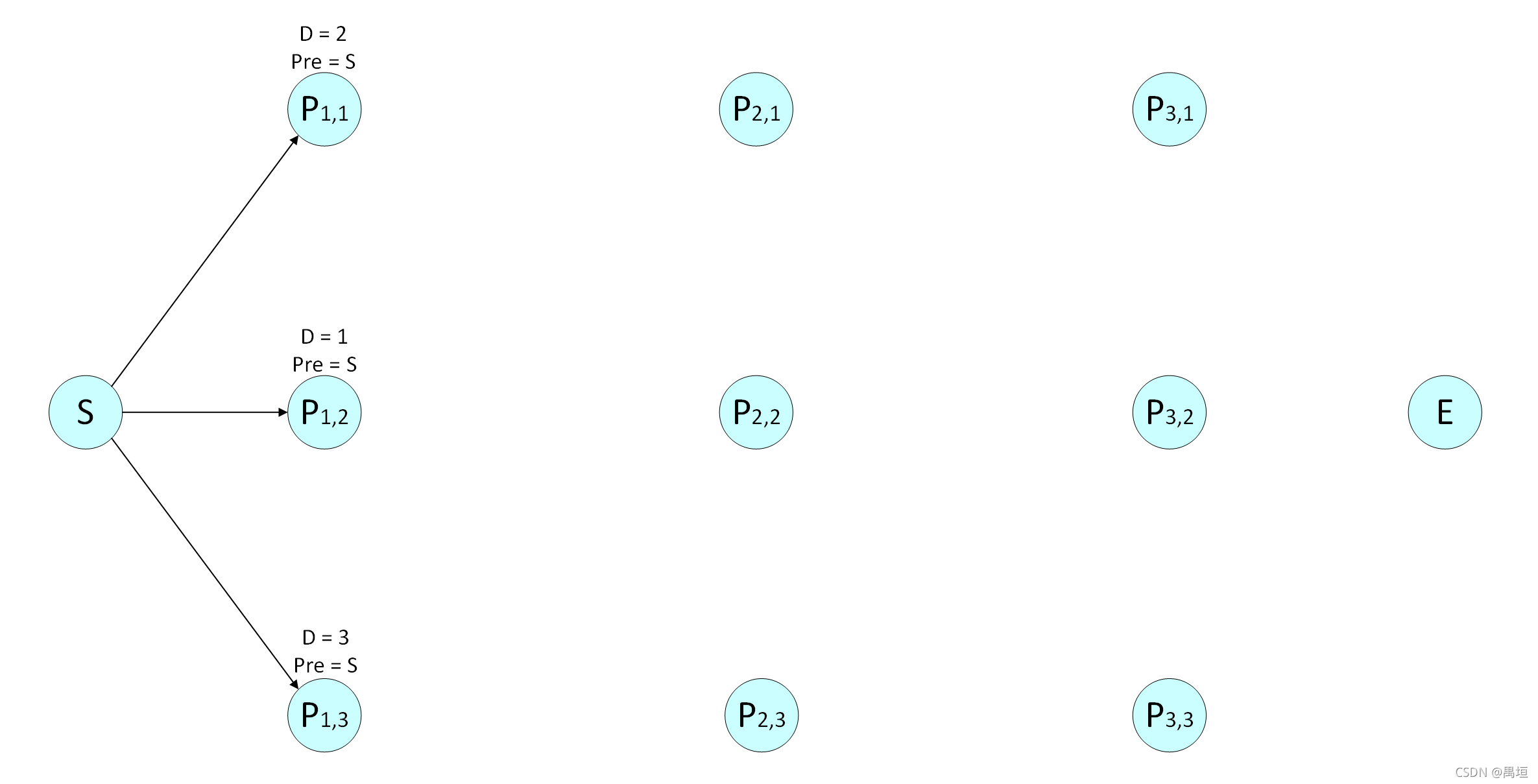
第二层:
对节点 P 2 , 1 P_{2,1} P2,1,
D ( P 1 , 1 ) + d ( P 1 , 1 , P 2 , 1 ) = 2 + 3 = 5 D(P_{1,1}) + d(P_{1,1},P_{2,1}) = 2 + 3 = 5 D(P1,1)+d(P1,1,P2,1)=2+3=5,
D ( P 1 , 2 ) + d ( P 1 , 2 , P 2 , 1 ) = 1 + 2 = 3 D(P_{1,2}) + d(P_{1,2},P_{2,1}) = 1 + 2 = 3 D(P1,2)+d(P1,2,P2,1)=1+2=3 ,
D ( P 1 , 3 ) + d ( P 1 , 3 , P 2 , 1 ) = 3 + 9 = 12 D(P_{1,3}) + d(P_{1,3},P_{2,1}) = 3 + 9 = 12 D(P1,3)+d(P1,3,P2,1)=3+9=12,
最短距离 D ( P 2 , 1 ) = m i n { 5 , 3 , 12 } = 3 D(P_{2,1}) = min\left\{ 5,3,12 \right\} = 3 D(P2,1)=min{5,3,12}=3,前一个节点 P r e ( P 2 , 1 ) = P 1 , 2 Pre(P_{2,1}) = P_{1,2} Pre(P2,1)=P1,2 ;
对节点 P 2 , 2 P_{2,2} P2,2 ,
D ( P 1 , 1 ) + d ( P 1 , 1 , P 2 , 2 ) = 2 + 6 = 8 D(P_{1,1}) + d(P_{1,1},P_{2,2}) = 2 + 6 = 8 D(P1,1)+d(P1,1,P2,2)=2+6=8,
D ( P 1 , 2 ) + d ( P 1 , 2 , P 2 , 2 ) = 1 + 5 = 6 D(P_{1,2}) + d(P_{1,2},P_{2,2}) = 1 + 5 = 6 D(P1,2)+d(P1,2,P2,2)=1+5=6,
D ( P 1 , 3 ) + d ( P 1 , 3 , P 2 , 2 ) = 3 + 2 = 5 D(P_{1,3}) + d(P_{1,3},P_{2,2}) = 3 + 2 = 5 D(P1,3)+d(P1,3,P2,2)=3+2=5,
最短距离 D ( P 2 , 2 ) = m i n { 8 , 6 , 5 } = 5 D(P_{2,2}) = min\left\{ 8,6,5 \right\} = 5 D(P2,2)=min{8,6,5}=5,前一个节点 P r e ( P 2 , 2 ) = P 1 , 3 Pre(P_{2,2}) = P_{1,3} Pre(P2,2)=P1,3 ;
对节点 P 2 , 3 P_{2,3} P2,3,
D ( P 1 , 1 ) + d ( P 1 , 1 , P 2 , 3 ) = 2 + 4 = 6 D(P_{1,1}) + d(P_{1,1},P_{2,3}) = 2 + 4 = 6 D(P1,1)+d(P1,1,P2,3)=2+4=6 ,
D ( P 1 , 2 ) + d ( P 1 , 2 , P 2 , 3 ) = 1 + 7 = 8 D(P_{1,2}) + d(P_{1,2},P_{2,3}) = 1 + 7 = 8 D(P1,2)+d(P1,2,P2,3)=1+7=8,
D ( P 1 , 3 ) + d ( P 1 , 3 , P 2 , 3 ) = 3 + 6 = 9 D(P_{1,3}) + d(P_{1,3},P_{2,3}) = 3 + 6 = 9 D(P1,3)+d(P1,3,P2,3)=3+6=9 ,
最短距离 D ( P 2 , 3 ) = m i n { 6 , 8 , 9 } = 6 D(P_{2,3}) = min\left\{ 6,8,9 \right\} = 6 D(P2,3)=min{6,8,9}=6,前一个节点 P r e ( P 2 , 3 ) = P 1 , 1 Pre(P_{2,3}) = P_{1,1} Pre(P2,3)=P1,1 ;
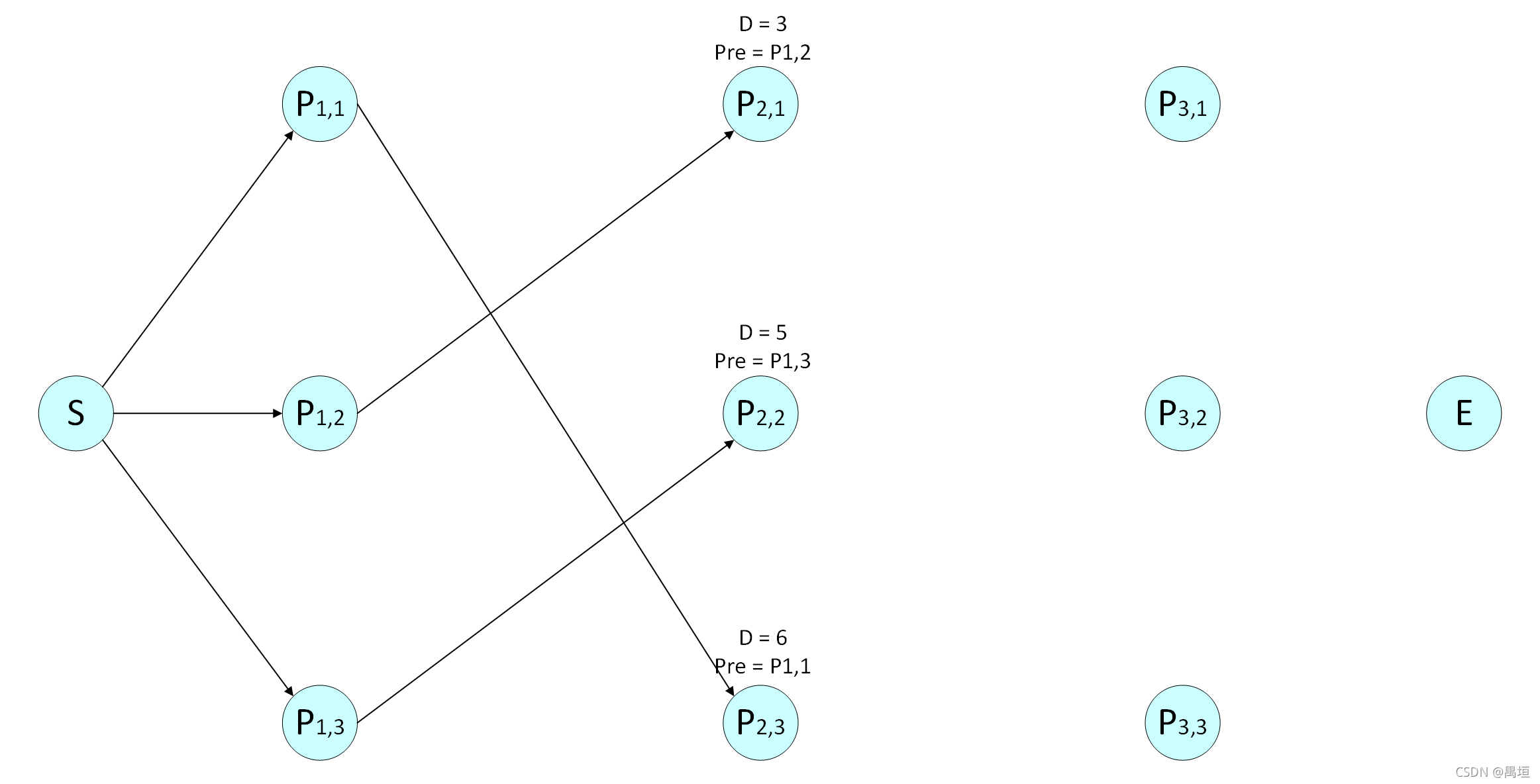
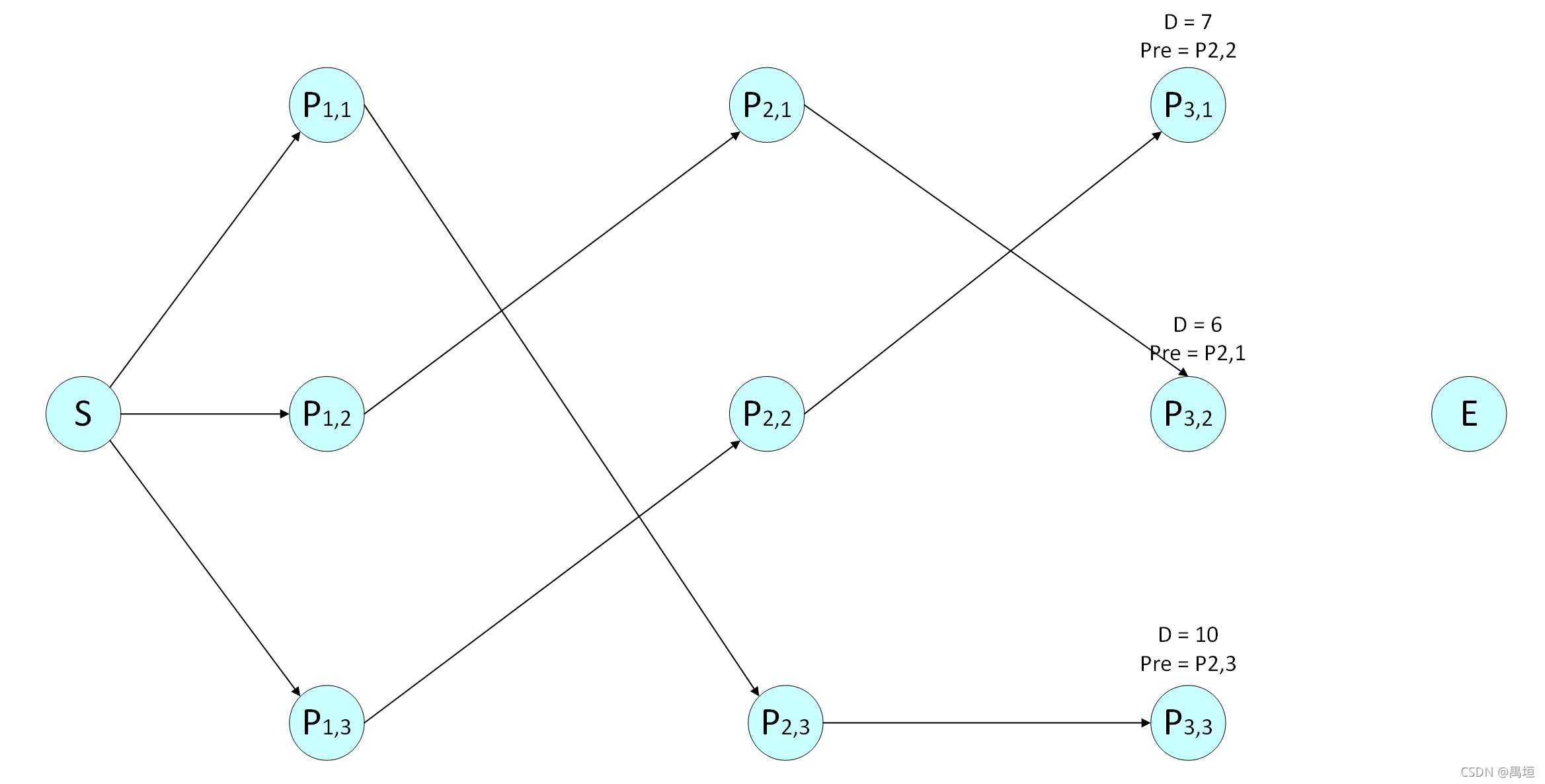
第三层:
对节点 P 3 , 1 P_{3,1} P3,1,
D ( P 2 , 1 ) + d ( P 2 , 1 , P 3 , 1 ) = 3 + 9 = 12 D(P_{2,1}) + d(P_{2,1},P_{3,1}) = 3 + 9 = 12 D(P2,1)+d(P2,1,P3,1)=3+9=12,
D ( P 2 , 2 ) + d ( P 2 , 2 , P 3 , 1 ) = 5 + 2 = 7 D(P_{2,2}) + d(P_{2,2},P_{3,1}) = 5 + 2 = 7 D(P2,2)+d(P2,2,P3,1)=5+2=7,
D ( P 2 , 3 ) + d ( P 2 , 3 , P 3 , 1 ) = 6 + 6 = 12 D(P_{2,3}) + d(P_{2,3},P_{3,1}) = 6 + 6 = 12 D(P2,3)+d(P2,3,P3,1)=6+6=12,
最短距离 D ( P 3 , 1 ) = m i n { 12 , 7 , 12 } = 7 D(P_{3,1}) = min\left\{ 12,7,12 \right\} = 7 D(P3,1)=min{12,7,12}=7,前一个节点 P r e ( P 3 , 1 ) = P 2 , 2 Pre(P_{3,1}) = P_{2,2} Pre(P3,1)=P2,2;
对节点 P 3 , 2 P_{3,2} P3,2,
D ( P 2 , 1 ) + d ( P 2 , 1 , P 3 , 2 ) = 3 + 3 = 6 D(P_{2,1}) + d(P_{2,1},P_{3,2}) = 3 + 3 = 6 D(P2,1)+d(P2,1,P3,2)=3+3=6,
D ( P 2 , 2 ) + d ( P 2 , 2 , P 3 , 2 ) = 5 + 6 = 11 D(P_{2,2}) + d(P_{2,2},P_{3,2}) = 5 + 6 = 11 D(P2,2)+d(P2,2,P3,2)=5+6=11,
D ( P 2 , 3 ) + d ( P 2 , 3 , P 3 , 2 ) = 6 + 3 = 9 D(P_{2,3}) + d(P_{2,3},P_{3,2}) = 6 + 3 = 9 D(P2,3)+d(P2,3,P3,2)=6+3=9,
最短距离 D ( P 3 , 2 ) = m i n { 6 , 11 , 9 } = 6 D(P_{3,2}) = min\left\{ 6,11,9 \right\} = 6 D(P3,2)=min{6,11,9}=6,前一个节点 P r e ( P 3 , 2 ) = P 2 , 1 Pre(P_{3,2}) = P_{2,1} Pre(P3,2)=P2,1;
对节点 P 3 , 3 P_{3,3} P3,3,
D ( P 2 , 1 ) + d ( P 2 , 1 , P 3 , 3 ) = 3 + 8 = 11 D(P_{2,1}) + d(P_{2,1},P_{3,3}) = 3 + 8 = 11 D(P2,1)+d(P2,1,P3,3)=3+8=11,
D ( P 2 , 2 ) + d ( P 2 , 2 , P 3 , 3 ) = 5 + 7 = 12 D(P_{2,2}) + d(P_{2,2},P_{3,3}) = 5 + 7 = 12 D(P2,2)+d(P2,2,P3,3)=5+7=12,
D ( P 2 , 3 ) + d ( P 2 , 3 , P 3 , 3 ) = 6 + 4 = 10 D(P_{2,3}) + d(P_{2,3},P_{3,3}) = 6 + 4 = 10 D(P2,3)+d(P2,3,P3,3)=6+4=10,
最短距离 D ( P 3 , 3 ) = m i n { 11 , 12 , 10 } = 10 D(P_{3,3}) = min\left\{ 11,12,10 \right\} = 10 D(P3,3)=min{11,12,10}=10,前一个节点 P r e ( P 3 , 3 ) = P 2 , 3 Pre(P_{3,3}) = P_{2,3} Pre(P3,3)=P2,3;
第四层(终点):
对节点 E E E,
D ( P 3 , 1 ) + d ( P 3 , 1 , E ) = 7 + 3 = 10 D(P_{3,1}) + d(P_{3,1},E) = 7 + 3 = 10 D(P3,1)+d(P3,1,E)=7+3=10,
D ( P 3 , 2 ) + d ( P 3 , 2 , E ) = 6 + 7 = 13 D(P_{3,2}) + d(P_{3,2},E) = 6 + 7 = 13 D(P3,2)+d(P3,2,E)=6+7=13,
D ( P 3 , 3 ) + d ( P 3 , 3 , E ) = 10 + 6 = 16 D(P_{3,3}) + d(P_{3,3},E) = 10 + 6 = 16 D(P3,3)+d(P3,3,E)=10+6=16,
最短距离 D ( E ) = m i n { 10 , 13 , 16 } = 10 D(E) = min\left\{ 10,13,16 \right\} = 10 D(E)=min{10,13,16}=10,前一个节点 P r e ( E ) = P 3 , 1 Pre(E) = P_{3,1} Pre(E)=P3,1;
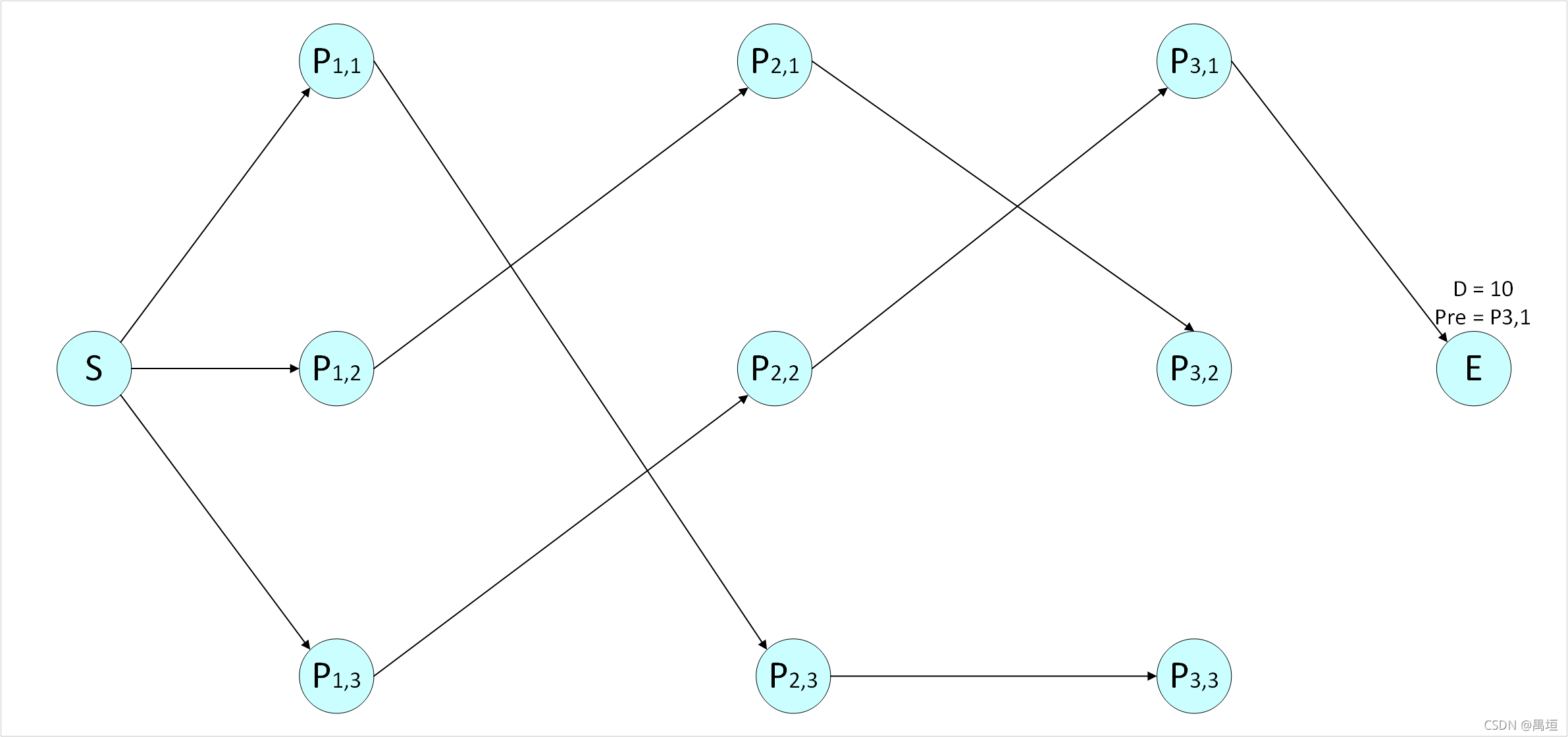
又 P r e ( E ) = P 3 , 1 Pre(E) = P_{3,1} Pre(E)=P3,1, P r e ( P 3 , 1 ) = P 2 , 2 Pre(P_{3,1}) = P_{2,2} Pre(P3,1)=P2,2, P r e ( P 2 , 2 ) = P 1 , 3 Pre(P_{2,2}) = P_{1,3} Pre(P2,2)=P1,3, P r e ( P 1 , 3 ) = S Pre(P_{1,3}) = S Pre(P1,3)=S
故最短距离为10,与之对应的路径为( S S S, P 1 , 3 P_{1,3} P1,3, P 2 , 2 P_{2,2} P2,2, P 3 , 1 P_{3,1} P3,1, E E E).
End.
参考
- 吴军. 数学之美(第二版). 人民邮电出版社.
- 李航. 统计学习方法. 清华大学出版社.