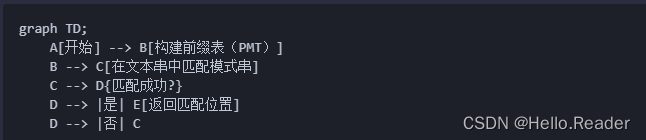
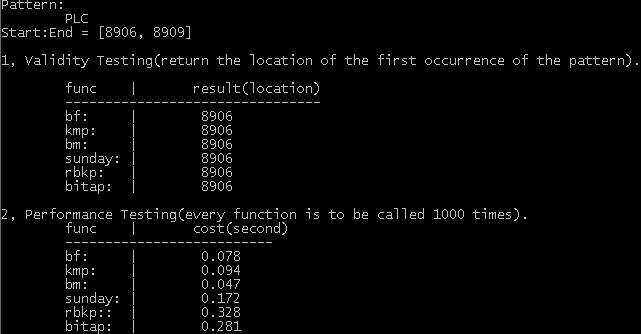
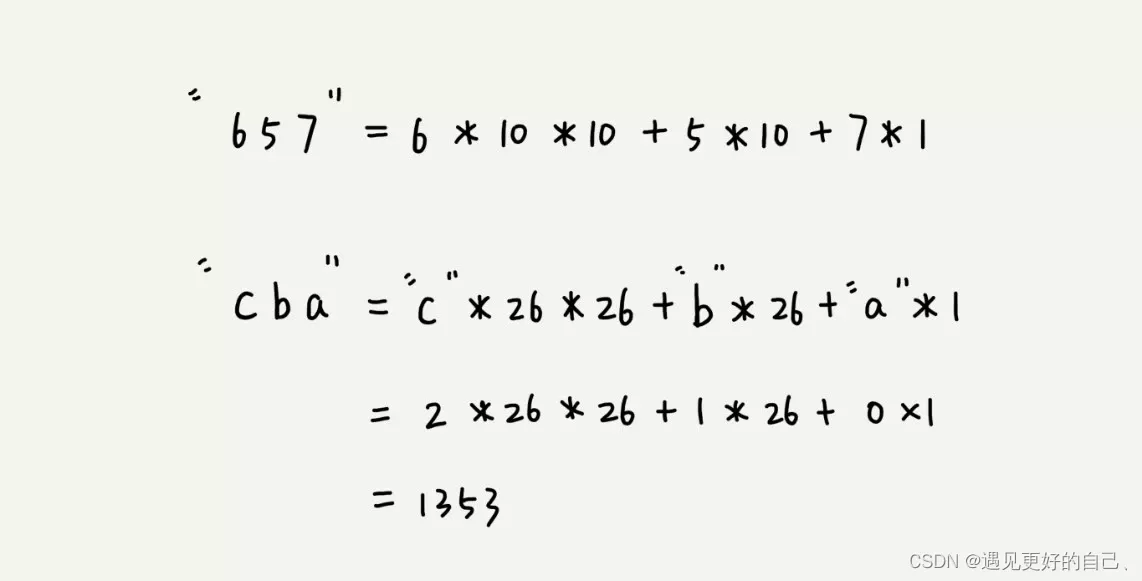小白给小白详解维特比算法（一）

---

初见HMM求解状态序列用到的维特比算法时，其实内心真的是崩溃的：数不尽的假设和公式，让人头昏脑涨的同时也击溃了自信心。但是仔细研究一下会发现其实问题蛮简单的，本文就致力于尝试用更通俗的方式解释一下维特比算法和它是如何运用在HMM求解状态序列中的，因为我也是刚看个差不多……所以如果有不对的地方请各位直接喷别留情！
（以下部分内容参考了吴军《数学之美》26.1，感谢吴军博士通俗易懂的讲解）

篱笆网络（Lattice）的最短路径问题

这个问题长什么样子？

尝试着回答一下这个问题（就算没办法回答也请先别关闭这个窗口！）：
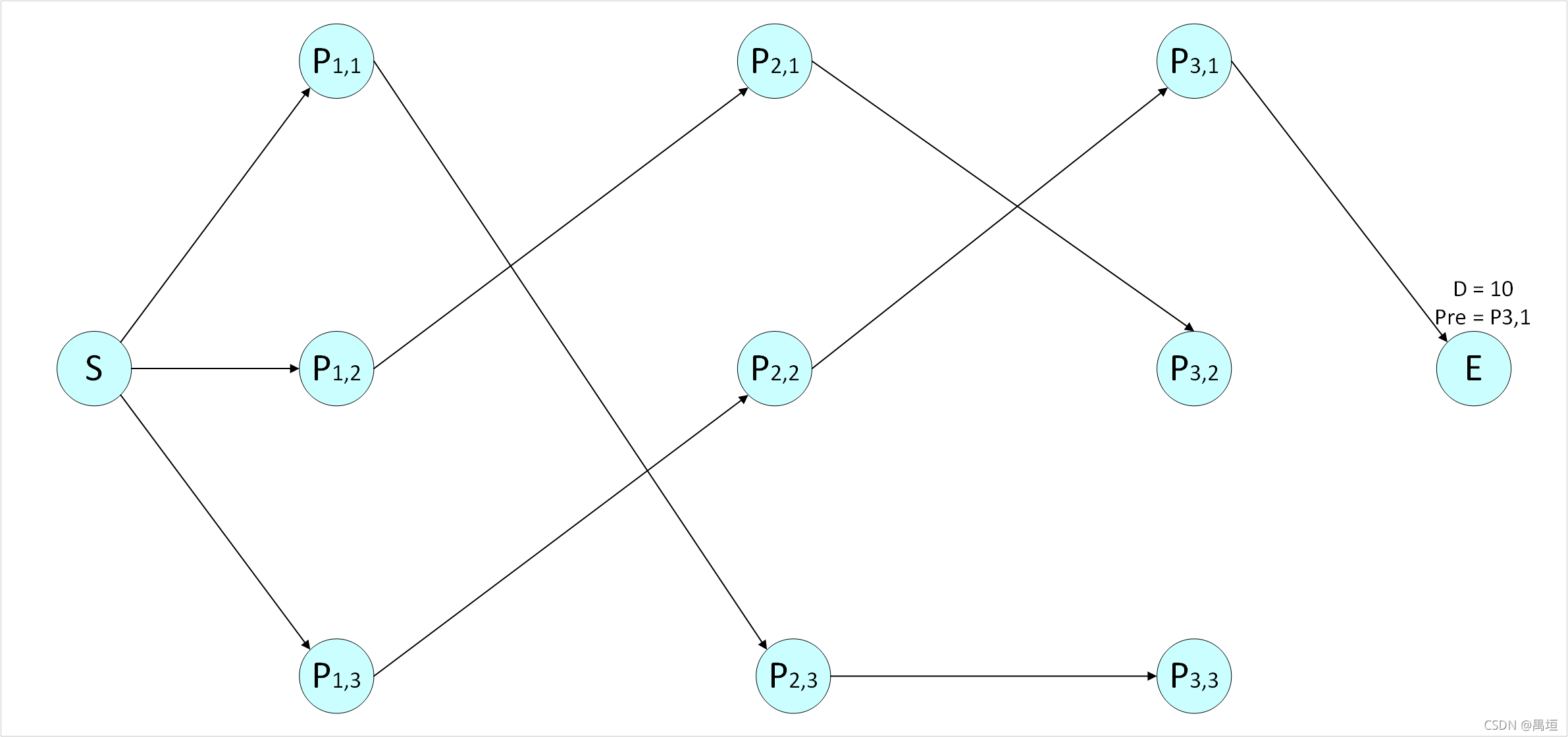
已知下图的篱笆网络，每个节点之间的数字表示相邻节点之间的距离，举个例子来说，如果我走$A\rightarrow B_1 \rightarrow C_2 \rightarrow D_1 \rightarrow E$，这个距离是$6+6+5+4=21$。那么如果让你从A走到E，最短路径是哪一条呢？

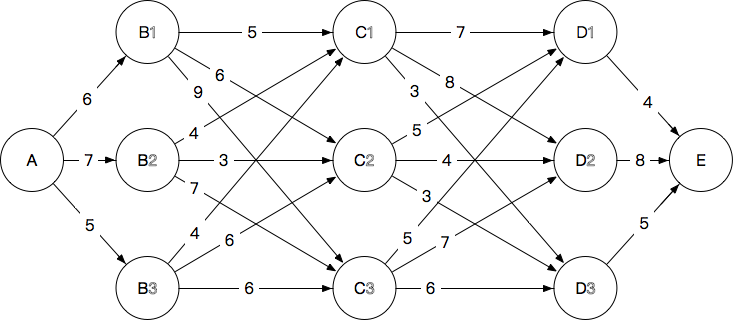
图1

这个问题难在哪里？

好啦不用尝试啦！显然大家都知道，通过穷举的方法是很容易得到最短路径，可是问题就在于如果穷举的话，需要的加法次数不用算你也知道实在是太多啦（每条路径需要计算$4$次加法，一共$3\times 3 \times 3=27$条路径共$108$次计算）！像这种没几层的篱笆网络也就罢了，如果每层13个节点，一共12层（然而这个规模对于标注问题来说也依然根本不算什么），可想而知那个线有多乱，如果仅仅穷举的话，这个计算量（大致是每条$12$次计算，一共$13^{12}$条路径共大约$12\times 13^{12}\approx 2\times 10^{15}$次计算）怕是超级计算机也吃不消。

为了不直接给公式让大家关掉窗口，我们尝试着一点一点来解决这个问题

简化成这个模样，你总能回答了吧？

如下图，如果我想让你找到$A\rightarrow E$的最短路径，就很简单了吧？

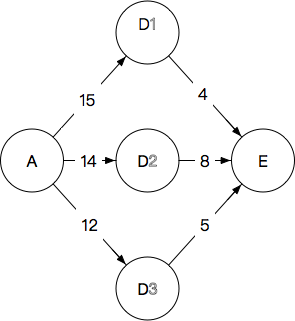
图2

显然图2上只有三条路径，我们分别计算之后得到最短路径应该是$A \rightarrow D_3 \rightarrow E$这一条，路程是17。

这个时候请把这个问题和上一个问题做一个对比，同时从相反的方向考虑一下上一个问题：如果我最终想要到达E这个节点，其实无论如何都是要经过D这一层的，那么要是我知道从A到D的每一个节点的最短路径长度（在刚才的图上，我们事实上假设了他们分别是15、14和12），再加上从D的各节点到E的路程就得到了最终路径的长度。

当然我们还需要再多想一点：如果想要真的按照A到E的最短路径来走的话，我们其实不会选择$D_1$和$D_2$这两个节点，因为哪怕（以）$A\rightarrow D_2$（为例）路径更短（就算是10），但是加上$D_2\rightarrow E$的距离之后就变得更长了（这时候也是18）。相应的我们也就明白这样一个道理：虽然我们最后没有选择$D_1$和$D_2$这两个节点，但我们是否真的就不需要得到A到他们的最短路径了呢？答案当然是否定的：从刚才的例子我们很容易理解，站在D层的角度来看的话，最终的长度是由“历史”（A到每一个D的长度）和“未来”（每一个D到E的长度）同时决定的，只有同时掌握了“历史”和“未来”，世界才能在我们手中（旁白：你说什么呢）！

当然刚才我们从A到D层的路径是假设出来的，事实上如果我们真的要解决最开始那个问题，我们需要求解这个问题：

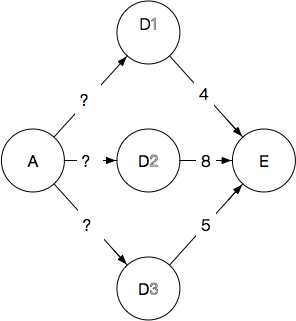
图3

我们就可以知道，最终的最短路径到底走的是哪个D。

下一步我们该干什么？

我们已经明白了，为了确定从哪个D到E才是最短的，我们就必须确定A到每一个D的最短路径。诶？这个问题是不是从哪里见过？

其实这就是所谓的“动态规划”的核心了：子问题几乎是完全一样的，我们只要一个一个解决了子问题（的子问题），最终的问题就迎刃而解了。

为了确定这个问题，我们就需要一个D一个D地去考虑（旁白：？？？），比如在考虑$D_1$的时候不考虑$D_2 、D_3、E$等等。把问题简化成这个样子：

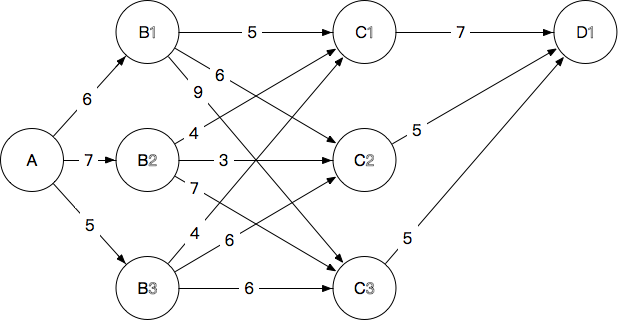
图4

这个图是不是和图1 非常相似？

然后根据图3的思想，我们把它简化成这个样子：

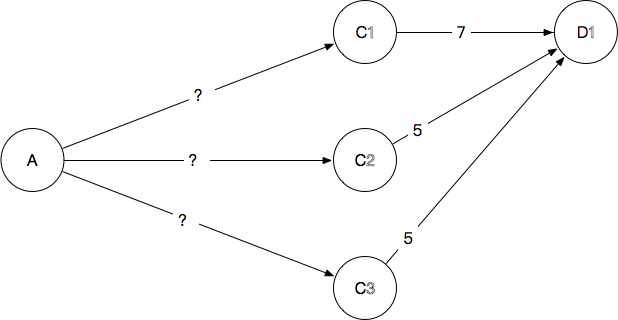
图5

这个图是不是和图3非常相似？

问题相应就变成了从A到每一个C的最短路径是多少？

解决了这个问题的话，我们就可以知道，最终如果走了比如$D_1$，前面路过的到底是哪个C

再进一步递推：为了确定到某一个C的最短路径，我们需要确定的就是这个问题：

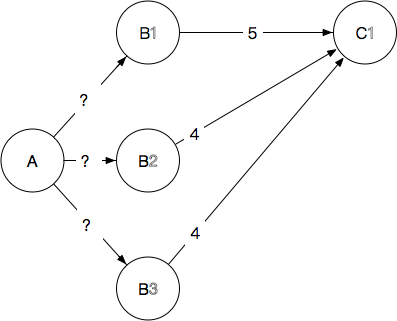
图6

不不不！聪明的你（O__O”…）一定发现了，这根本算不得什么问题，因为其实它是这样的：

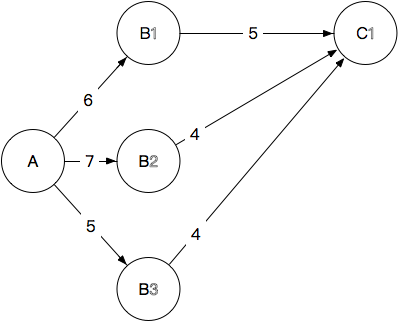
图7

因为我们已经推到最后一步了！从A到每一个B的路径事实上都是已知的，我们只需要把他们加在一起去比较大小就可以了！

别忘了我们的目标是什么：我们事实上是要确认如果最终路过了$C_1$，前面路过的是哪一个B。

从动态规划的角度考虑，假设我们最终的路径能路过$C_1$而我们已经走到了$C_1$，那么可以肯定地说，我们来到$C_1$的路径一定是所有来到$C_1$路径里面最短的那一条（在这个图上看应该是$B_3$）。因为如果我们没有走最短的那一条（比如我们错走成了$B_1$），那么我们只要用更短的那一条（$B_3$）去替换也一样可以走到$C_1$。

别倒立了，我们再从头想一下这个问题！

我们刚才是从最终的E节点倒推考虑的这个问题，这一次我们从A真正的走一遍。

我们是怎么走过来的

我们在每一层$M$都仅仅需要考虑这样一个问题：

为了到下一个层的某一个确定的节点$N_i$，我们到底应该从哪一个$M_i$出发呢？

一旦确定了从哪一个$M_i$出发，其他的$M_j$就不在我考虑范围内了。
就像我们刚才说的，只要我能找到去$C_1$应该从$B_3$走，我就不需要考虑其他的到$C_1$的路径了。这样就大大的减少了路径总数。

来，我们从A开始走

1. $A\rightarrow B$
   这个没啥说的：6，7，5

   我们顺利走到了B层

2. $A \rightarrow B \rightarrow C$
   我们确定到每一个C的节点，应该路过哪一个B：
   
   

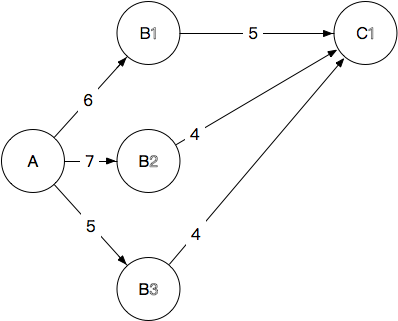
   • $C_1$:6+5=11, 7+4=11, 5+4=9，最终选择$A\rightarrow B_3 \rightarrow C_1$，抛弃其他到$C_1$的路径，长度9
   • $C_2$:12 ,10 ,11， 最终选择$A\rightarrow B_2 \rightarrow C_2$，抛弃其他到$C_2$的路径，长度10
   • $C_3$:15,14,11，最终选择$A\rightarrow B_3 \rightarrow C_3$，抛弃其他到$C_3$的路径，长度11
     

   我们顺利走到了C层，同时得到了到每一个C的最短路程

3. $A (\rightarrow B) \rightarrow C \rightarrow D$
   我们确定到每一个D的节点，应该路过哪一个C
   
   

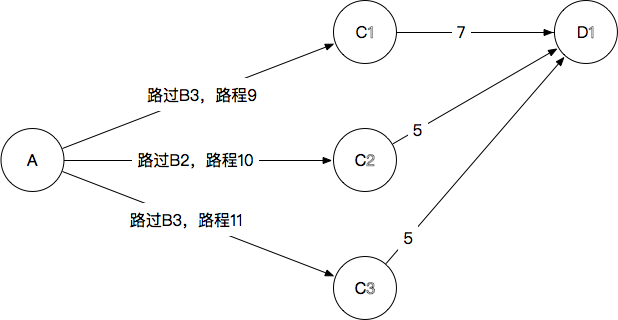
   • D_1:9+7=16,10+5=15,11+5=16,最终选择$A\rightarrow B_2 \rightarrow C_2 \rightarrow D_1$，抛弃其他到$D_1$的路径，长度15
   • D_2:17,14,18，最终选择$A\rightarrow B_2 \rightarrow C_2 \rightarrow D_2$，抛弃其他到$D_2$的路径，长度14
   • D_3:12,13,17，最终选择$A\rightarrow B_3 \rightarrow C_1 \rightarrow D_3$，抛弃其他到$D_3$的路径，长度12
     

   我们顺利走到了D层，同时得到了到每一个D的最短路程

4. $A (\rightarrow B \rightarrow C) \rightarrow D \rightarrow E$
   我们确定每一个D到最终节点E的路程
   
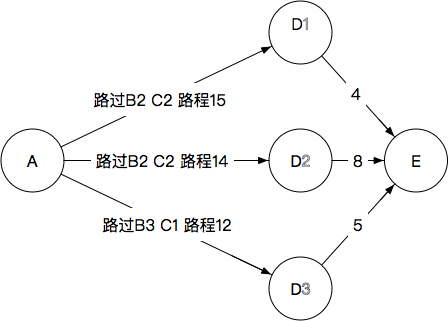
   显然最后应该选择$D_3$，完整路径为
   $A\rightarrow B_3 \rightarrow C_1 \rightarrow D_3 \rightarrow E$
   路程为17。抛弃其他所有路径。

这次我们需要算的次数大约是多少呢？

简单来说，从A到B有3条路径，每一条我们需要算到每一个C的最短距离，所以是$2(路径加法数)\times 3(A\rightarrow B)\times 3(B\rightarrow C)$，只要我们确定了每一个到C的最短距离剩下的事情就可以从C开始考虑了：每一个C需要确定到每一个D的最短距离，最终再加上D到E的距离就搞定了($2(路径加法数)\times 3(C个数)\times 3(D个数)$)。
如果换成是12层，每层最多13节点的话，每推一步的计算量最大规模在$13^2$（为了确定从哪一个B来到C，需要对每一个B到每一个C进行一次计算，上述计算每步是$3^2=9$次），而因为子问题都是一样的，所以增长是与网络长度成正比的：推进12次也仅仅乘以12而已。当然计算的方式不可能像这样简单乘一乘就搞定，但是可以看得出要比穷举要简单得多了。

We are almost there!

这几乎就是维特比算法了。至于维特比算法更公式化的描述和在隐含马尔科夫过程中的应用，我们下一文再说！