概率密度函数及其在信号方面的简单理解(上)概率密度函数
- 上篇 概率密度函数
-
- 1 离散随机变量与连续型随机变量
- 2 离散随机变量的分布函数
-
- 2.1 概率函数
- 2.2 概率分布
- 2.3 概率分布函数(累积分布函数!)
- 3 连续型随机变量的概率密度函数
- 4 Q&A
- 5 参考文献
从大二以来一直有三个“密度”相关的概念困扰着我,分别为:概率密度函数,频谱密度函数和功率谱密度。这仨都有“密度”二字,有啥区别与联系?总是心心念念着他们,最近又琢磨起此事,查了很多帖子论坛发现很少有把这三者结合起来讨论的,那行,我就来做吧,就按自己的想法写下了一些简单的理解。如有错误,欢迎指正。
本篇分为上中下三部分:上篇是对概率密度函数相关的基础的理解;中篇为频谱密度函数的简单理解,下篇为功率谱密度的简单理解。
上篇借鉴了“应该如何理解概率分布函数和概率密度函数?”等几篇文章,感谢几位原作者。链接见文末。
上篇 概率密度函数
1 离散随机变量与连续型随机变量
说到概率密度函数咱就不得不谈起概率分布函数了,要想理解概率分布函数与概率密度函数,我们要先从离散型随机变量和连续型随机变量说起。
若某种随机变量在一定区间内变量取值是有限个数或数值可以一一列举出来,那么称这种随机变量为离散型随机变量(Discrete random variable)。比如说抛一枚硬币,只可能出现正面和反面这两种情况;新生儿性别只有男女两种;掷一枚骰子,只可能出现1,2,3,4,5,6这六种情况。
连续型随机变量(Continuous random variable),书上是这样定义的:
连续型随机变量是指分布函数可以表示成变上限积分形式,因为变上限积分是连续的,所以分布函数是连续的。
等等,这句话有点不好理解,别急,咱换种说法理解一下。也可以这样说,连续型随机变量具有这样的性质:它在一定区间内变量取值为无限个或数值无法一一列举出来(注意:该性质是必要条件不是充分条件,这样说只是为了便于理解)。比如说某电子元件寿命,某地区健康男性成人的身高值,体重值等等。
形象点来解释:
画一幅画,左边是梯子,右边是斜坡。
像梯子一样能说出有多少层的,可描述的,是离散型随机变量;
像斜坡一样不能说出有多少层阶梯,不可描述的,是连续性随机变量。
需要注意的是,实际操作中梯子的阶高可能很小,看起来很像斜坡,需要放大看。
如图1所示:
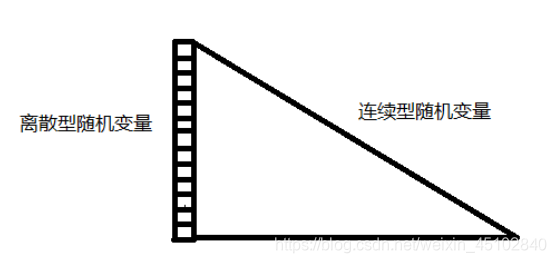
图1:离散型随机变量和连续型随机变量
2 离散随机变量的分布函数
注意:“研究一个离散型随机变量,不但要看它取哪些值,更重要的是看它取每个值的概率” 这句话是本篇的核心!!!这句话的核心是“概率”这俩字!!!
2.1 概率函数
首先从概率函数入手,顾名思义,概率函数就是用函数的形式表达概率。
Pi=P(X=i)(i=1,2,3,4,5,6)
在这个函数里,自变量X是随机变量的取值,因变量pi代表的是取值的概率,所以顺理成章的它就叫了X的概率函数。从公式上来看,概率函数一次只能表示一个取值的概率。比如P(X=1)=1/6,这表示随机变量取值为1的概率为1/6。
2.2 概率分布
概率分布,顾名思义,就是概率的分布,随机变量X的概率分布也经常被称为分布律(law of
distribution)。这里面我认为“分布”二字比“概率”二字更重要些。我们来看下面这张图
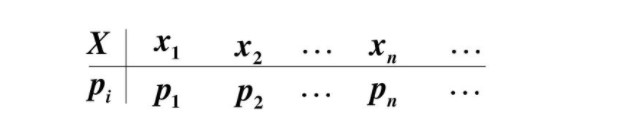
图2 离散型随机变量取值与其概率的分布列表
在很多教材中,这样的列表都被叫做离散型随机变量的“概率分布”或“分布律”。其实严格来说,它应该叫“离散型随机变量的值分布和值的概率分布列表”,这个名字虽然比“概率分布”长了点,但是肯定好理解了很多。因为这个列表,上面是值,下面是这个取值相应取到的概率,而且这个列表把所有可能出现的情况全部都列出来了!
举个例子吧,一颗6面的骰子,有1,2,3,4,5,6这6个取值,每个取值取到的概率都为1/6。那么你说这个列表是不是这个骰子取值的”概率分布“?

图3 掷骰子取值与其概率的分布列表
长得挺像的,上面是取值,下面是概率,这应该就是骰子取值的“概率分布”了吧!大错特错!少了一个最重要的条件!对于一颗骰子的取值来说,它列出的不是全部的取值,把6漏掉了!
注意:分布函数不只可以描述离散型随机变量,也可以描述连续型随机变量。
2.3 概率分布函数(累积分布函数!)
概率函数和概率分布刚刚都说完了,现在该来说说概率分布函数了,我觉得用累积概率函数或者累积分布函数更能表达含义,为什么呢?看下面这张图

图4 概率分布函数定义
我们来看看图上的公式,其中的F(x)就代表概率分布函数啦。这个符号的右边是一个长的很像概率函数的公式,但是其中的等号变成了小于等于号的公式。你再往右看看,这是一个一个的概率函数的累加!
发现概率分布函数的秘密了吗?它其实根本不是个新事物,它就是概率函数取值的累加结果!所以它又叫累积概率函数或者累积分布函数CDF(Cumulative distribution function)!(哎,为啥书上不直接写累积概率函数或者累积分布函数那?非要写个概率分布函数捉弄人,容易让人疑惑,维基百科上就直接写的Cumulative distribution
function)
所以说,概率函数和概率分布函数就像是一个硬币的两面,它们都只是描述概率的不同手段!
3 连续型随机变量的概率密度函数
你会不会有些疑惑,咱不是讲概率密度函数的吗?那刚刚说那么一大堆分布函数,累积密度函数想干嘛呢?别急,往下看!
如果理解了离散型随机变量及概率分布函数,那么接下来的就好理解了。从离散型随机变量变化到连续型随机变量,“概率分布”相应变化为“概率密度函数(Probability density function)”。概率密度函数就是概率密度。
教科书上对概率密度的定义是这样的:

图5 概率密度函数定义
要还是看不明白,别着急,我换种方式来解释一遍:(忍不住吐槽一下教材,喜欢写一堆抽象的难以理解的话,舍不得来点儿通俗易懂的解释。)
抛去书中晦涩难懂的概念定义,我们来通俗易懂的理解下:想象一下面前有一根密度分布不均匀的无限长金属棒,他的总质量为1,概率密度就相当于这根金属棒某处的密度,密度值可能接近0,也可能大于1或者很大。但是这个密度乘以体积所得的质量是恒小于等于1的。若某一点的概率密度越大,说明单位体积落在该点的质量越大。(也就是说事件发生在这个点的概率越大,再比如随手向靶子投飞镖,投到1环区域的概率远大于投进10环区域的概率)
看完上面金属棒的例子,估计对概率密度有个清晰的认识了吧,那下面我们来举几个常见的例子。
举列子之前我们先看一下之前教材上的定义,公式里可以看出:概率密度f(t)是累积分布函数F(X)的导函数,累积分布函数F(X)是概率密度f(t)的积分。
(以下例子均摘自维基百科)
例1: 均匀分布Uniform distribution :
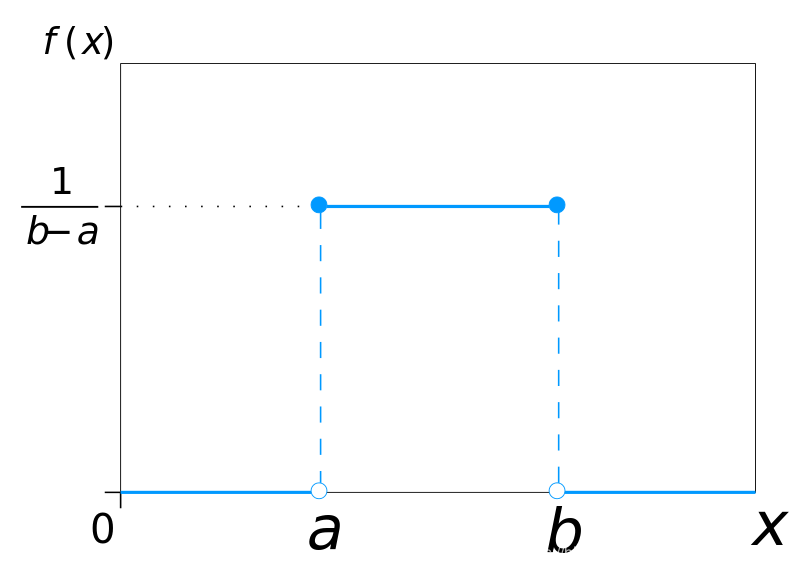
连续均匀分布的概率密度函数表示如下:
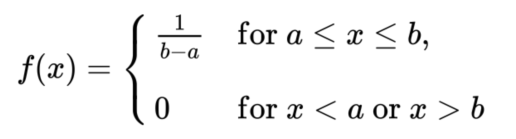
图6概率密度函数f(t)
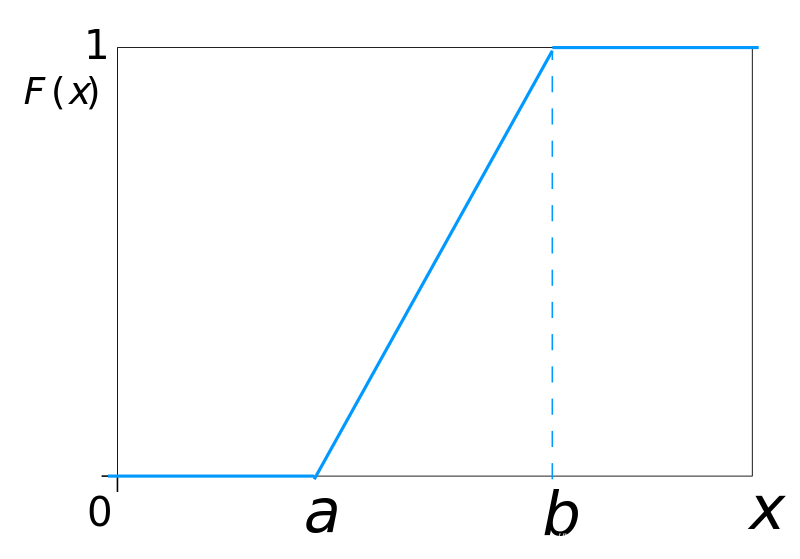
图7累积分布函数F(X)
如图6,7所示,分别为概率密度f(x)和累积分布函数F(X),可理解为该金属棒的密度分布是均匀的。看图可以直接看出f(x)和F(X)互为积分和导数关系。
例2:正态分布 Normal distribution
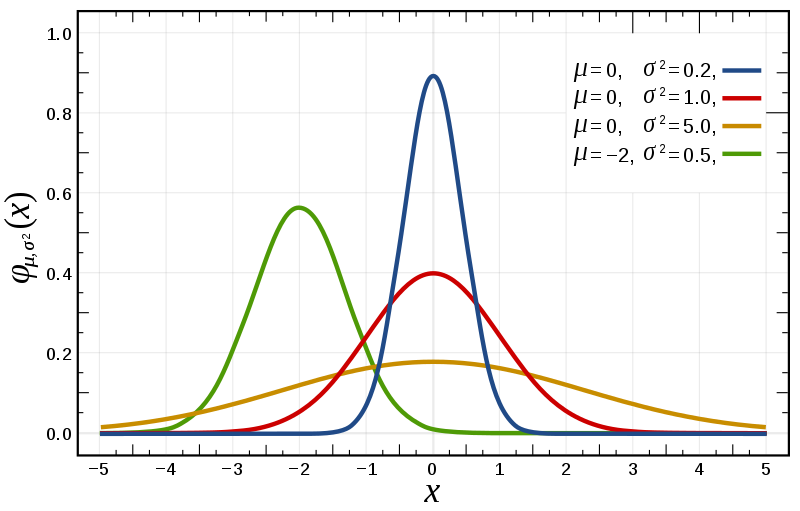
图8概率密度函数
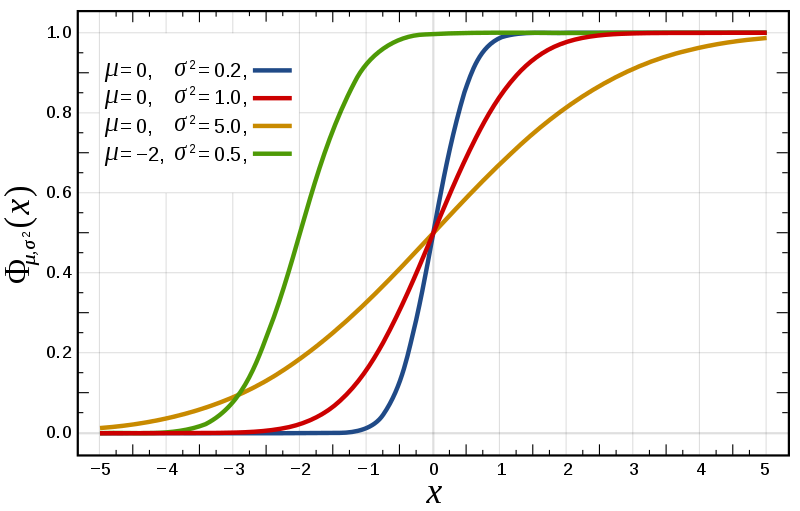
图9累积分布函数
如图8,9所示,红色曲线部分为标准正态分布,图中可以容易看出累积分布函数斜率最大处即为概率密度函数图像最高点。
4 Q&A
Q: 概率密度函数某一点代表的含义什么?
A: 某点的概率密度函数即为概率在该点的变化率(或导数)
概率与概率密度之间的关系可以理解为:距离和速度的关系,或者质量和密度的关系。
易错:
**概率密度函数上某点的值代表该事件发生的概率。❌错误❌
我们以距离和速度为例。
- 某一点的速度,不能以为是某一点的距离
- 某一点的距离没有意义,因为距离是从XX到XX的概念
- 因此,概率也需要个区间
上面的几句很好理解吧?到了概率这里也是换汤不换药的。
类比来说,概率密度函数图像上某一点x,不应该说在这一点上概率怎样,而应该说在该点附近的某一区间内,这个区间可以是x的邻域(可能趋近于0)。对x邻域内的f(x)进行积分,可以求得这个邻域的面积,该面积就代表了事件发生在这个区域内的概率。比起取一个点,我更倾向于取一个区域来理解,此时概率密度函数更有意义些。
5 参考文献
【1】概率论与数理统计-教材(第四版)盛骤
【2】https://blog.csdn.net/anshuai_aw1/article/details/82626468
【3】https://www.jianshu.com/p/b570b1ba92bb
【4】https://www.zhihu.com/question/263467674/answer/483484856
【5】https://www.zhihu.com/question/23237834/answer/470419391
【6】https://en.m.wikipedia.org/wiki/Uniform_distribution_(continuous)#
【7】https://en.m.wikipedia.org/wiki/Normal_distribution
以上均为自己的理解,可能有错误的地方,欢迎各位指正!!!