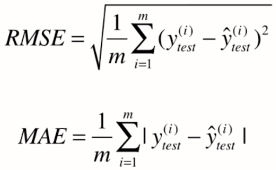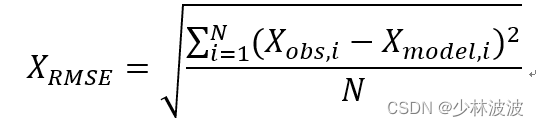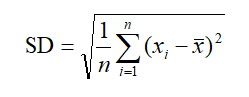概率密度函数估计

前导知识：【非参数估计—直方图法、Kn近邻估计法、Parzen窗法】

1. 最大似然估计

导包：

import numpy as np
from numpy.linalg import cholesky
import matplotlib.pyplot as plt
import random # 用于随机抽样

设置随机样本数：

# 设置随机样本数
sampleNo = 40;

一维数据处理：

mu = np.array([[1]])
Sigma = np.array([[2]])
R = cholesky(Sigma)
s = np.dot(np.random.randn(sampleNo, 1), R) + mu

随机抽样：

# 随机从40个样本中抽取20个样本
n = random.sample(s.tolist(),20)

均值估计：

# 均值估计
u = np.sum(np.array(n))/20
u

1.3770226175940825

方差估计：

# 方差估计
sigma = np.sum((np.array(n)-u)**2)/20
sigma

1.7032835324937676

二维数据处理：

mu = np.array([[2, 2]])
Sigma = np.array([[1, 0], [0, 4]])
R = cholesky(Sigma)
s = np.dot(np.random.randn(sampleNo, 2), R) + mu

随机抽样：

# 随机从40个样本中抽取20个样本
n = random.sample(s.tolist(),20)

均值向量估计：

# 均值向量估计
u = np.sum(np.array(n),axis=0)/20
u

array([2.052414  , 1.19130739])

协方差矩阵估计：

# 协方差估计
A = np.array(n)-u
B = np.transpose(A)
sigma = np.dot(B,A)/20
sigma

array([[0.43709834, 0.32039028],[0.32039028, 3.16173429]])

2. Parsen窗函数画法

matlab实现
主函数：

close all;clear all;
Samples = normrnd(0,1,1,10000); % 从正态分布中产生10000个均值为0，方差为1的样本
interval = -3:0.01:3; % 划定横纵坐标的范围index = 1;
for N = [1,10,100]for H = [0.25,1,4]p = Parsen(Samples,H,N,interval);subplot(3,3,index);plot(interval,p);hold on;plot(interval,normpdf(interval,0,1),'r-');legend(['h = ',num2str(H),' N = ',num2str(N)]);index = index + 1;end
end

Parsen函数：

function p = Parsen(Samples,H,N,interval)
% Samples 表示总样本
% h 表示Parsen窗口大小
% N 是随机采样的样本大小（1，10，100）
% x 是密度估计的点p = zeros(length(interval),1);
h = (H/sqrt(N)); % 半径for i = 1 : length(interval)b = 0;for j = 1 : Nu = (interval(i) - Samples(j))/h;b = b + exp(-u.^2/2)/(sqrt(2*pi)*h); % 一维高斯分布endp(i) = b / N;
end
end

图示：