1.说明

前序遍历: 先输出父节点，再遍历左子树和右子树
中序遍历: 先遍历左子树，再输出父节点，再遍历右子树
后序遍历: 先遍历左子树，再遍历右子树，最后输出父节点
小结: 看输出父节点的顺序，就确定是前序，中序还是后序

2.分析遍历的步骤

1.先创建一棵二叉树

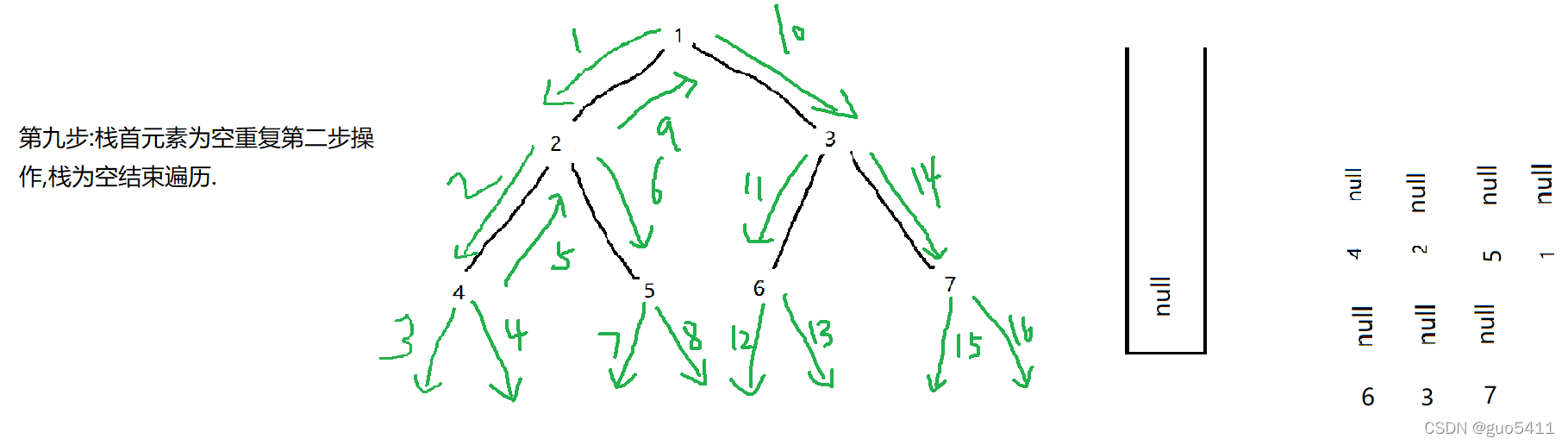
2.前序遍历

2.1 先输出当前结点(初始时为根结点root)

2.2 如果左子结点不为空，则递归继续前序遍历

2.3如果右子结点不为空，则递归继续前序遍历

3.中序遍历

3.1 如果当前结点左子结点不为空，则递归继续中序遍历

3.2 输出当前结点

3.3 如果当前结点右子结点不为空，则递归继续中序遍历

4.后序遍历

4.1 如果当前结点左子结点不为空，则递归继续后续遍历

4.2 如果当前结点右子结点不为空，则递归继续后续遍历

4.3 输出当前结点

3.代码实现

public class BinaryTreeDemo {public static void main(String[] args) {// 第三步：将结点连接形成二叉树(在main方法中实现)BinaryTree binaryTree = new BinaryTree();//创建需要的结点HeroNode root = new HeroNode(1, "宋江");HeroNode heroNode2 = new HeroNode(2, "吴用");HeroNode heroNode3 = new HeroNode(3, "卢俊义");HeroNode heroNode4 = new HeroNode(4, "关胜");HeroNode heroNode5 = new HeroNode(5, "林冲");// 注意binaryTree.setRoot(root);//手动创建二叉树root.setLeft(heroNode2);root.setRight(heroNode3);heroNode3.setLeft(heroNode4);heroNode3.setRight(heroNode5);//测试遍历System.out.println("前序遍历");binaryTree.preOrder();// 1 2 3 4 5System.out.println("中序遍历");binaryTree.infixOrder();// 2 1 4 3 5System.out.println("后序遍历");binaryTree.postOrder();// 2 4 5 3 1}}
// 第一步：先创建HeroNode结点
// 第二步：创建二叉树
// 第三步：将结点连接形成二叉树(在main方法中实现)// 第二步：创建二叉树
class BinaryTree{// 定义根结点private HeroNode root;// 创建根结点public void setRoot(HeroNode root){this.root = root;}// 前序遍历public void preOrder(){if (this.root != null) {this.root.preOrder();} else {System.out.println("二叉树为空，不能遍历");}}// 中序遍历public void infixOrder(){if (this.root != null) {this.root.infixOrder();} else {System.out.println("二叉树为空，不能遍历");}}// 后序遍历public void postOrder(){if (this.root != null) {this.root.postOrder();} else {System.out.println("二叉树为空，不能遍历");}}}//第一步：先创建HeroNode结点
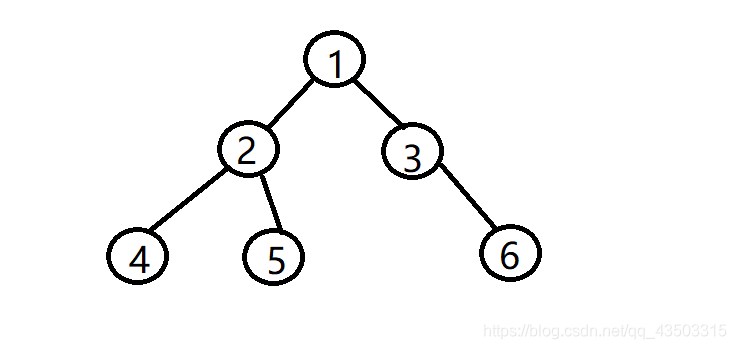
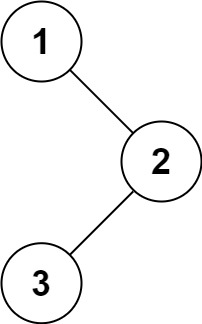
class HeroNode{private int no;private String name;private HeroNode left;//左子结点，默认值为nullprivate HeroNode right;//右子结点public HeroNode(int no, String name) {this.no = no;this.name = name;}public int getNo() {return no;}public void setNo(int no) {this.no = no;}public String getName() {return name;}public void setName(String name) {this.name = name;}public HeroNode getLeft() {return left;}public void setLeft(HeroNode left) {this.left = left;}public HeroNode getRight() {return right;}public void setRight(HeroNode right) {this.right = right;}@Overridepublic String toString() {return "HeroNode [no=" + no + ", name=" + name + "]";}// 编写前序遍历的方法public void preOrder(){// 输出当前结点System.out.println(this);//递归遍历左子结点if (this.left != null) {this.left.preOrder();}//递归遍历右子结点if (this.right != null) {this.right.preOrder();}}//编写中序遍历的方法public void infixOrder(){//递归遍历左子结点if (this.left != null) {this.left.infixOrder();}//输出当前结点System.out.println(this);//递归遍历右子结点if (this.right != null) {this.right.infixOrder();}}//后序遍历public void postOrder(){//遍历左子结点if (this.left != null) {this.left.postOrder();}// 遍历右子结点if (this.right != null) {this.right.postOrder();}// 输出当前结点System.out.println(this);}}

4.测试代码中二叉树图

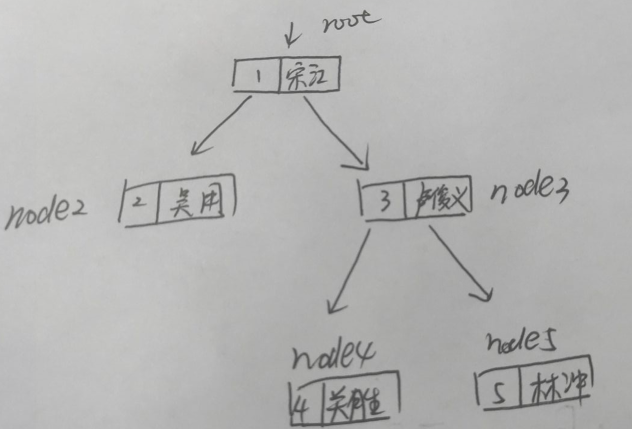
1659965172355

求二叉树的深度

//求二叉树的深度public int getDepth(HeroNode root) {int LD,RD;//左二叉树，右二叉树的深度if (root == null) {return 0;}else {LD = getDepth(root.getLeft());RD = getDepth(root.getRight());return (LD>RD ? LD : RD) +1;}}