二叉树的前序遍历

对于一颗二叉树，当遍历它的时候使用
递归总是轻而易举的。

这是二叉树前序遍历-使用递归

public void preorderTraversal(TreeNode root){if(root==null)return;System.out.print(root.data+"  ");preorderTraversal(root.left);preorderTraversal(root.right);}

1.简单几行代码就可以将一颗二叉树遍历完但是递归其中的运算是如何的，我们不需要知道，计算机会用函数栈自己解决，初学递归时，会陷入一种困境，我们总是想钻进递归方法里把每一步都缕清，事实上人脑是不可能把每一步的结果都想出来的，就算写在纸上也无法思考清楚。当然，我们也不需要去钻今递归代码里，我们只需要明白递归用来干什么就行。2.在二叉树的前序遍历中，我们知道前序遍历是先打印根结点，再打印左子树，然后打印右子树。对于树中的每一个结点都符号这个要求，我们不需要关心左子树还有左子树，左子树还有右子树，右子树还有右子树等等无穷无尽的问题因为每一个结点都必须遵守这样的规定，同样，我们也无需过分关心结点为空怎么办空结点的处理应该是细节问题，它不影响前序遍历的规定，放过细节，关心策略。

二叉树和前序遍历-迭代

1.那么当不用递归处理，改用循环迭代进行前序遍历，我们该怎么做呢？2.我们应该关心每一个结点是否应该被
打印输出？关心它的下一个结点该打印哪一个？关心当处理到空结点时候怎么办吗？这些问题都不是我们初步要考虑的，可能会有细节问题，不过细节在代码完善时候再考虑也不迟3.我们只需要明白策略即可。对于二叉树前序遍历，我们知道它的遍历规则，那么我们定义一个	策略【root】

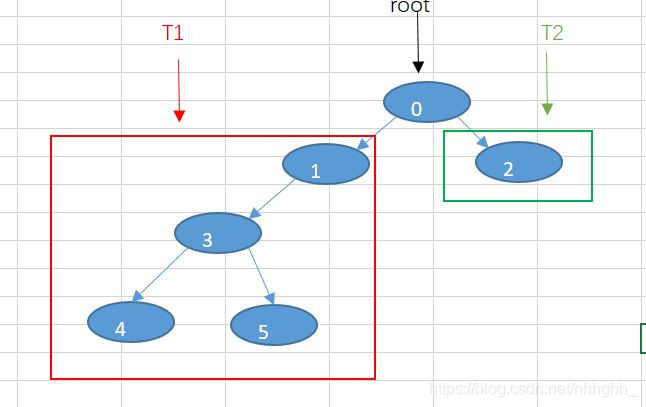
1.我们把二叉树分成三个部分，root结点表示需要当前要打印的的结点，T1表示左子树，T2表示右子树
2.我们不用知道T1或者T2树里面是如何按序打印值的，从总体上看我们只要先打印root，再打印左子树，然后右子树就行了。
3. 策略【root】：表示的就是这种规则，先打印root，再打印T1，再打印T2。它对于每一个结点都适用这种策略
4. 那我们可以轻而易举地写出这种伪代码

	while(root){//打印本结点System.out.print(root.data+"  ");if(T1){打印T1}if(T2){打印T2}}

分析：
1. 每一颗右子树T2都比左子树T1晚打印，我们使用Stack栈来先存放T2树，再存放T1树，这样从整体上看T1树在栈顶将会先释放。

	while(root){//打印本结点System.out.print(root.data+"  ");if(root.right!=null){stack.push(root.right);}if(root.left!=null){stack.push(root.left);}}

这样我们的思维就出来了，先打印root结点，有右子
结点就压入栈，先处理左子结点总体思维有了后，我们处理细节部分，
1. while循环是会接受一个root结点，表示要处理的树的根结点，那么root!=null是while的入口条件，同样如果root结点下没有子结点，也就是说Stack栈没有存放子树那么也就说明栈为空代表无子树迭代结束,!stack.isEmpty()也是while的入口条件2. 每一次进入循环的root是如何确定的？我们知道当第一个root结点进入循环，打印它，并把它的右子树，左子树压入栈

2.当root.left和root.right入栈操作完成后，无论是否都入栈(也许为空),我们的root都应该指向栈顶结点因为下一次循环进入的root就应该是栈顶结点3. 因为循环体内我们使用的是直接System.out结点这样造成栈顶元素无法释放，所以打印完结点后，直接释放栈顶元素

代码

public void preorderTraversal(TreeNode root,Stack<TreeNode> stack){while(!stack.isEmpty() || root!=null){System.out.print(root.data+"  ");if(!stack.isEmpty()){stack.pop();}if(root.right!=null){stack.push(root.right);}if(root.left!=null){stack.push(root.left);}root = stack.isEmpty() ? null : stack.peek();}}

总结

使用迭代对二叉树进行前序遍历，它的遍历策略不难理解，
但是循环的入口，出口并不是那么容易控制，迭代代码并
不难理解，但是很容易形成“一看就懂，一写就废”这篇对于迭代的理解帮助我们学习二叉树遍历时如何处理，
代码是数不尽样式的，但自己的思想却只有自己知道。