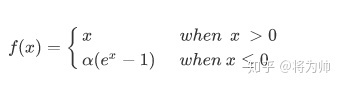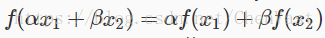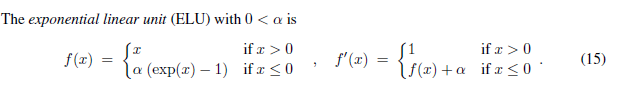22个激活函数，ReLU、RReLU、LeakyReLU、PReLU、Sofplus、ELU、CELU、SELU、GELU、ReLU6、Sigmoid、Tanh、Softsign、Hardtanh等

article/2025/9/21 16:59:19

转自：https://www.pianshen.com/article/33331174884/

1.22.Linear常用激活函数
1.22.1.ReLU torch.nn.ReLU()
1.22.2.RReLU torch.nn.RReLU()
1.22.3.LeakyReLU torch.nn.LeakyReLU()
1.22.4.PReLU torch.nn.PReLU()
1.22.5.Sofplus torch.nn.Softplus()
1.22.6.ELU torch.nn.ELU()
1.22.7.CELU torch.nn.CELU()
1.22.8.SELU torch.nn.SELU()
1.22.9.GELU torch.nn.GELU()
1.22.10.ReLU6 torch.nn.ReLU6()
1.22.11.Sigmoid torch.nn.Sigmoid()
1.22.12.Tanh torch.nn.Tanh()
1.22.13.Softsign torch.nn.Softsign()
1.22.14.Hardtanh torch.nn.Hardtanh()
1.22.15.Threshold torch.nn.Threshold()
1.22.16.Tanhshrink torch.nn.Tanhshrink()
1.22.17.Softshrink torch.nn.Softshrink()
1.22.18.Hardshrink torch.nn.Hardshrink()
1.22.19.LogSigmoid torch.nn.LogSigmoid()
1.22.20.Softmin torch.nn.Softmin()
1.22.21.Softmax torch.nn.Softmax()
1.22.22.LogSoftmax torch.nn.LogSoftmax()

1.22.Linear常用激活函数

1.22.1.ReLU torch.nn.ReLU()

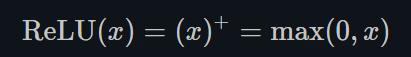
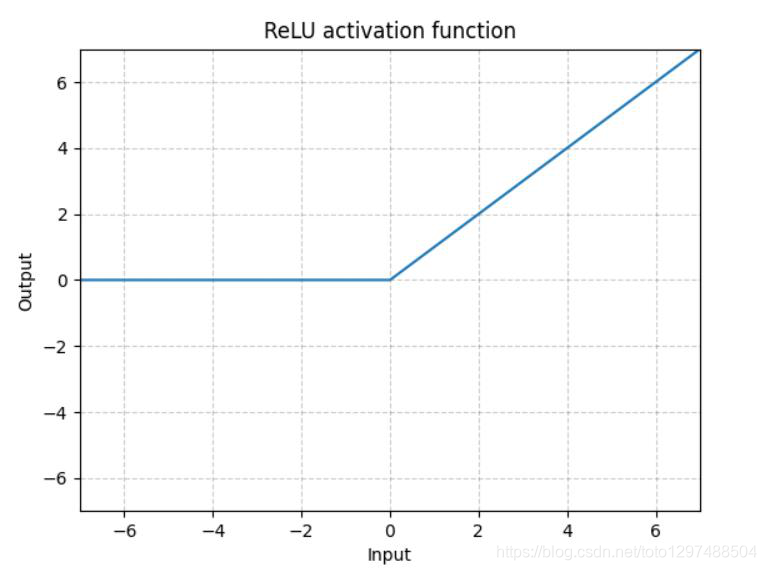
在这里插入图片描述
ReLU的函数图示如下:
在这里插入图片描述

1.22.2.RReLU torch.nn.RReLU()

ReLU有很多变种, RReLU是Random ReLU的意思，定义如下:
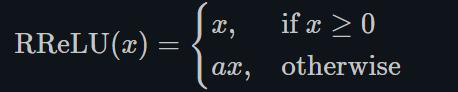
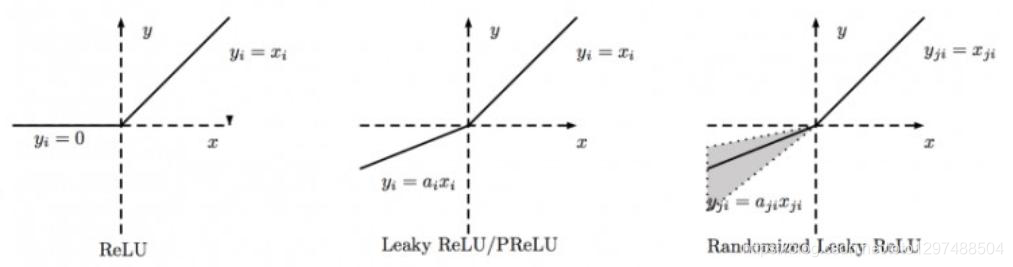
在这里插入图片描述
对RReLU而言, a是一个在给定范围内的随机变量(训练), 在推理时保持不变。同LeakyReLU不同的是，RReLU的a是可以learnable的参数，而LeakyReLU的a是固定的。
在这里插入图片描述

1.22.3.LeakyReLU torch.nn.LeakyReLU()

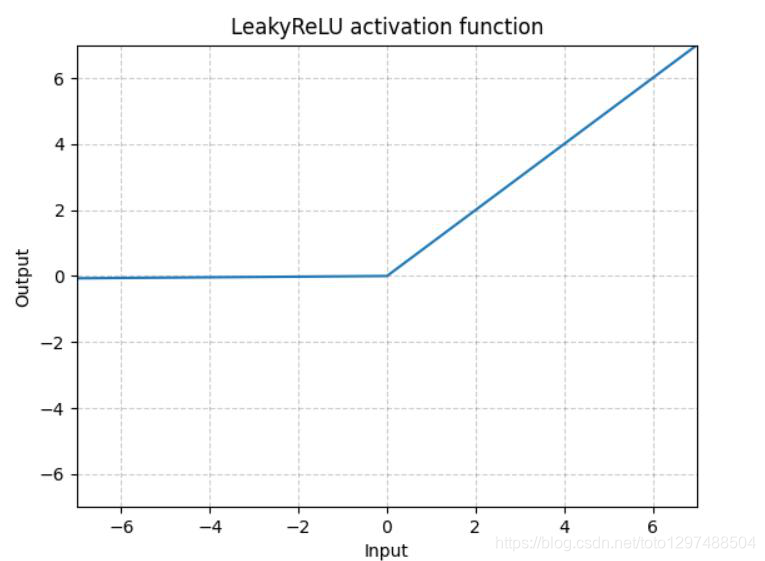
在这里插入图片描述
在这里插入图片描述
这里a是固定值，LeakyReLU的目的是为了避免激活函数不处理负值（小于0的部分梯度为0），通过使用negative slope，其使得网络可以在传递负值部分的梯度，让网络可以学习更多的信息，在一些应用中确实有较大的益处。

1.22.4.PReLU torch.nn.PReLU()

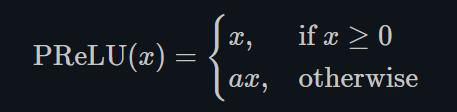
在这里插入图片描述
不同于RReLU的a可以是随机的，PReLU中的a就是一个learnable的参数。
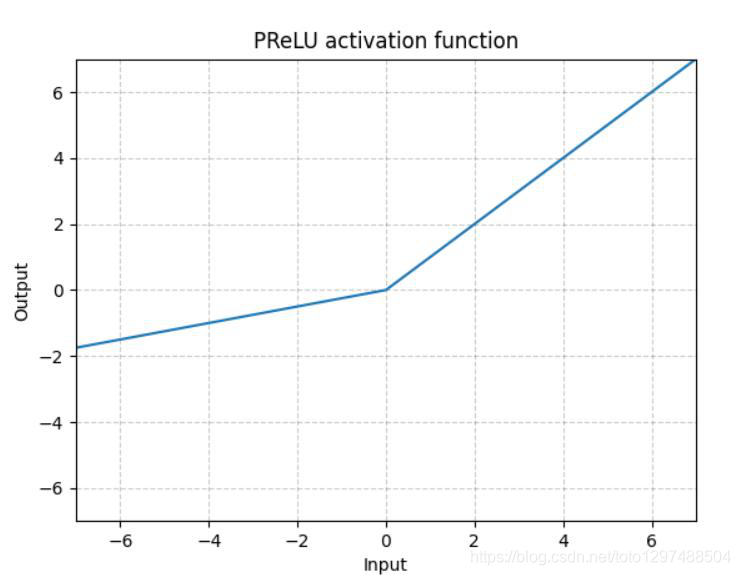在这里插入图片描述需要注意的是：上述激活函数（即ReLU、LeakyReLU、PReLU）是尺度不变（scale-invariant）的。

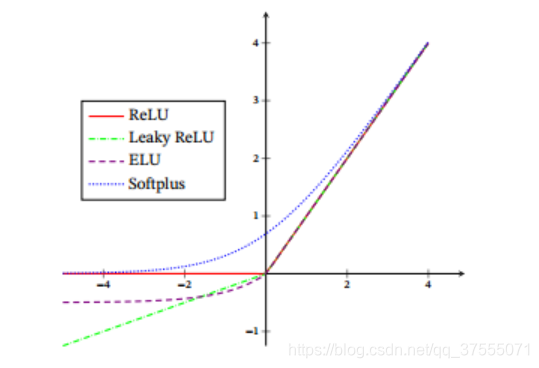
1.22.5.Sofplus torch.nn.Softplus()

Softplus作为损失函数在StyleGAN1和2中都得到了使用，下面分别是其表达式和图解。
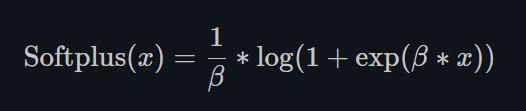
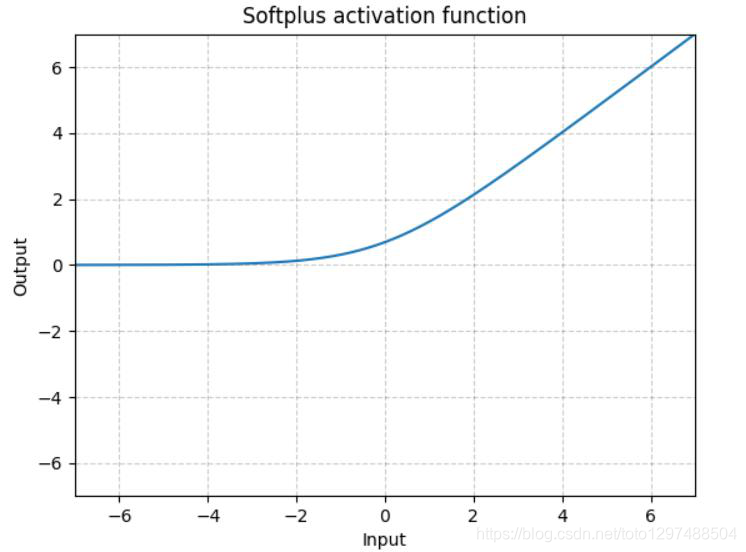
在这里插入图片描述
在这里插入图片描述

Softplus 是ReLU的光滑近似，可以有效的对输出都为正值的网络进行约束。
随着β的增加，Softplus与ReLU越来越接近。

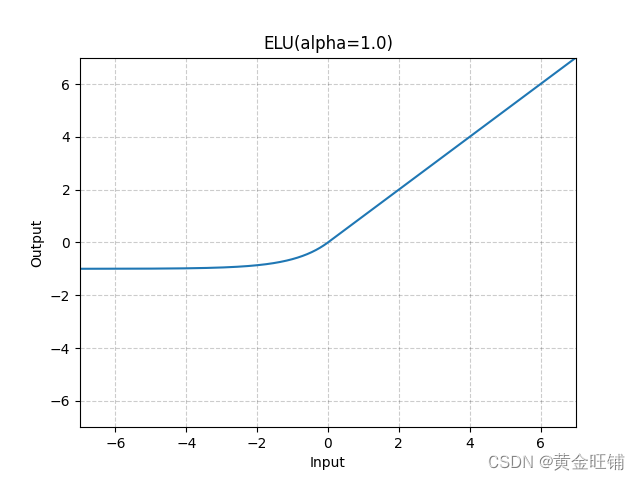
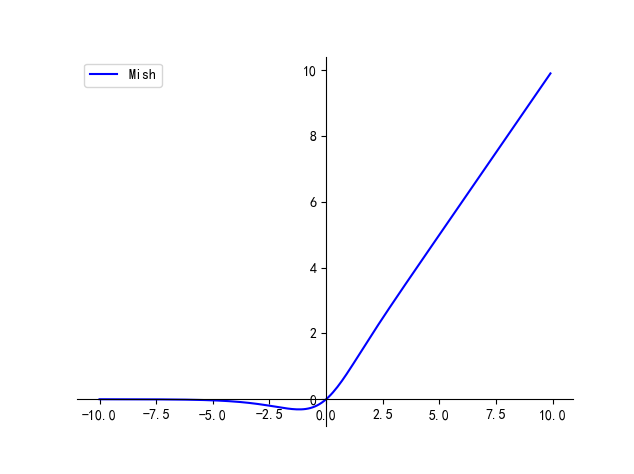
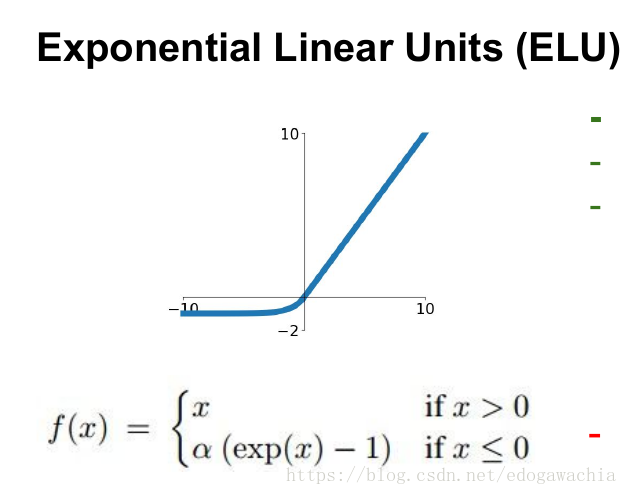
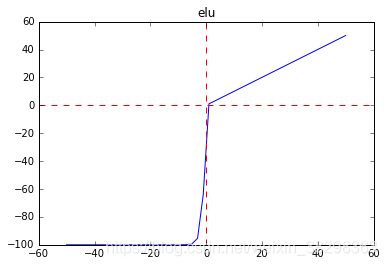
1.22.6.ELU torch.nn.ELU()

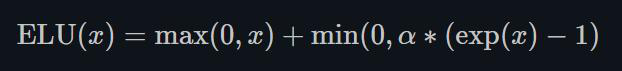
在这里插入图片描述
在这里插入图片描述
ELU不同于ReLU的点是，它可以输出小于0的值，使得系统的平均输出为0。因此，ELU会使得模型收敛的更加快速，其变种（CELU , SELU）只是不同参数组合ELU。

1.22.7.CELU torch.nn.CELU()

跟ELU相比，CELU是将ELU中的exp(x)变为exp(x/a)
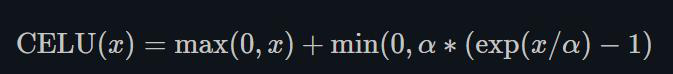
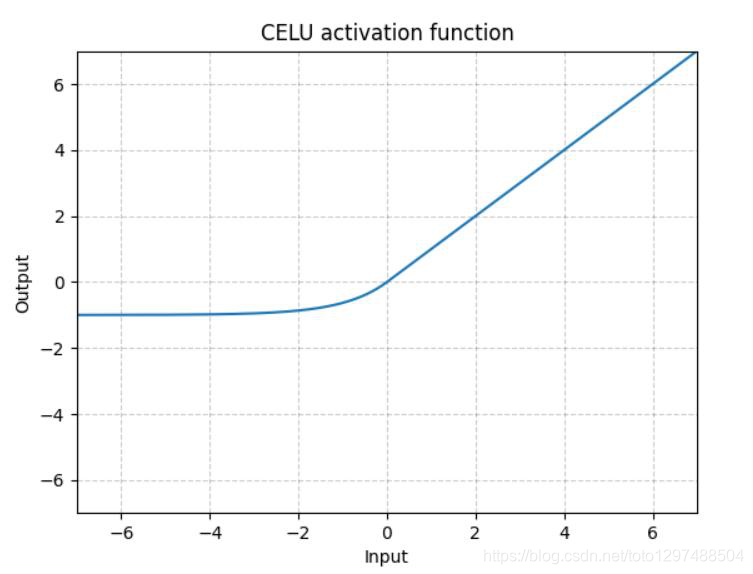
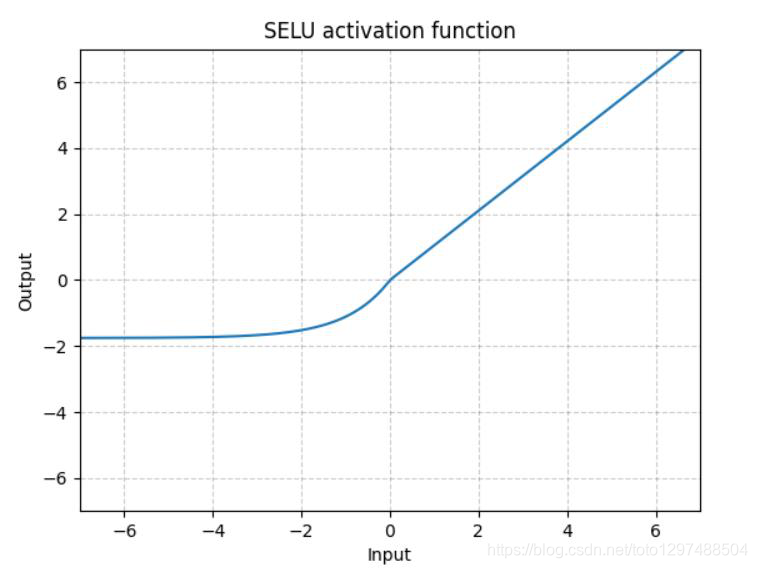
在这里插入图片描述
在这里插入图片描述

1.22.8.SELU torch.nn.SELU()

跟ELU相比，SELU是将ELU乘上了一个scala变量。
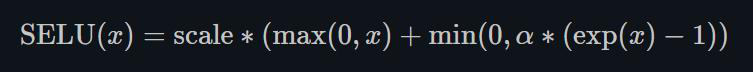
在这里插入图片描述
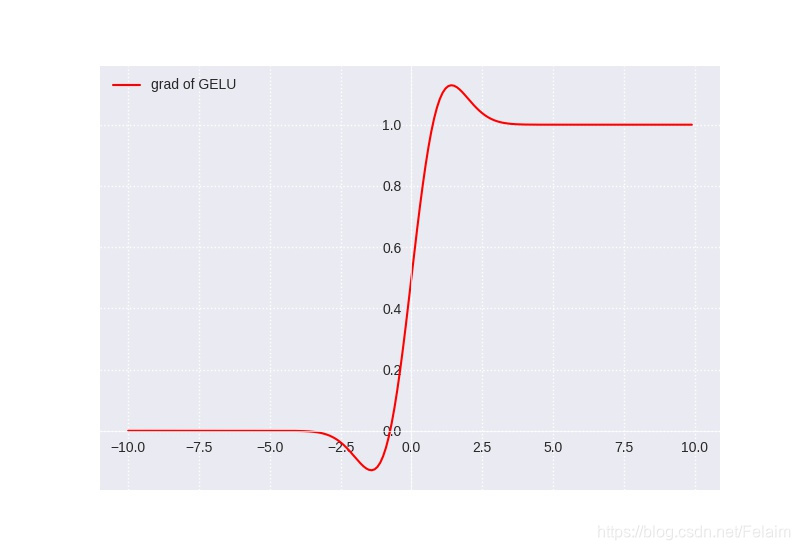
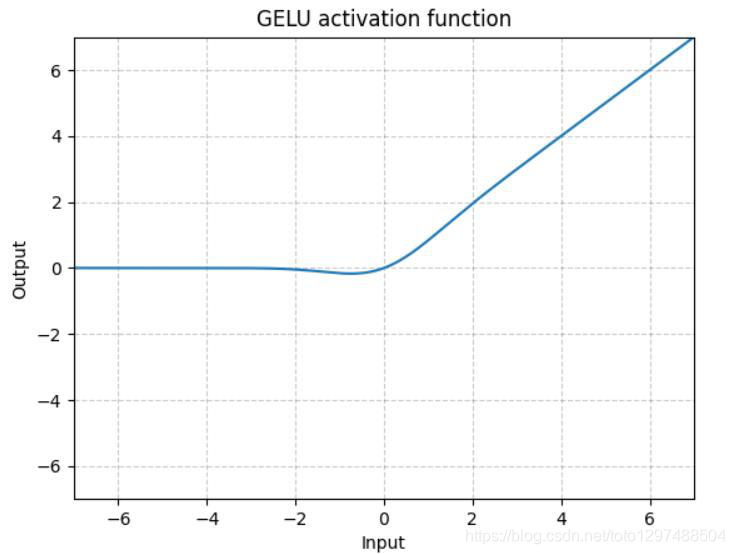
在这里插入图片描述

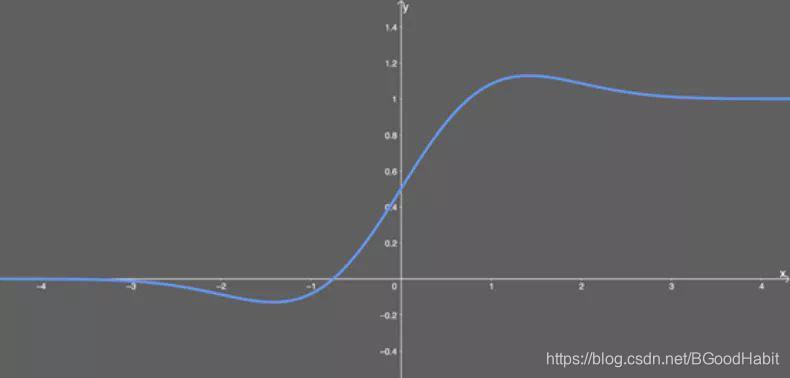
1.22.9.GELU torch.nn.GELU()

其中(x)Φ(x)是高斯分布的累积分布函数（Cumulative Distribution Function for Gaussian Distribution）。
在这里插入图片描述

1.22.10.ReLU6 torch.nn.ReLU6()

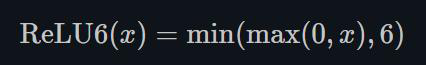
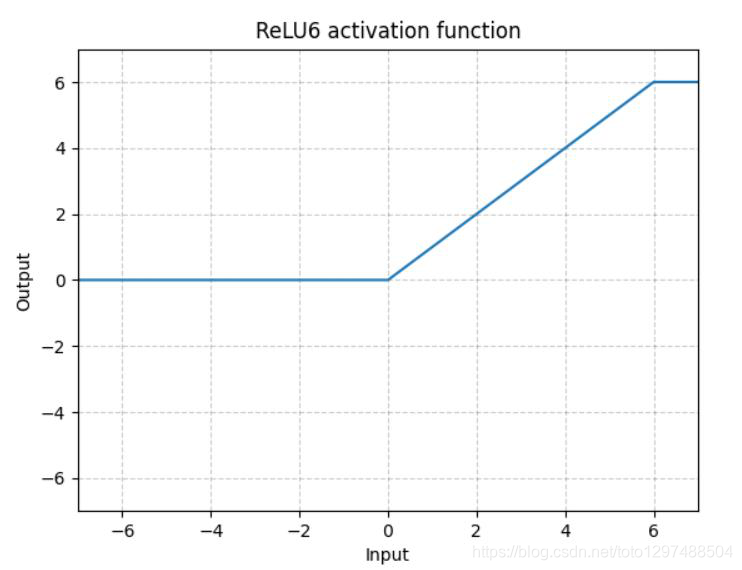
在这里插入图片描述
在这里插入图片描述
ReLU6是在ReLU的基础上，限制正值的上限6. one-stage的目标检测网络SSD中用这个损失函数。

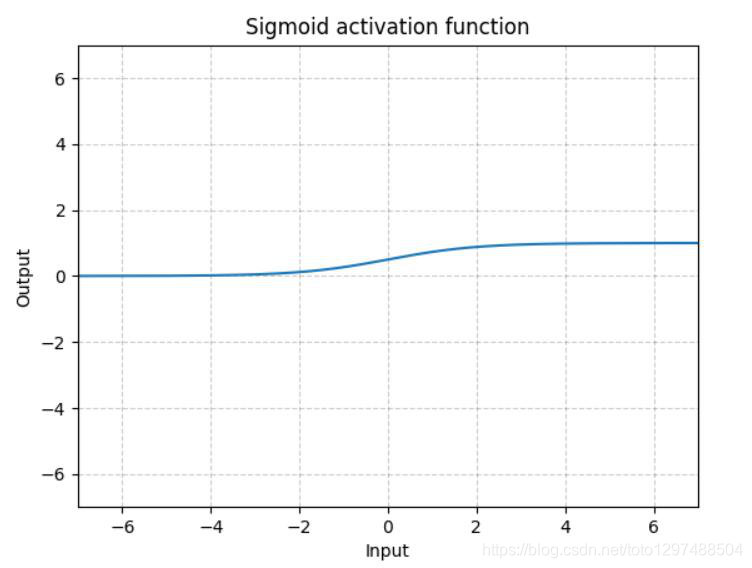
1.22.11.Sigmoid torch.nn.Sigmoid()

Sigmoid是将数据限制在0到1之间。而且，由于Sigmoid的最大的梯度为0.25，随着使用sigmoid的层越来越多，网络就变得很难收敛。

因此，对深度学习，ReLU及其变种被广泛使用避免收敛困难的问题。
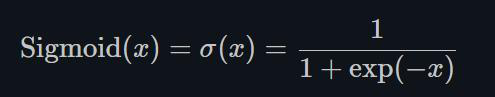
在这里插入图片描述
在这里插入图片描述

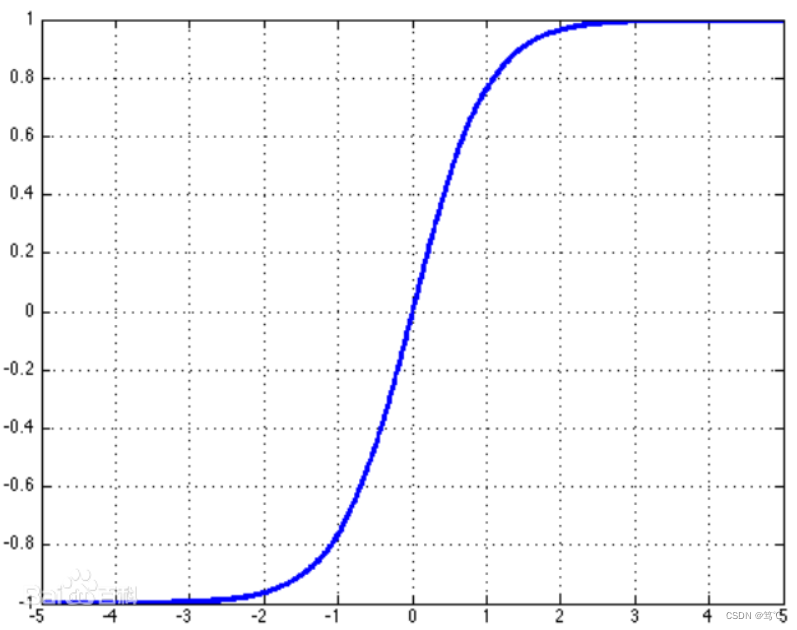
1.22.12.Tanh torch.nn.Tanh()

Tanh就是双曲正切，其输出的数值范围为-1到1. 其计算可以由三角函数计算，也可以由如下的表达式来得出：
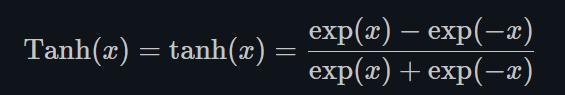
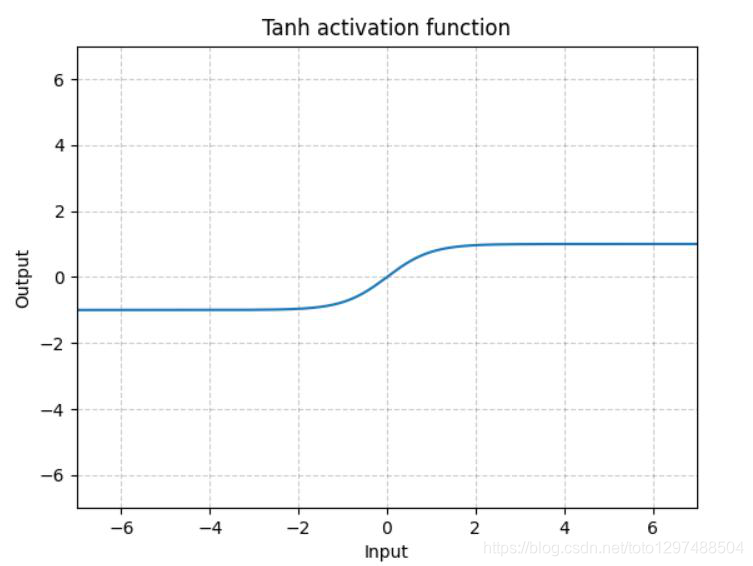
在这里插入图片描述
在这里插入图片描述
Tanh除了居中(-1到1)外，基本上与Sigmoid相同。这个函数的输出的均值大约为0。因此，模型收敛速度更快。注意，如果每个输入变量的平均值接近于0，那么收敛速度通常会更快，原理同Batch Norm。

1.22.13.Softsign torch.nn.Softsign()

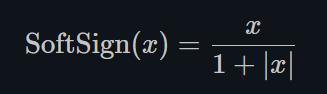
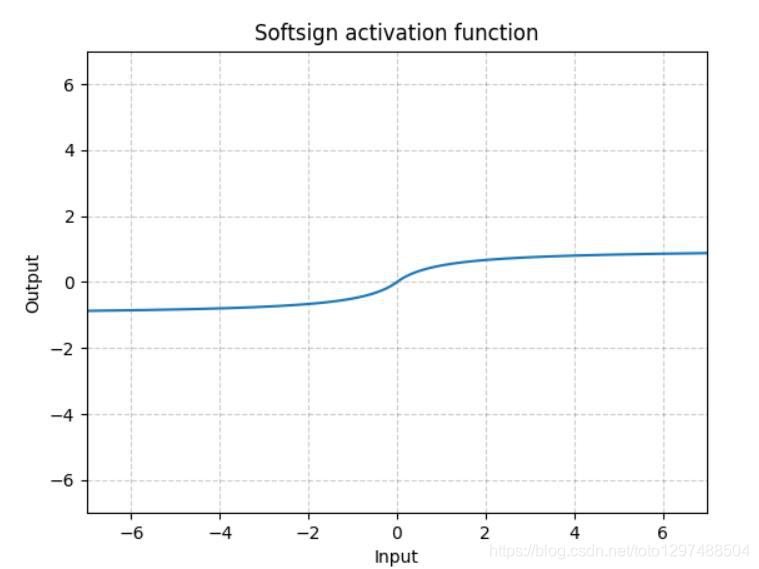
在这里插入图片描述
在这里插入图片描述
同Sigmoid有点类似，但是它比Sigmoid达到渐进线(asymptot n. [数] 渐近线)的速度更慢，有效的缓解了梯度消失的问题（gradient vanishing problem (to some extent).）。

1.22.14.Hardtanh torch.nn.Hardtanh()

如下图所示，Hardtanh就是1个线性分段函数[-1, 1]，但是用户可以调整下限min_val和上限max_val，使其范围扩大/缩小。
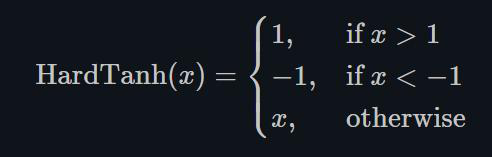
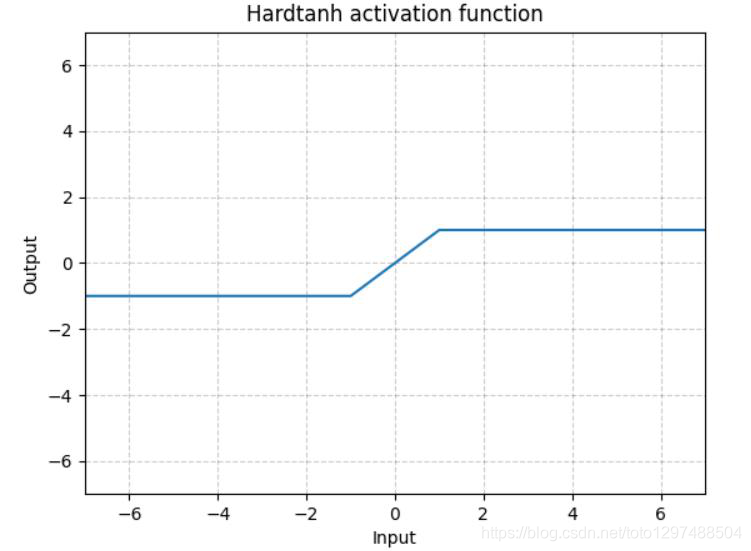
在这里插入图片描述
在这里插入图片描述
当权值保持在较小的范围内时，Hardtanh的工作效果出奇的好。

1.22.15.Threshold torch.nn.Threshold()

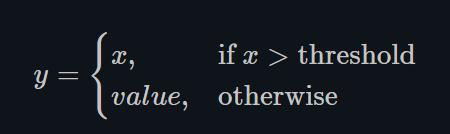
在这里插入图片描述

这种Threshold的方式现在很少使用，因为网络将不能传播梯度回来。这也是在60年代和70年代阻止人们使用反向传播的原因，因为当时的科研人员主要使用的是Binary的神经元，即输出只有0和1，脉冲信号。

1.22.16.Tanhshrink torch.nn.Tanhshrink()

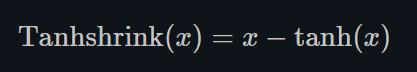
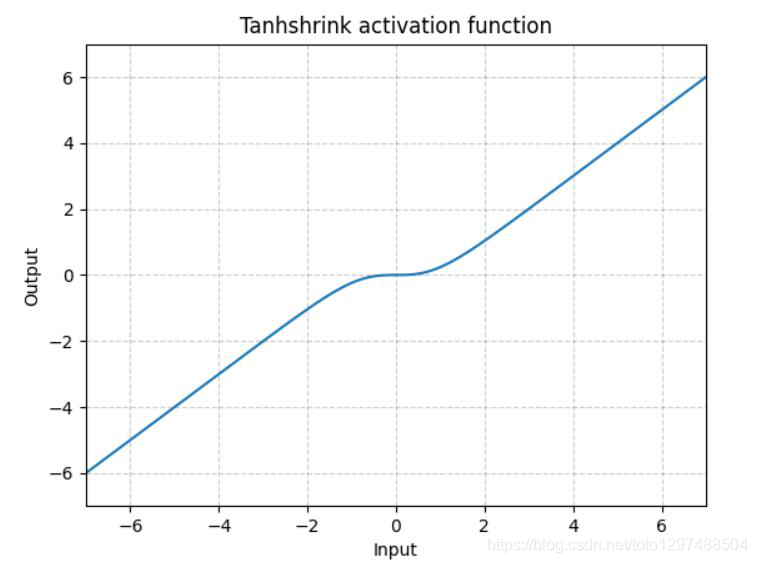
在这里插入图片描述
在这里插入图片描述
除了稀疏编码外，很少使用它来计算潜在变量(latent variable)的值。

1.22.17.Softshrink torch.nn.Softshrink()

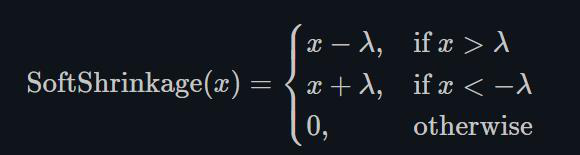
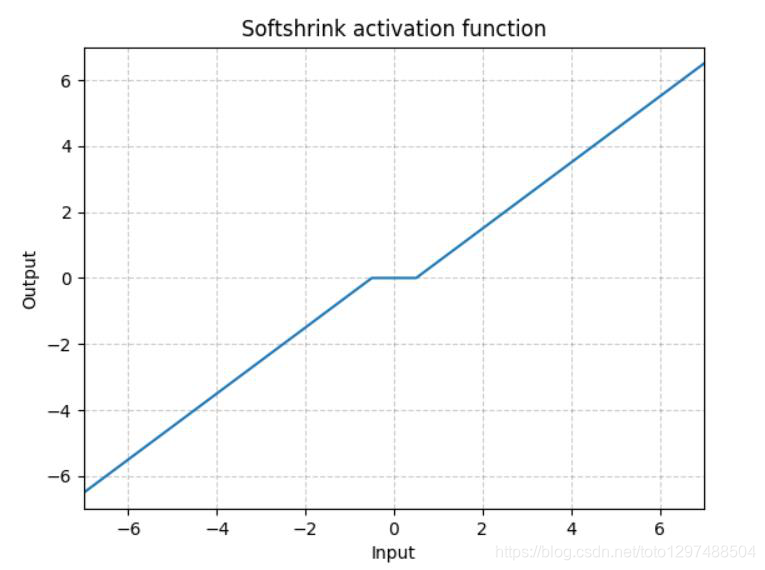
在这里插入图片描述
在这里插入图片描述
这种方式目前也不怎么常用，其目的是通过设置λ，将靠近0的值直接强制归0，由于这种方式对小于0的部分没有约束，所以效果不太好。

1.22.18.Hardshrink torch.nn.Hardshrink()

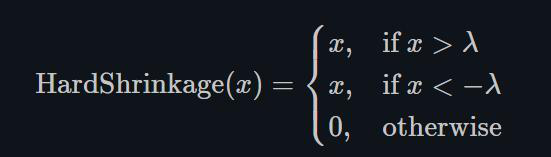
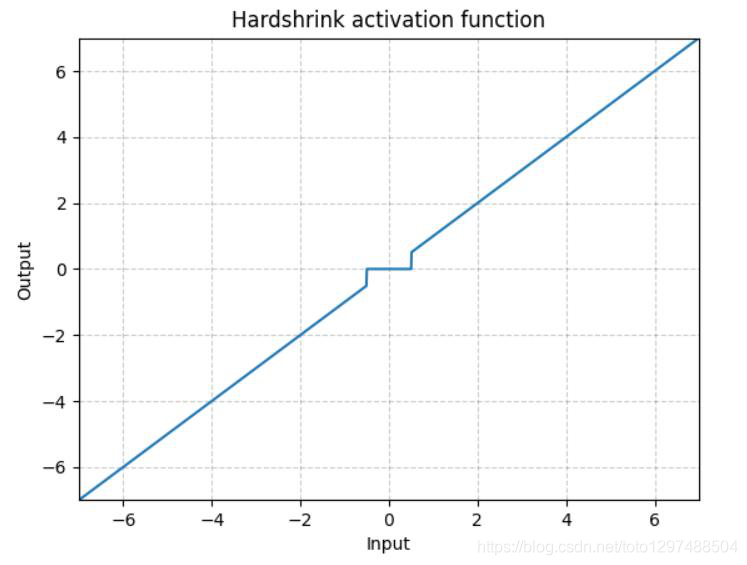
在这里插入图片描述
在这里插入图片描述
同Softshrink类似，除了稀疏编码以外，很少被使用。

1.22.19.LogSigmoid torch.nn.LogSigmoid()

LogSigmoid是在Sigmoid基础上，wrap了一个对数函数。
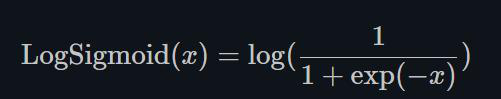
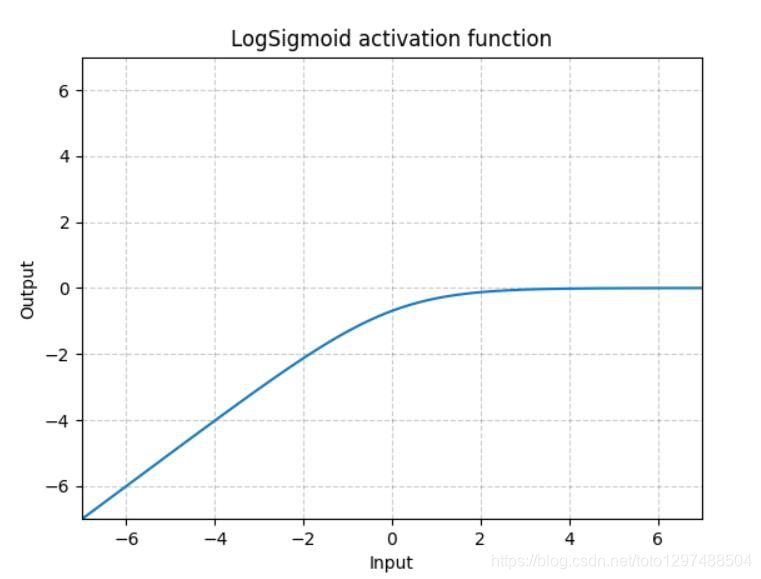
在这里插入图片描述
在这里插入图片描述
这种方式用作损失函数比较多

1.22.20.Softmin torch.nn.Softmin()

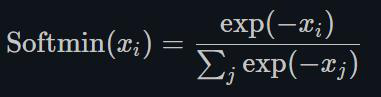
在这里插入图片描述

将数字变成概率分布，类似Softmax。

1.22.21.Softmax torch.nn.Softmax()

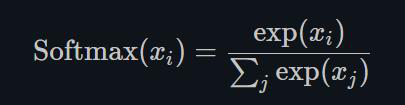
在这里插入图片描述

1.22.22.LogSoftmax torch.nn.LogSoftmax()

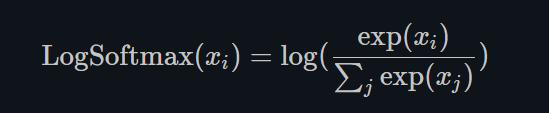
在这里插入图片描述
同LogSigmoid类似，LogSoftmax用作损失函数比较多


http://chatgpt.dhexx.cn/article/vmbSm83D.shtml

相关文章

常用激活函数（Sigmiod、Tanh、Softmax、ReLU、elu、LReLU、Softplus）函数表达式、特点、图像绘制（代码）---已解决

常用激活函数（Sigmiod、Tanh、Softmax、ReLU、elu、LReLU、Softplus）函数表达式、特点、图像绘制（代码）---已解决

楼主最近在研究激活函数，索性将常用的激活函数进行了简单的整理，方便以后翻看，也希望能帮到你。 1、sigmoid函数 函数表达式：f(x) 1/(1e^-x) 函数特点： 优点：1.输出[0,1]之间；2.连续函数&#…
阅读更多...
Sigmoid，tanh，Relu，Leaky ReLu，ELU，GeLu 激活函数理解

Sigmoid，tanh，Relu，Leaky ReLu，ELU，GeLu 激活函数理解

目录 1 神经网络为什么需要非线性激活函数？2 Sigmoid2.1缺陷2.1.1 梯度消失2.2.2 Output非zero-centered 3 Tanh3.1 缺陷 4 ReLu4.1 缺陷 5 Leaky ReLu6 ELU7 GeLu7.1 基础知识回顾7.1.1 正态分布7.1.2 概率密度函数7.1.3 累积分布函数7.1.4 Φ(x)与erf(x)函数关系公…
阅读更多...
Elu函数~小朋友

Elu函数~小朋友

Elu激励函数的数学表达式如下： 图一：摘自 https://blog.csdn.net/zrh_CSDN/article/details/81266188 代码如下： #code:utf-8import numpy as np import matplotlib.pyplot as pltdef elu(x,a):y x.copy()for i in range(y.shape[0]):if y[…
阅读更多...
【Python--torch（激活函数说明+代码讲解）】激活函数（sigmoid/softmax/ELU/ReLU/LeakyReLU/Tanh）

【Python--torch（激活函数说明+代码讲解）】激活函数（sigmoid/softmax/ELU/ReLU/LeakyReLU/Tanh）

【Python–torch】激活函数(sigmoid/softmax/ELU/ReLU/LeakyReLU/Tanh) 文章目录 【Python--torch】激活函数(sigmoid/softmax/ELU/ReLU/LeakyReLU/Tanh)1. 介绍2. 常用激活函数说明2.1 Sigmoid2.1.1 公式2.1.2 图像2.1.3 代码解读 2.2 Softmax2.2.1 公式2.2.2 代码解读 2.3 EL…
阅读更多...
A.深度学习基础入门篇[四]：激活函数介绍:tanh、sigmoid、ReLU、PReLU、ELU、softplus、softmax、swish等

A.深度学习基础入门篇[四]：激活函数介绍:tanh、sigmoid、ReLU、PReLU、ELU、softplus、softmax、swish等

【深度学习入门到进阶】必看系列，含激活函数、优化策略、损失函数、模型调优、归一化算法、卷积模型、序列模型、预训练模型、对抗神经网络等 专栏详细介绍：【深度学习入门到进阶】必看系列，含激活函数、优化策略、损失函数、模型调优、归一化…
阅读更多...
el-descriptions

el-descriptions

<el-descriptions title"用户信息"><el-descriptions-item label"用户名">kooriookami</el-descriptions-item><el-descriptions-item label"手机号">18100000000</el-descriptions-item><el-descriptions-ite…
阅读更多...
功能性模块：（8）一文理解常用激活函数（Sigmoid，ReLU，ELU，GELU...）

功能性模块：（8）一文理解常用激活函数（Sigmoid，ReLU，ELU，GELU...）

一文理解常用激活函数 1. Sigmoid 公式&#xff1a; Sigmoid ( x ) 1 1 exp ⁡ ( − x ) \text{Sigmoid}(x) \frac{1}{1 \exp(-x)} Sigmoid(x)1exp(−x)1​ Sigmoid的函数形状如下图所示: 对应的导数形式如下图所示&#xff1a; Sigmoid函数的优点&#xff1a; 便于求…
阅读更多...
深入理解ReLU、Leaky ReLU、 PReLU、ELU、Softplus

深入理解ReLU、Leaky ReLU、 PReLU、ELU、Softplus

文章目录 ReLULeaky ReLUPReLUELUSoftplus ReLU ReLU&#xff08;Rectified Linear Unit&#xff0c;修正线性单元&#xff09;&#xff0c;也叫Rectifier 函数&#xff0c;它的定义如下&#xff1a; Relu可以实现单侧抑制&#xff08;即把一部分神经元置0&#xff09;&#x…
阅读更多...
搞懂激活函数(Sigmoid/ReLU/LeakyReLU/PReLU/ELU)

搞懂激活函数(Sigmoid/ReLU/LeakyReLU/PReLU/ELU)

1. 简介 在深度学习中&#xff0c;输入值和矩阵的运算是线性的&#xff0c;而多个线性函数的组合仍然是线性函数&#xff0c;对于多个隐藏层的神经网络&#xff0c;如果每一层都是线性函数&#xff0c;那么这些层在做的就只是进行线性计算&#xff0c;最终效果和一个隐藏层相当…
阅读更多...
YOLOv5改进系列（13）——更换激活函数之SiLU，ReLU，ELU，Hardswish，Mish，Softplus，AconC系列等

YOLOv5改进系列（13）——更换激活函数之SiLU，ReLU，ELU，Hardswish，Mish，Softplus，AconC系列等

【YOLOv5改进系列】前期回顾： YOLOv5改进系列（0）——重要性能指标与训练结果评价及分析 YOLOv5改进系列（1）——添加SE注意力机制
阅读更多...
【PyTorch】教程：torch.nn.ELU

【PyTorch】教程：torch.nn.ELU

torch.nn.ELU CLASS torch.nn.ELU(alpha1.0, inplaceFalse) paper: Fast and Accurate Deep Network Learning by Exponential Linear Units (ELUs). 参数 alpha ([float]) – α \alpha α 默认为1.0inplace ([bool] ) – 内部做, 默认为 False ELU 定义 ELU ( x ) { x , …
阅读更多...
【YOLOv7/YOLOv5系列算法改进NO.54】改进激活函数为ReLU、RReLU、Hardtanh、ReLU6、Sigmoid、Tanh、Mish、Hardswish、ELU、CELU等

【YOLOv7/YOLOv5系列算法改进NO.54】改进激活函数为ReLU、RReLU、Hardtanh、ReLU6、Sigmoid、Tanh、Mish、Hardswish、ELU、CELU等

文章目录 前言一、解决问题二、基本原理三、​添加方法四、总结 前言 作为当前先进的深度学习目标检测算法YOLOv7&#xff0c;已经集合了大量的trick&#xff0c;但是还是有提高和改进的空间&#xff0c;针对具体应用场景下的检测难点&#xff0c;可以不同的改进方法。此后的系…
阅读更多...
常用激活函数：Sigmoid、Tanh、Relu、Leaky Relu、ELU优缺点总结

常用激活函数：Sigmoid、Tanh、Relu、Leaky Relu、ELU优缺点总结

1、激活函数的作用 什么是激活函数&#xff1f; 在神经网络中&#xff0c;输入经过权值加权计算并求和之后&#xff0c;需要经过一个函数的作用&#xff0c;这个函数就是激活函数&#xff08;Activation Function&#xff09;。 激活函数的作用&#xff1f; 首先我们需要知道…
阅读更多...
深度学习—激活函数详解（Sigmoid、tanh、ReLU、ReLU6及变体P-R-Leaky、ELU、SELU、Swish、Mish、Maxout、hard-sigmoid、hard-swish）

深度学习—激活函数详解（Sigmoid、tanh、ReLU、ReLU6及变体P-R-Leaky、ELU、SELU、Swish、Mish、Maxout、hard-sigmoid、hard-swish）

非线性激活函数详解 饱和激活函数Sigmoid函数tanh函数hard-Sigmoid函数 非饱和激活函数Relu&#xff08;修正线性单元&#xff09;&#xff1a;Relu6&#xff08;抑制其最大值&#xff09;&#xff1a;ELU&#xff08;指数线性单元&#xff09;SELULeaky-Relu / R-ReluP-Relu&a…
阅读更多...
激活函数详解（ReLU/Leaky ReLU/ELU/SELU/Swish/Maxout/Sigmoid/tanh）

激活函数详解（ReLU/Leaky ReLU/ELU/SELU/Swish/Maxout/Sigmoid/tanh）

神经网络中使用激活函数来加入非线性因素&#xff0c;提高模型的表达能力。 ReLU(Rectified Linear Unit,修正线性单元) 形式如下: ReLU公式近似推导:: 下面解释上述公式中的softplus,Noisy ReLU. softplus函数与ReLU函数接近,但比较平滑, 同ReLU一样是单边抑制,有宽广的接受…
阅读更多...
【卷积神经网络】12、激活函数 | Tanh / Sigmoid / ReLU / Leaky ReLU / ELU / SiLU / Mish

【卷积神经网络】12、激活函数 | Tanh / Sigmoid / ReLU / Leaky ReLU / ELU / SiLU / Mish

文章目录 一、Tanh二、Sigmoid三、ReLU四、Leaky ReLU五、ELU六、SiLU七、Mish 本文主要介绍卷积神经网络中常用的激活函数及其各自的优缺点 最简单的激活函数被称为线性激活&#xff0c;其中没有应用任何转换。 一个仅由线性激活函数组成的网络很容易训练&#xff0c;但不能学…
阅读更多...
神经网络激活函数汇总（Sigmoid、tanh、ReLU、LeakyReLU、pReLU、ELU、maxout）

神经网络激活函数汇总（Sigmoid、tanh、ReLU、LeakyReLU、pReLU、ELU、maxout）

神经网络激活函数汇总&#xff08;Sigmoid、tanh、ReLU、LeakyReLU、pReLU、ELU、maxout&#xff09; 常规 sigmoid 和 tanh sigmoid 特点&#xff1a;可以解释&#xff0c;比如将0-1之间的取值解释成一个神经元的激活率&#xff08;firing rate&#xff09; 缺陷&#xff1…
阅读更多...
神经网络激活函数优缺点和比较（sigmod，tanh，relu，softmax，leaky relu，ELU,SELU）

神经网络激活函数优缺点和比较（sigmod，tanh，relu，softmax，leaky relu，ELU,SELU）

文章目录 前言一、sigmoid函数二、tanh函数三&#xff0c;ReLU函数四&#xff0c; Leaky ReLU五&#xff0c;ELU指数线性单元函数&SELU函数六&#xff0c;softmax函数 前言 理想的激活函数应该有的性质 非线性&#xff1a;这个条件是多层神经网络形成的基础&#xff0c;保…
阅读更多...
常用激活函数：Sigmoid/Softmax/ELU/ReLU/LeakyReLU/Tanh...（Pytorch）

常用激活函数：Sigmoid/Softmax/ELU/ReLU/LeakyReLU/Tanh...（Pytorch）

激活函数 一、Sigmoid1.介绍2.实例 二、Softmax1.介绍2.实例 三、ELU&#xff1a;指数线性单元函数1.介绍2.实例 四、ReLU&#xff1a;整流线性单元函数1.介绍2.实例 五、ReLU61.介绍2.实例 六、LeakyReLU1.介绍2.实例 七、Tanh&#xff1a;双曲正切函数1.介绍2.实例 一、Sigmo…
阅读更多...
【深度学习】论文导读：ELU激活函数的提出（FAST AND ACCURATE DEEP NETWORK LEARNING BY EXPONENTIAL LINEAR UNITS (ELUS)）

【深度学习】论文导读：ELU激活函数的提出（FAST AND ACCURATE DEEP NETWORK LEARNING BY EXPONENTIAL LINEAR UNITS (ELUS)）

论文下载&#xff1a; FAST AND ACCURATE DEEP NETWORK LEARNING BY EXPONENTIAL LINEAR UNITS (ELUS)&#xff08;2016&#xff0c;Djork-Arne Clevert, Thomas Unterthiner & Sepp Hochreiter&#xff09; 一、简介 ELU的表达式&#xff1a; 四种激活函数&#xff0…
阅读更多...
推荐文章

Copyright @ 2022~2023