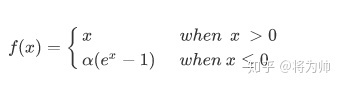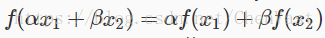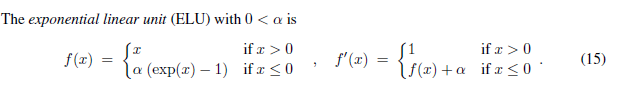【深度学习入门到进阶】必看系列,含激活函数、优化策略、损失函数、模型调优、归一化算法、卷积模型、序列模型、预训练模型、对抗神经网络等

专栏详细介绍:【深度学习入门到进阶】必看系列,含激活函数、优化策略、损失函数、模型调优、归一化算法、卷积模型、序列模型、预训练模型、对抗神经网络等
本专栏主要方便入门同学快速掌握相关知识。声明:部分项目为网络经典项目方便大家快速学习,后续会不断增添实战环节(比赛、论文、现实应用等)
专栏订阅:深度学习入门到进阶专栏
1.激活函数
-
激活函数是人工神经网络的一个极其重要的特征;
-
激活函数决定一个神经元是否应该被激活,激活代表神经元接收的信息与给定的信息有关;
-
激活函数对输入信息进行非线性变换,然后将变换后的输出信息作为输入信息传给下一层神经元。
激活函数的作用
如果不用激活函数,每一层输出都是上层输入的线性函数,无论神经网络有多少层,最终的输出都是输入的线性组合。 激活函数给神经元引入了非线性因素,使得神经网络可以任意逼近任何非线性函数。
2.常见激活函数种类介绍
2.1 sigmoid
函数定义:
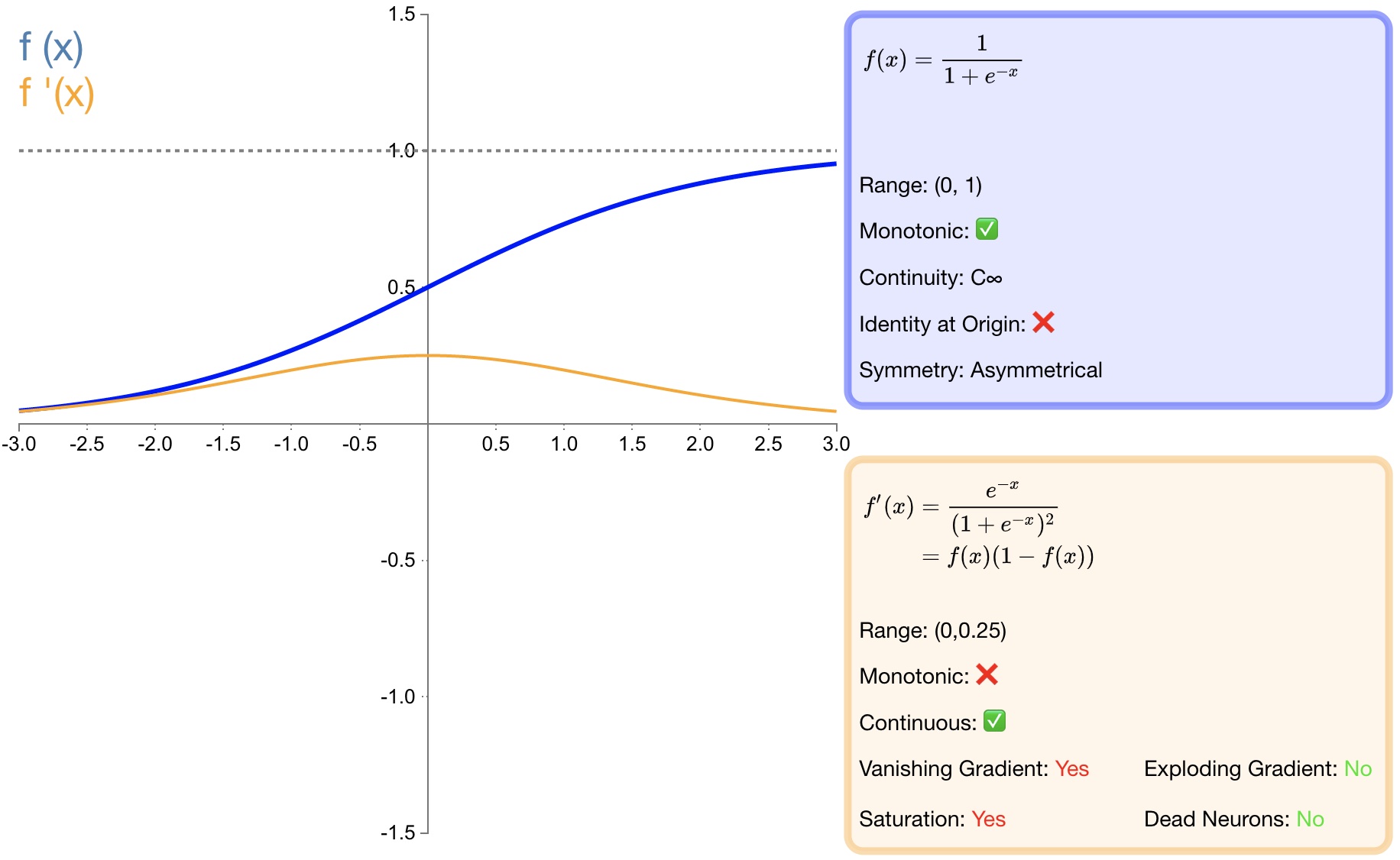
f ( x ) = σ ( x ) = 1 1 + e − x f(x)=\sigma(x)=\dfrac{1}{1+e^{-x}}\quad\text{} f(x)=σ(x)=1+e−x1
导数:
f ′ ( x ) = f ( x ) ( 1 − f ( x ) ) f^{'}(x)=f(x)(1-f(x)) f′(x)=f(x)(1−f(x))
-
优点:
-
s i g m o i d sigmoid sigmoid函数的输出映射在 (0,1)之间,单调连续,输出范围有限,优化稳定,可以用作输出层;
-
求导容易;
-
-
缺点:
-
由于其软饱和性,一旦落入饱和区梯度就会接近于0,根据反向传播的链式法则,容易产生梯度消失,导致训练出现问题;
-
Sigmoid函数的输出恒大于0。非零中心化的输出会使得其后一层的神经元的输入发生偏置偏移(Bias Shift),并进一步使得梯度下降的收敛速度变慢;
-
计算时,由于具有幂运算,计算复杂度较高,运算速度较慢。
-
2.2 tanh
函数定义:
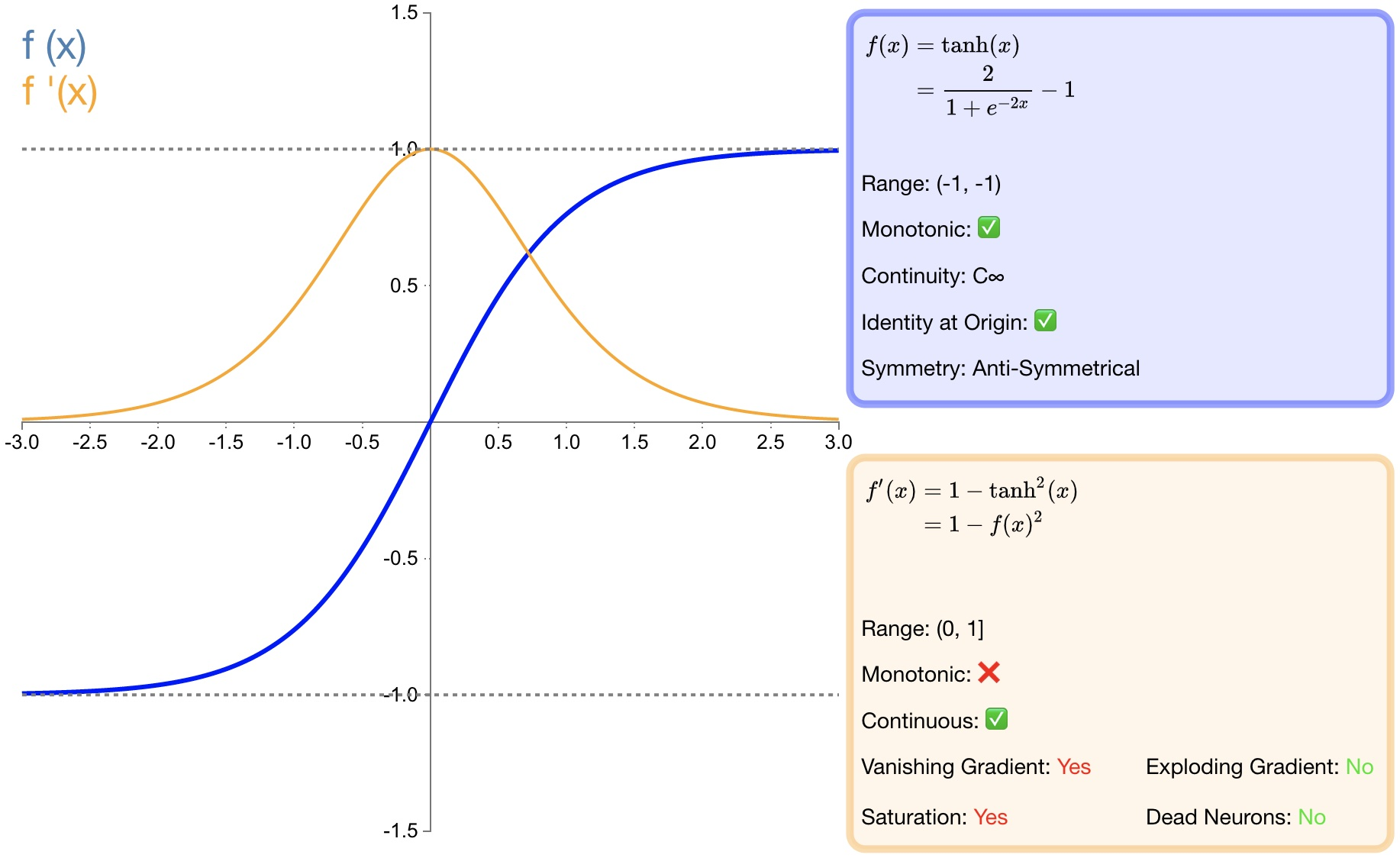
f ( x ) = tanh ( x ) = e x − e − x e x + e − x f(x)=\tanh (x)=\frac{e^x-e^{-x}}{e^x+e^{-x}} f(x)=tanh(x)=ex+e−xex−e−x
导数:
f ′ ( x ) = 1 − f ( x ) 2 f^{'}(x)=1-f(x)^2 f′(x)=1−f(x)2
-
优点:
-
tanh比 sigmoid函数收敛速度更快;
-
相比 sigmoid函数,tanh是以 0为中心的;
-
-
缺点:
-
与 sigmoid函数相同,由于饱和性容易产生的梯度消失;
-
与 sigmoid函数相同,由于具有幂运算,计算复杂度较高,运算速度较慢。
-
2.3 ReLU
函数定义:
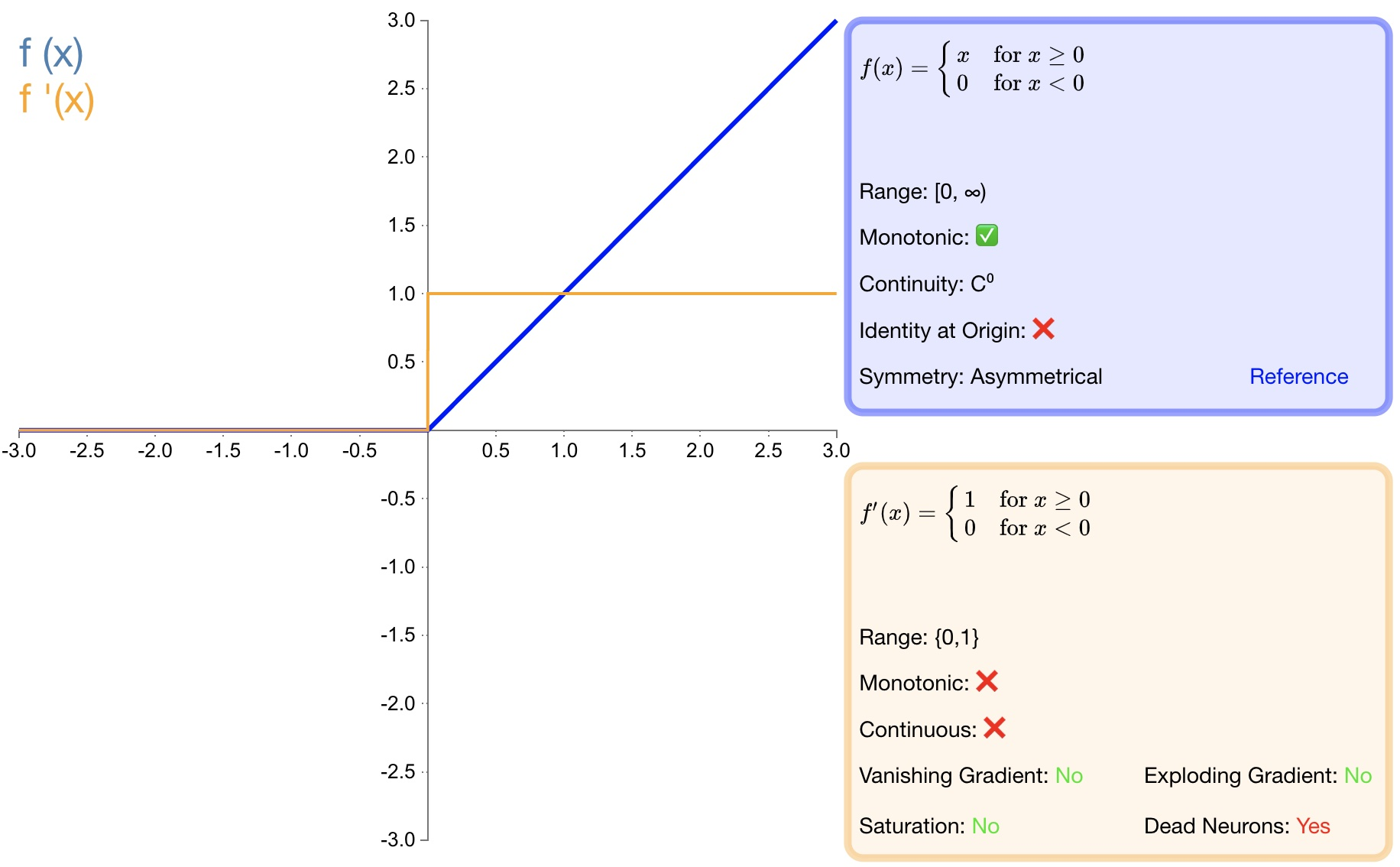
f ( x ) = { 0 x < 0 x x ≥ 0 f(x)=\left\{\begin{array}{lr}0&x<0\\ x&x\geq0\end{array}\right. f(x)={0xx<0x≥0
导数:
f ( x ) ′ = { 0 x < 0 1 x ≥ 0 f(x)^{\prime}= \begin{cases}0 & x<0 \\ 1 & x \geq 0\end{cases} f(x)′={01x<0x≥0
-
优点:
-
收敛速度快;
-
相较于 sigmoid和 tanh中涉及了幂运算,导致计算复杂度高, ReLU可以更加简单的实现;
-
当输入 x>=0时,ReLU 的导数为常数,这样可有效缓解梯度消失问题;
-
当 x<0时,ReLU 的梯度总是 0,提供了神经网络的稀疏表达能力;
-
-
缺点:
-
ReLU 的输出不是以 0为中心的;
-
神经元坏死现象,某些神经元可能永远不会被激活,导致相应参数永远不会被更新;
-
不能避免梯度爆炸问题;
-
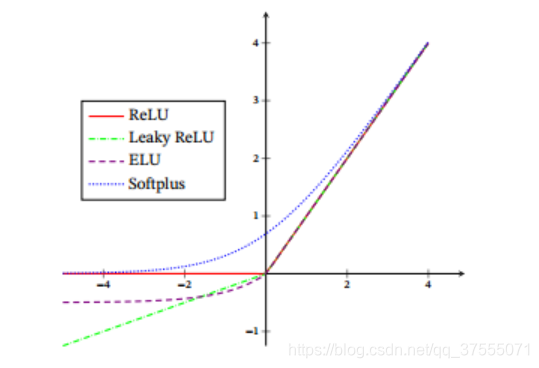
2.4 LReLU
函数定义:
f ( x ) = { α x x < 0 x x ≥ 0 f(x)=\left\{\begin{array}{lr}\alpha x&x<0\\ x&x\geq0\end{array}\right.\quad f(x)={αxxx<0x≥0
导数:
f ( x ) ′ = { α x < 0 1 x ≥ 0 f(x)^{'}=\begin{cases}\alpha&x<0\\ 1&x\geq0\end{cases} f(x)′={α1x<0x≥0

-
优点:
-
避免梯度消失;
-
由于导数总是不为零,因此可减少死神经元的出现;
-
-
缺点:
-
LReLU 表现并不一定比 ReLU 好;
-
无法避免梯度爆炸问题;
-
2.5 PReLU
函数定义 :
f ( α , x ) = { α x x < 0 x x ≥ 0 f(\alpha,x)=\left\{\begin{array}{lr}\alpha x&x<0\\ x&x\geq0\end{array}\right.\quad f(α,x)={αxxx<0x≥0
导数:
f ( α , x ) ′ = { α x < 0 1 x ≥ 0 f\left(\alpha,x\right)'=\left\{\begin{array}{cc}\alpha&x<0\\ 1&x\ge0\end{array}\right.\quad f(α,x)′={α1x<0x≥0
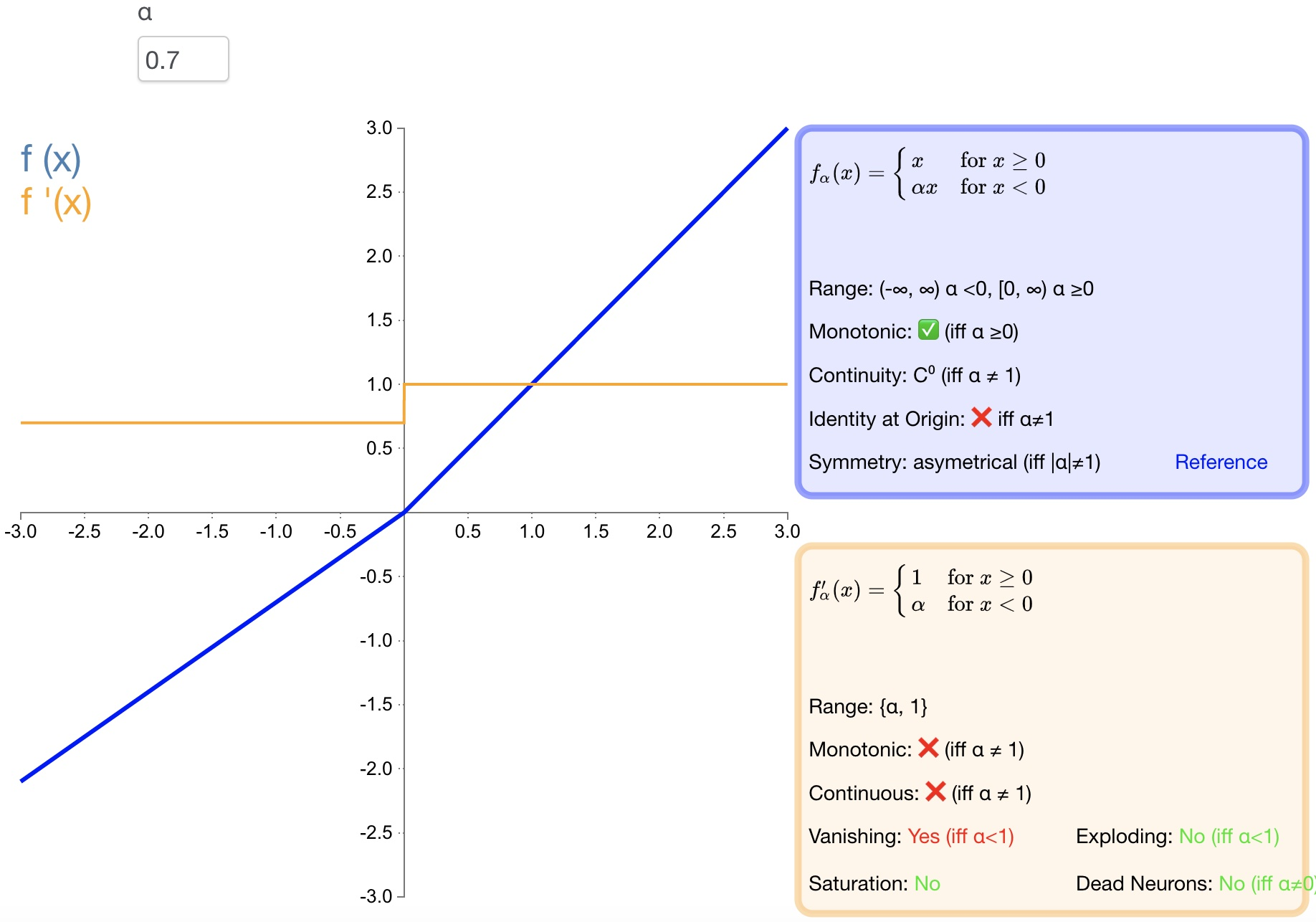
-
优点:
-
PReLU 是 LReLU 的改进,可以自适应地从数据中学习参数;
-
收敛速度快、错误率低;
-
PReLU 可以用于反向传播的训练,可以与其他层同时优化;
-
2.6 RReLU
函数定义:
f ( α , x ) = { α x x < 0 x x ≥ 0 f(\alpha,x)=\left\{\begin{array}{lr}\alpha x&x<0\\ x&x\geq0\end{array}\right. f(α,x)={αxxx<0x≥0
导数:
f ( α , x ) ′ = { α x < 0 1 x ≥ 0 f(\alpha,x)'=\left\{\begin{array}{lr}\alpha&x<0\\ 1&x\geq0\end{array}\right. f(α,x)′={α1x<0x≥0
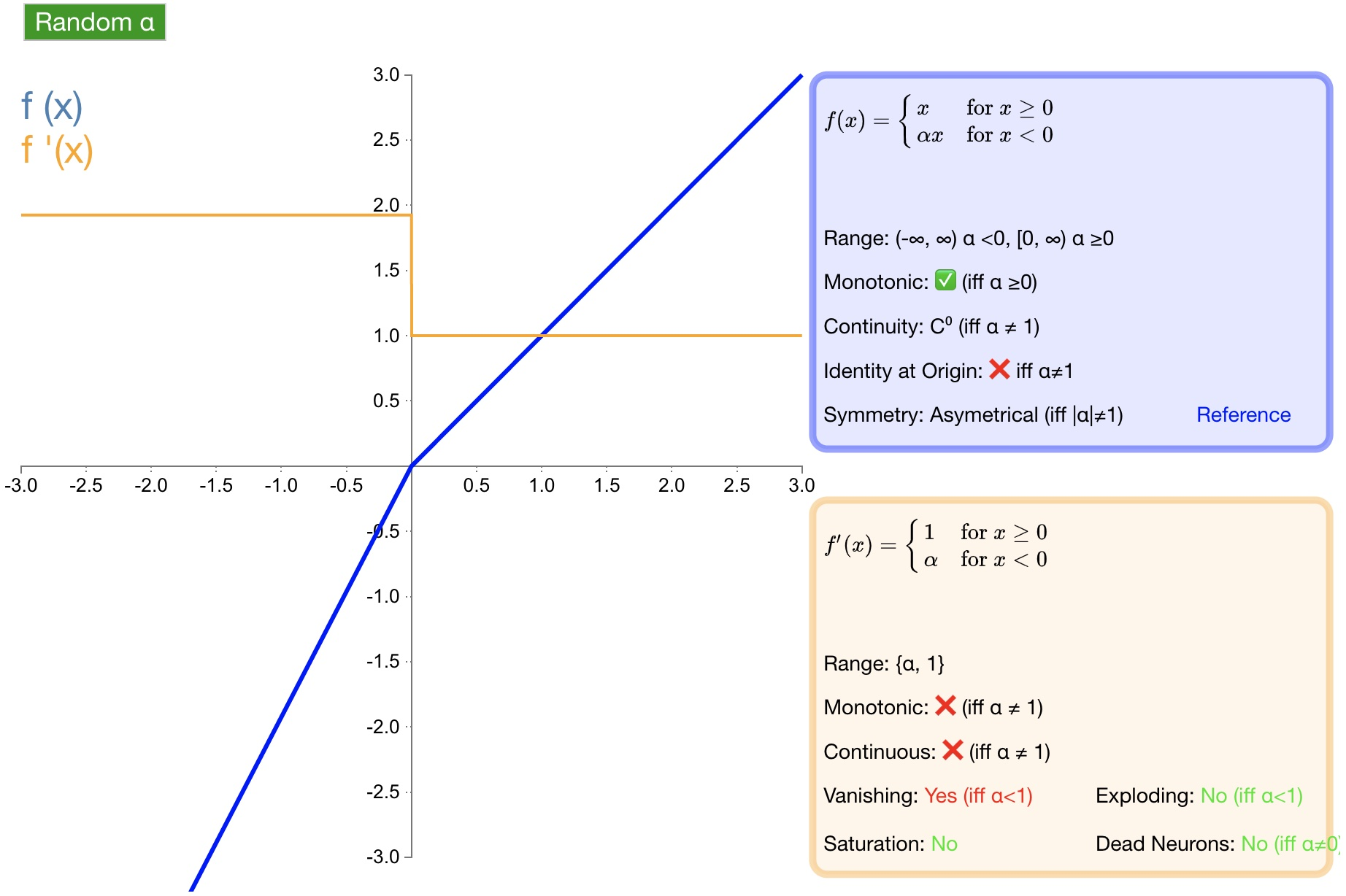
优点:为负值输入添加了一个线性项,这个线性项的斜率在每一个节点上都是随机分配的(通常服从均匀分布)。
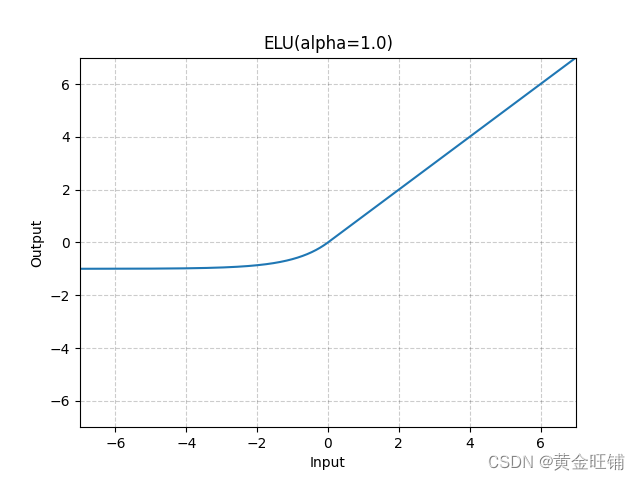
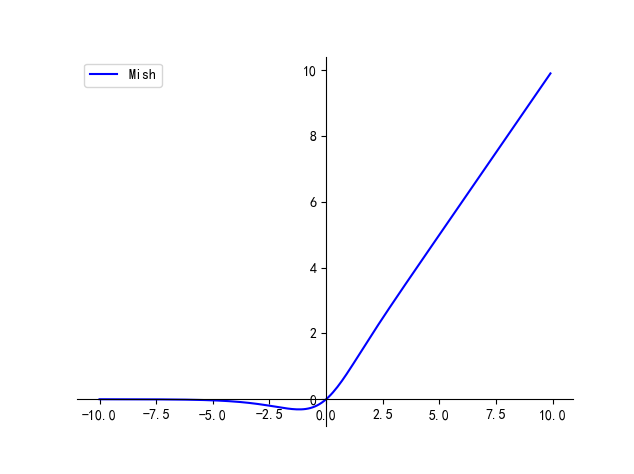
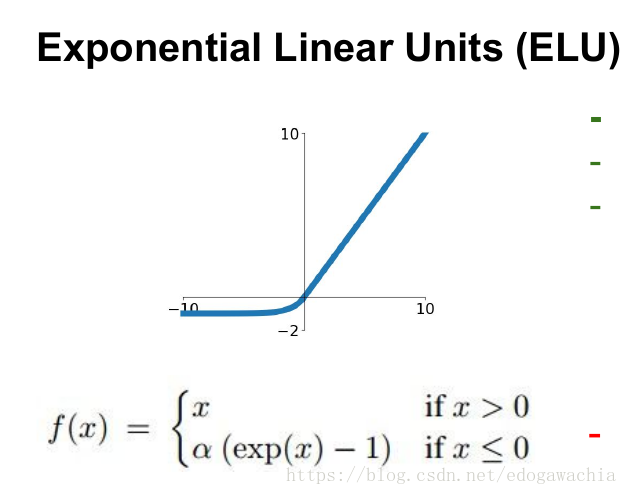
2.7 ELU
函数定义:
f ( α , x ) = { α ( e x − 1 ) x < 0 x x ≥ 0 f(\alpha,x)=\left\{\begin{array}{lr}\alpha\left(e^x-1\right)&x<0\\ x&x\ge0\end{array}\right. f(α,x)={α(ex−1)xx<0x≥0
导数:
f ( α , x ) ′ = { f ( α , x ) + α x < 0 1 x ≥ 0 f(\alpha,x)^{'}=\left\{\begin{array}{lr}f(\alpha,x)+\alpha&x<0\\ 1&x\geq0\end{array}\right. f(α,x)′={f(α,x)+α1x<0x≥0
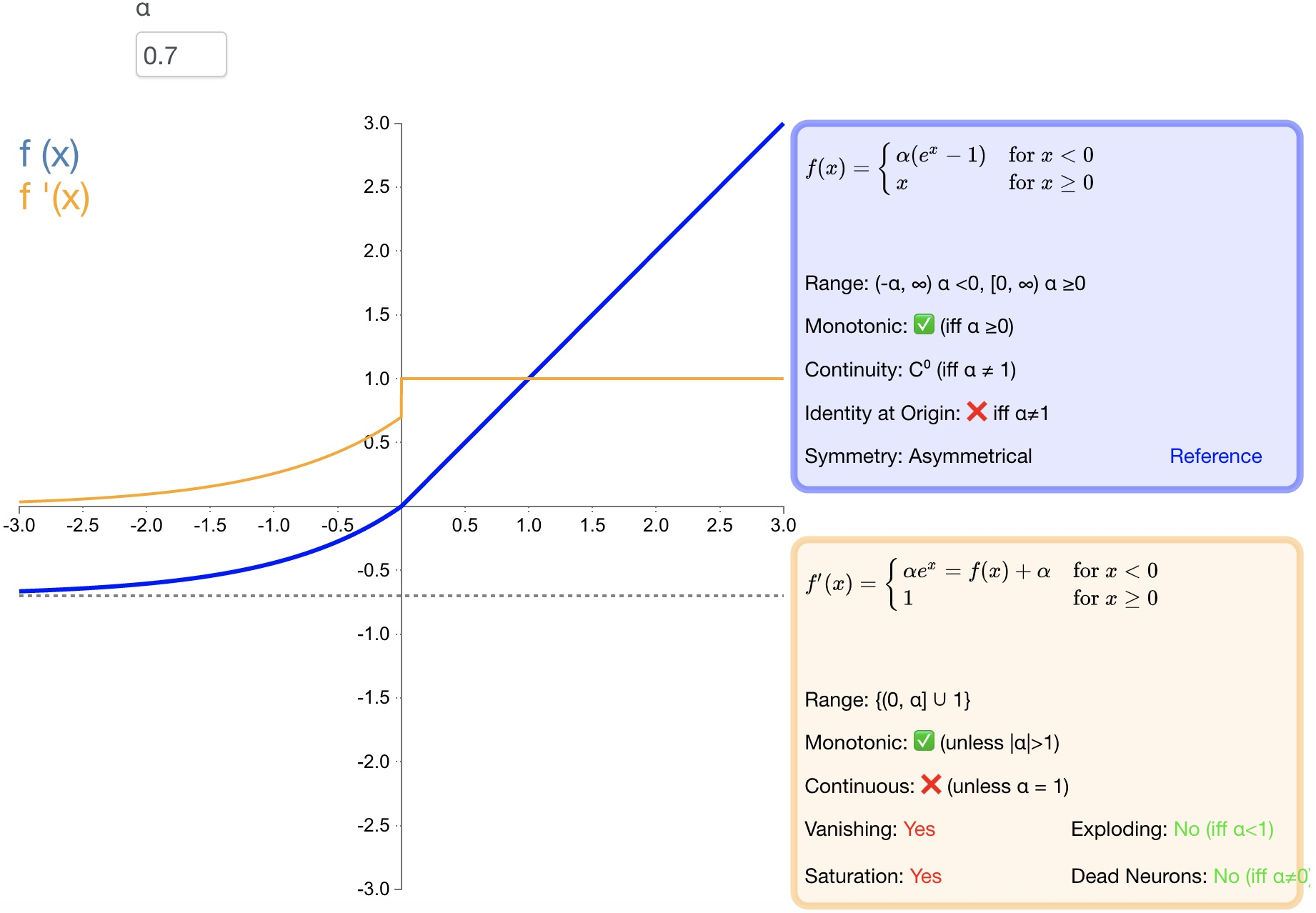
-
优点:
-
导数收敛为零,从而提高学习效率;
-
能得到负值输出,这能帮助网络向正确的方向推动权重和偏置变化;
-
防止死神经元出现。
-
-
缺点:
-
计算量大,其表现并不一定比 ReLU 好;
-
无法避免梯度爆炸问题;
-
2.8 SELU
函数定义:
f ( α , x ) = λ { α ( e x − 1 ) x < 0 x x ≥ 0 f(\alpha,x)=\lambda\left\{\begin{array}{lr}\alpha\left(e^x-1\right)&x<0\\ x&x\geq0\end{array}\right. f(α,x)=λ{α(ex−1)xx<0x≥0
导数:
f ( α , x ) ′ = λ { α ( e x ) x < 0 1 x ≥ 0 f(\alpha,x)'=\lambda\left\{\begin{array}{lr}\alpha\left(e^x\right)&x<0\\ 1&x\geq0\end{array}\right. f(α,x)′=λ{α(ex)1x<0x≥0
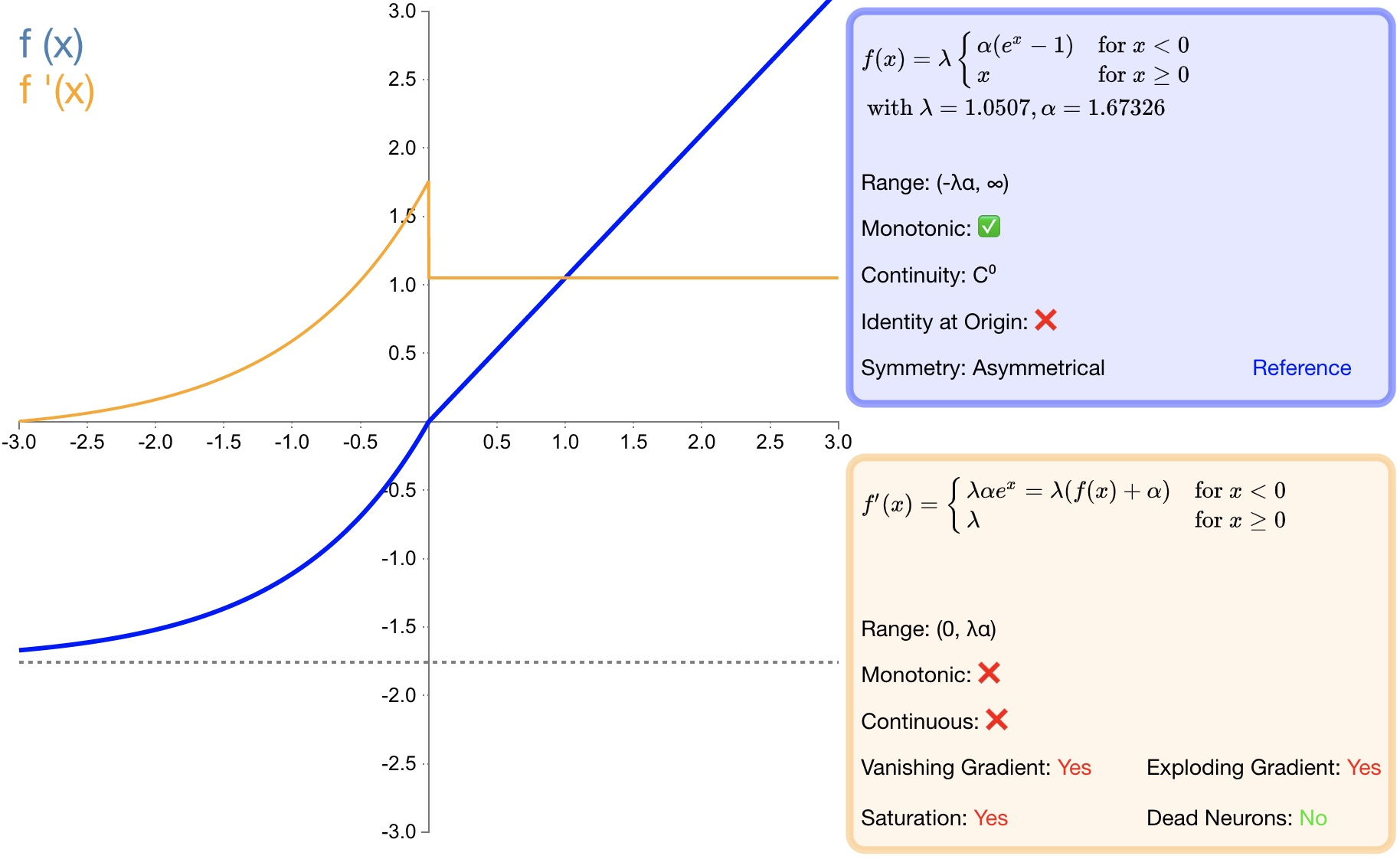
-
优点:
-
SELU 是 ELU 的一个变种。其中 λ 和 α 是固定数值(分别为 1.0507和 1.6726);
-
经过该激活函数后使得样本分布自动归一化到 0均值和单位方差;
-
不会出现梯度消失或爆炸问题;
-
2.9 softsign
函数定义:
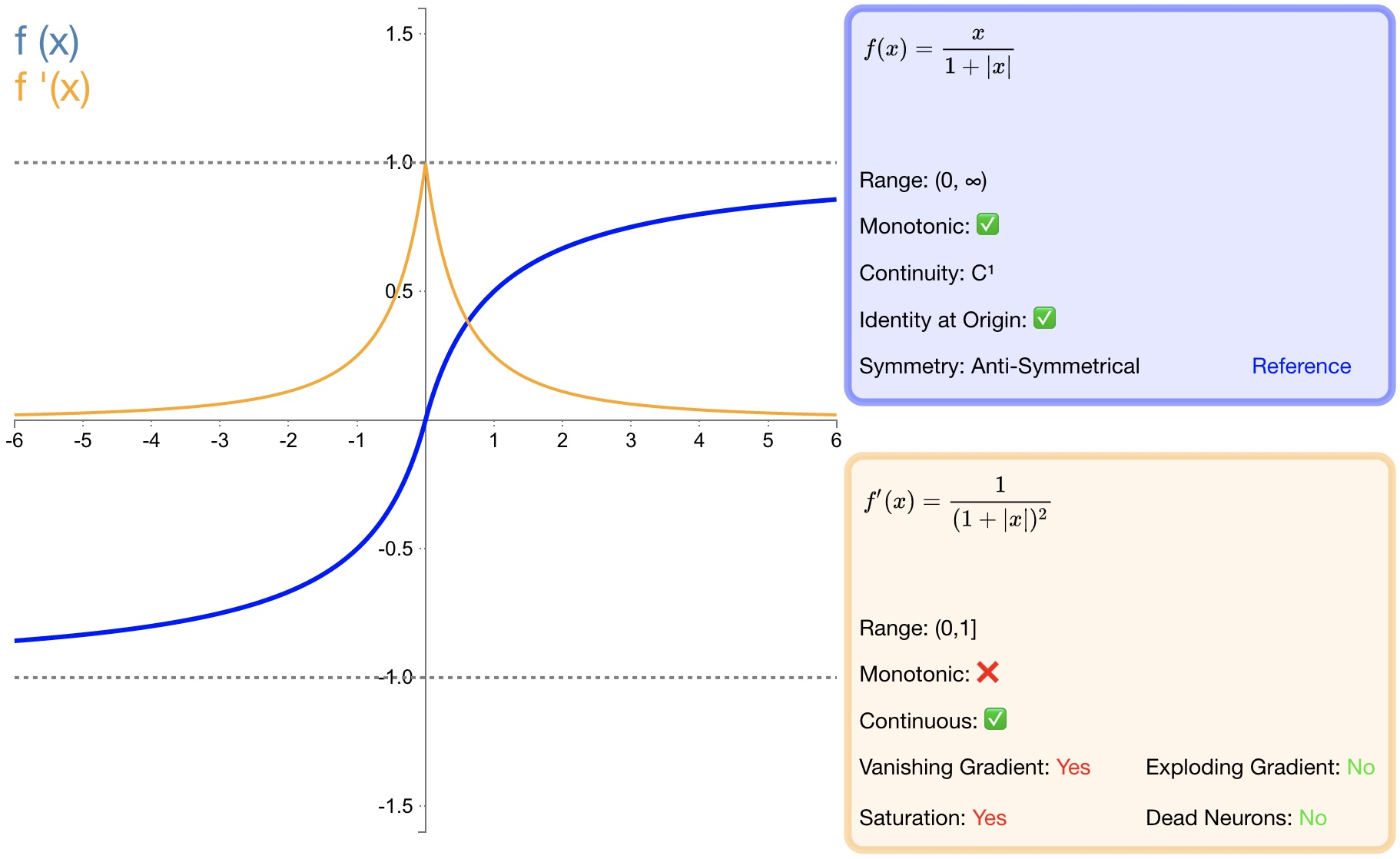
f ( x ) = x ∣ x ∣ + 1 f(x)=\dfrac{x}{|x|+1}\quad\text{} f(x)=∣x∣+1x
导数:
f ′ ( x ) = 1 ( 1 + ∣ x ∣ ) 2 f'(x)=\frac{1}{\left(1+\left|x\right|\right)^2}\quad\text{} f′(x)=(1+∣x∣)21
-
优点:
-
softsign是 tanh激活函数的另一个替代选择;
-
softsign是反对称、去中心、可微分,并返回 −1和 1之间的值;
-
softsign更平坦的曲线与更慢的下降导数表明它可以更高效地学习;
-
-
缺点:
- 导数的计算比tanh更麻烦;
2.10 softplus
函数定义:
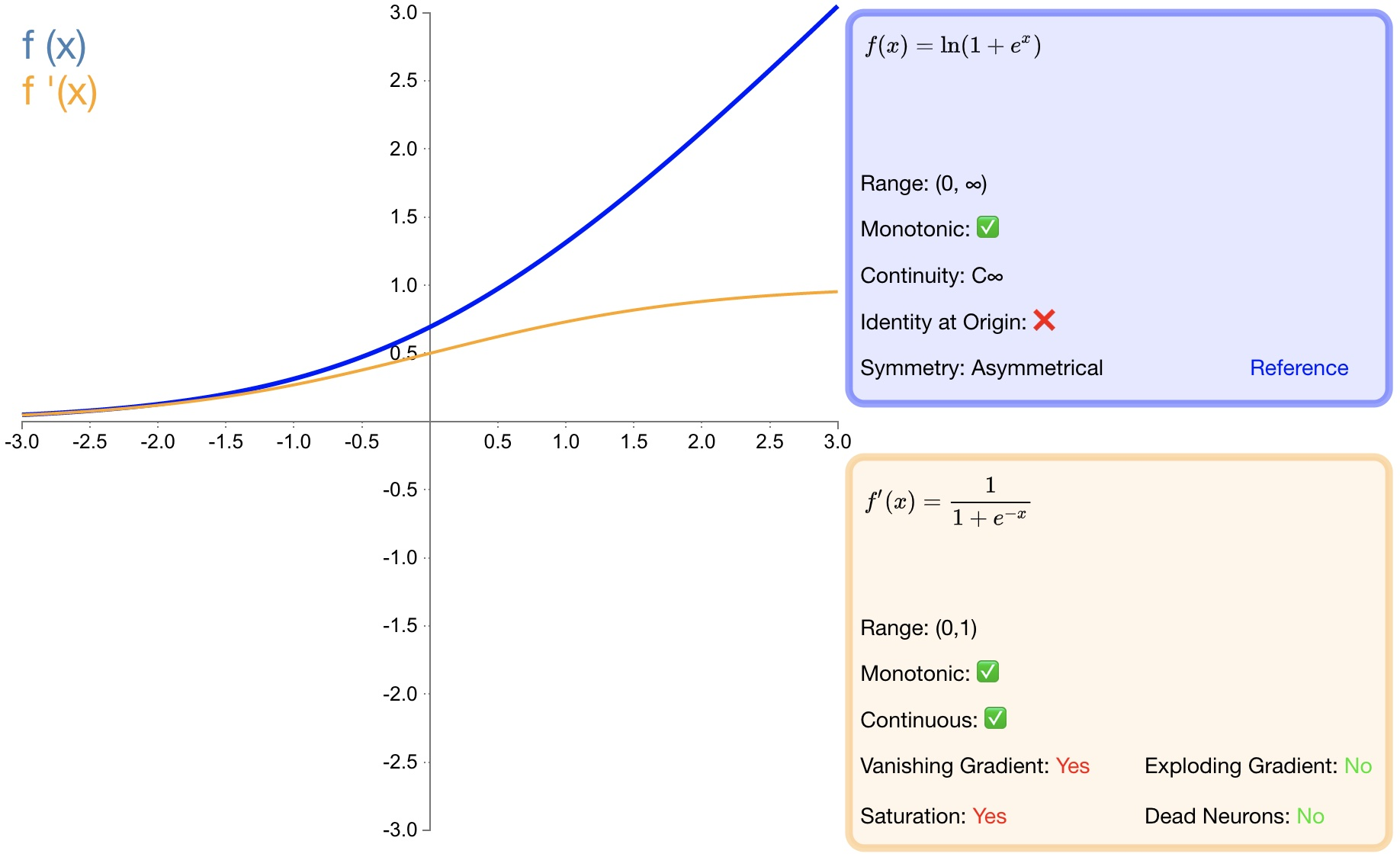
f ( x ) = ln ( 1 + e x ) f(x)=\ln\left(1+e^x\right)\quad\quad f(x)=ln(1+ex)
导数:
f ′ ( x ) = 1 1 + e − x f'(x)=\dfrac{1}{1+e^{-x}} f′(x)=1+e−x1
-
优点:
-
作为 relu 的一个不错的替代选择,softplus能够返回任何大于 0的值。
-
与 relu不同,softplus的导数是连续的、非零的,无处不在,从而防止出现死神经元。
-
-
缺点:
-
导数常常小于 1,也可能出现梯度消失的问题。
-
softplus另一个不同于 relu的地方在于其不对称性,不以零为中心,可能会妨碍学习。
-
3.多分类激活函数
3.1 softmax
softmax 函数一般用于多分类问题中,它是对逻辑斯蒂(logistic)回归的一种推广,也被称为多项逻辑斯蒂回归模型(multi-nominal logistic mode)。假设要实现 k 个类别的分类任务,Softmax 函数将输入数据 xi映射到第 i个类别的概率 yi如下计算:
y i = s o f t w a r e max ( x i ) = e x i ∑ j = 1 k e x j y_i=software\max\left(x_i\right)=\dfrac{e^{x_i}}{\sum_{j=1}^{k}e^{x_j}} yi=softwaremax(xi)=∑j=1kexjexi
显然, 0 < y i < 1 0<yi<1 0<yi<1。图13 给出了三类分类问题的 softmax 输出示意图。在图中,对于取值为 4、1和-4 的 x1、x2和 x3,通过 softmax 变换后,将其映射到 (0,1) 之间的概率值。
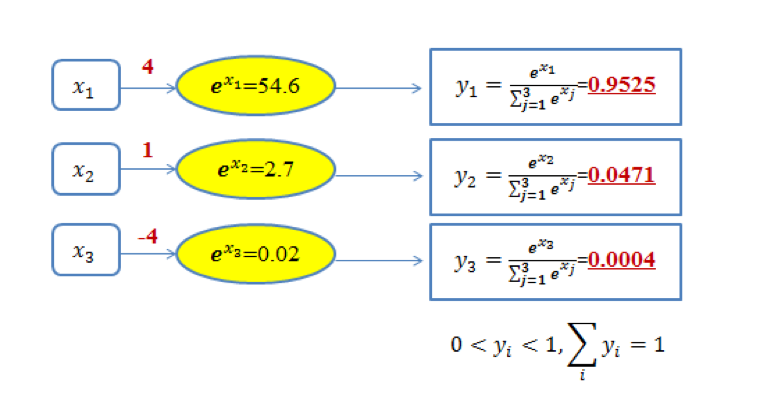
由于 softmax 输出结果的值累加起来为 1,因此可将输出概率最大的作为分类目标(图 1 中被分类为第一类)。
也可以从如下另外一个角度来理解图 1 中的内容:给定某个输入数据,可得到其分类为三个类别的初始结果,分别用 x1、x2和 x3来表示。这三个初始分类结果分别是 4、1和-4。通过 Softmax 函数,得到了三个类别分类任务中以概率表示的更好的分类结果,即分别以 95.25%、4.71%和0.04% 归属于类别1、类别2 和类别3。显然,基于这样的概率值,可判断输入数据属于第一类。可见,通过使用 Softmax 函数,可求取输入数据在所有类别上的概率分布。
3.2 swish
函数定义:
f ( x ) = x ⋅ σ ( x ) f(x)=x\cdot\sigma(x) f(x)=x⋅σ(x)
其中,σ是 sigmoid函数。
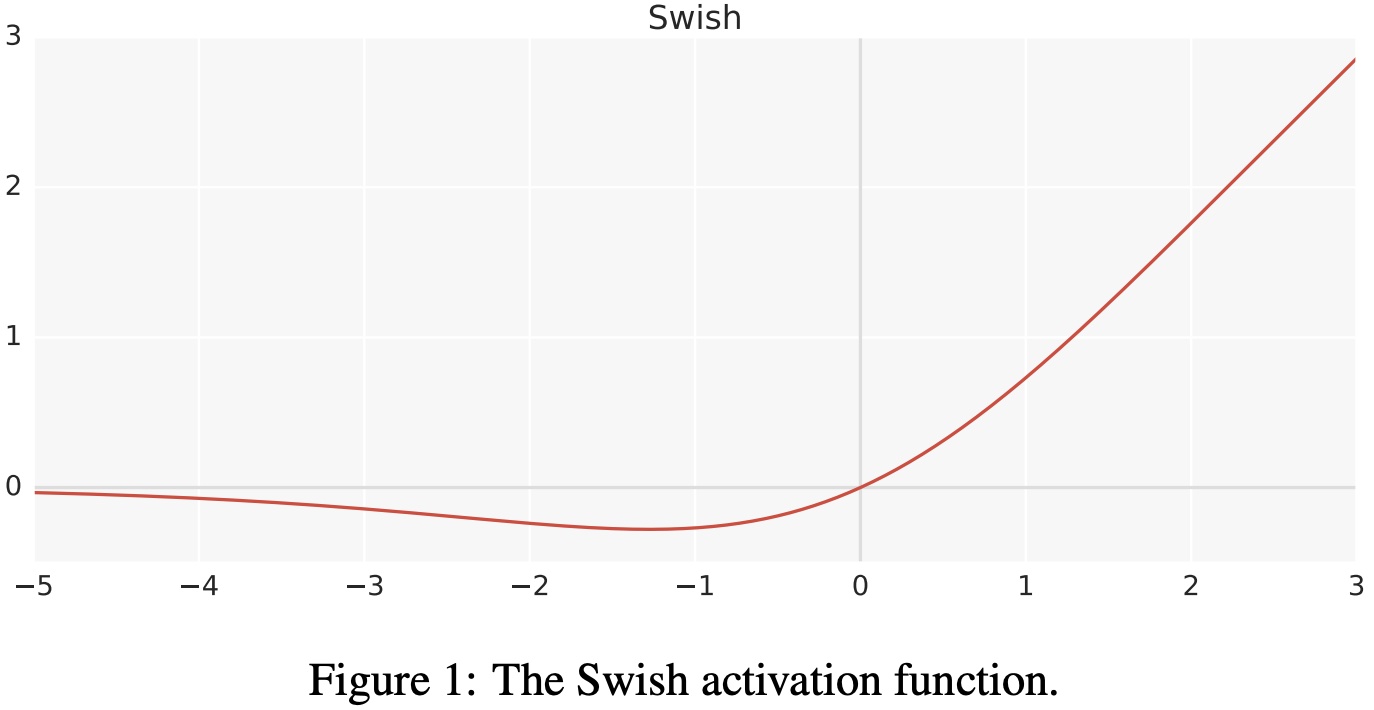
- swish激活函数的一阶导数如下
f ′ ( x ) = σ ( x ) + x ⋅ σ ( x ) ( 1 − σ ( x ) ) = σ ( x ) + x ⋅ σ ( x ) − x ⋅ σ ( x ) 2 = x ⋅ σ ( x ) + σ ( x ) ( 1 − x ⋅ σ ( x ) ) = f ( x ) + σ ( x ) ( 1 − f ( x ) ) \begin{aligned}f'\left(x\right)=\sigma\left(x\right)+x\cdot\sigma\left(x\right)\left(1-\sigma\left(x\right)\right)\\ =\sigma\left(x\right)+x\cdot\sigma\left(x\right)-x\cdot\sigma\left(x\right)^2\\ =x\cdot\sigma\left(x\right)+\sigma\left(x\right)\left(1-x\cdot\sigma\left(x\right)\right)\\ =f\left(x\right)+\sigma\left(x\right)\left(1-f\left(x\right)\right)\end{aligned} f′(x)=σ(x)+x⋅σ(x)(1−σ(x))=σ(x)+x⋅σ(x)−x⋅σ(x)2=x⋅σ(x)+σ(x)(1−x⋅σ(x))=f(x)+σ(x)(1−f(x))
- swish激活函数的一阶和二阶导数的图形如
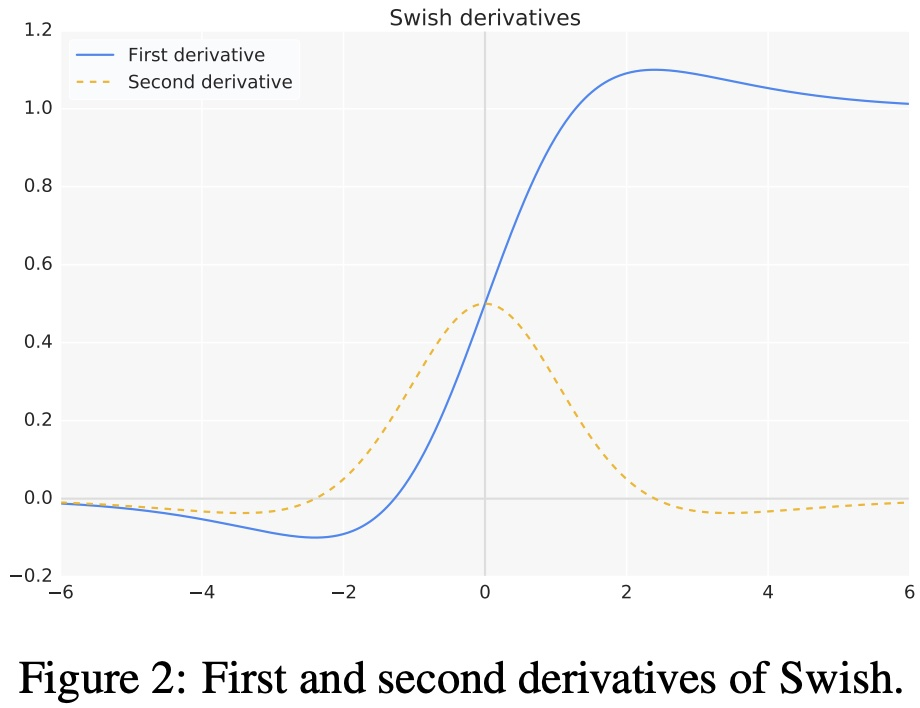
- 超参数版 swish激活函数:
f ( x ) = x ⋅ σ ( β x ) f\left(x\right)=x\cdot\sigma\left(\beta x\right) f(x)=x⋅σ(βx)
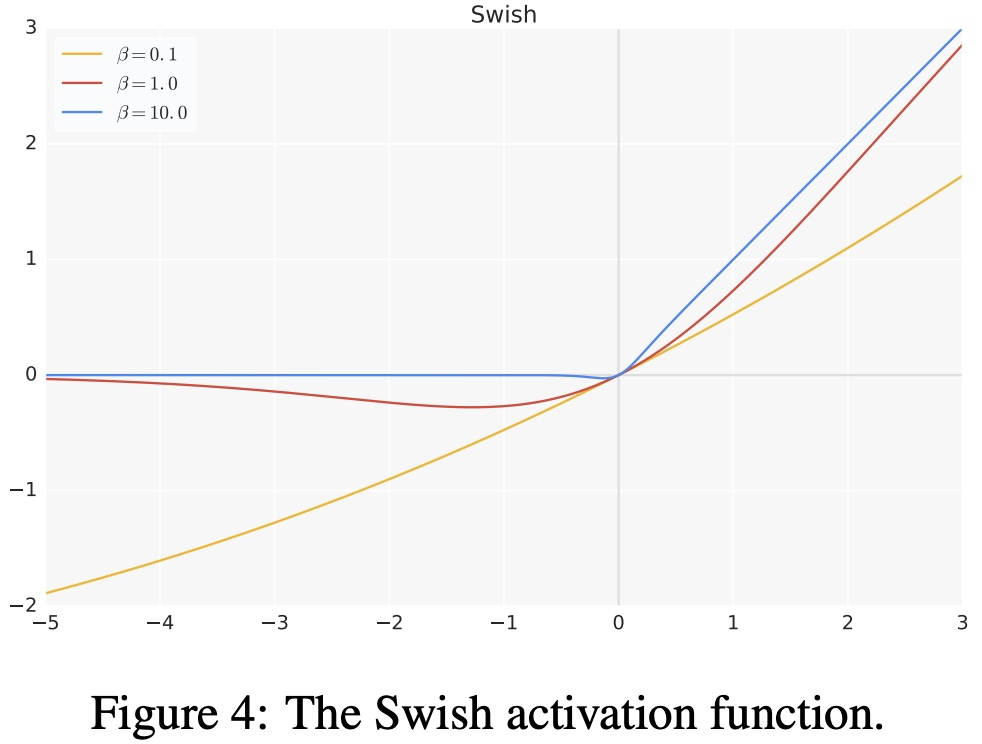
-
优点:
-
当 x>0时,不存在梯度消失的情况;当 x<0时,神经元也不会像 ReLU 一样出现死亡的情况;
-
swish处处可导,连续光滑;
-
swish并非一个单调的函数;
-
提升了模型的性能;
-
-
缺点:
- 计算量大;
3.3 hswish
函数定义:
f ( x ) = x R e L U 6 ( x + 3 ) 6 f\left(x\right)=x\frac{\mathrm{Re}L U6\left(x+3\right)}{6}\quad f(x)=x6ReLU6(x+3)

-
优点: 与 swish相比 hard swish减少了计算量,具有和 swish同样的性质。
-
缺点: 与 relu6相比 hard swish的计算量仍然较大。
4.激活函数的选择
-
浅层网络在分类器时,sigmoid函数及其组合通常效果更好。
-
由于梯度消失问题,有时要避免使用 sigmoid和 tanh函数。
-
relu函数是一个通用的激活函数,目前在大多数情况下使用。
-
如果神经网络中出现死神经元,那么 prelu函数就是最好的选择。
-
relu函数只能在隐藏层中使用。
-
通常,可以从 relu函数开始,如果 relu函数没有提供最优结果,再尝试其他激活函数。
5. 激活函数相关问题总结
5.1 为什么 relu不是全程可微/可导也能用于基于梯度的学习?
从数学的角度看 relu在 0点不可导,因为它的左导数和右导数不相等;但在实现时通常会返回左导数或右导数的其中一个,而不是报告一个导数不存在的错误,从而避免了这个问题。
5.2 为什么 tanh的收敛速度比 sigmoid快?
tanh ′ ( x ) = 1 − tanh ( x ) 2 ∈ ( 0 , 1 ) s ′ ( x ) = s ( x ) ( 1 − s ( x ) ) ∈ ( 0 , 1 4 ] \begin{array}{c}\tanh^{'}\left(x\right)=1-\tanh\left(x\right)^{2}\in\left(0,1\right)\\ \\ s^{'}\left(x\right)=s\left(x\right)\left(1-s\left(x\right)\right)\in\left(0,\dfrac{1}{4}\right]\end{array} tanh′(x)=1−tanh(x)2∈(0,1)s′(x)=s(x)(1−s(x))∈(0,41]
由上面两个公式可知 tanh引起的梯度消失问题没有 sigmoid严重,所以 tanh收敛速度比 sigmoid快。
5.3 sigmoid 和 softmax 有什么区别?
-
二分类问题时 sigmoid和 softmax是一样的,都是求 cross entropy loss,而 softmax可以用于多分类问题。
-
softmax是 sigmoid的扩展,因为,当类别数 k=2时,softmax回归退化为 logistic回归。
-
softmax建模使用的分布是多项式分布,而 logistic则基于伯努利分布。
-
多个 logistic回归通过叠加也同样可以实现多分类的效果,但是 softmax回归进行的多分类,类与类之间是互斥的,即一个输入只能被归为一类;多 logistic回归进行多分类,输出的类别并不是互斥的,即”苹果”这个词语既属于”水果”类也属于”3C”类别。
的梯度消失问题没有 sigmoid严重,所以 tanh收敛速度比 sigmoid快。
5.3 sigmoid 和 softmax 有什么区别?
-
二分类问题时 sigmoid和 softmax是一样的,都是求 cross entropy loss,而 softmax可以用于多分类问题。
-
softmax是 sigmoid的扩展,因为,当类别数 k=2时,softmax回归退化为 logistic回归。
-
softmax建模使用的分布是多项式分布,而 logistic则基于伯努利分布。
-
多个 logistic回归通过叠加也同样可以实现多分类的效果,但是 softmax回归进行的多分类,类与类之间是互斥的,即一个输入只能被归为一类;多 logistic回归进行多分类,输出的类别并不是互斥的,即”苹果”这个词语既属于”水果”类也属于”3C”类别。