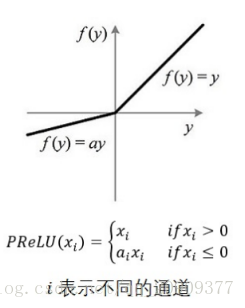
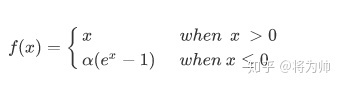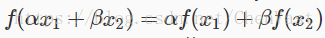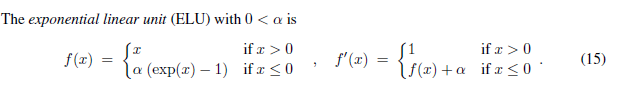【Python–torch】激活函数(sigmoid/softmax/ELU/ReLU/LeakyReLU/Tanh)

1. 介绍

激活函数（activation function）的作用是去线性化，神经网络节点的计算就是加权求和，再加上偏置项：

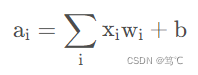
这是一个线性模型，将这个计算结果传到下一个节点还是同样的线性模型。只通过线性变换，所有的隐含层的节点就无存在的意义。原因如下：假设每一层的权值矩阵用 $W^{(i)}$ 表示，那么存在一个 $W^{\prime }$ 使得：

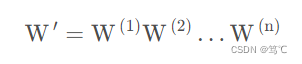
那么，n层隐含层就可以全部变成一个隐含层，隐含层的数量就没有任何意义。所以使用激活函数将其去线性化。这样可以使$W^{\prime }=W^{(1)}{W}^{(2)}...W^{(n)}$ 不再成立，每层隐含层都有其存在的意义。

2. 常用激活函数说明

2.1 Sigmoid

2.1.1 公式

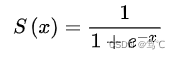
该函数输入为任意形状，输出形状与输入形状保持一致，此操作是将所有元素映射到(0,1)范围内，推导如下：

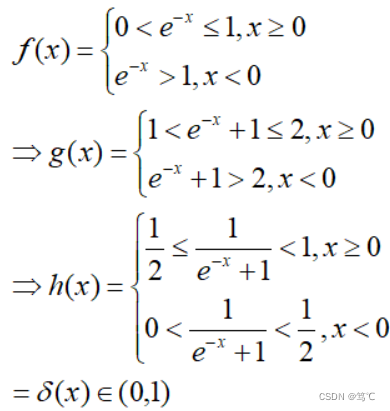
2.1.2 图像

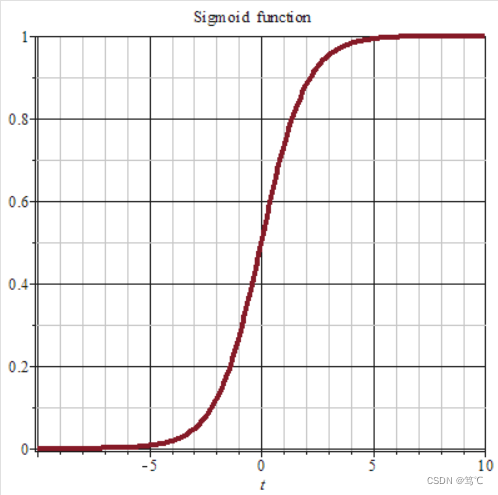
2.1.3 代码解读

三种用法：

1. torch.tanh(Tensor)
2. F.tanh(Tensor)
3. tanh = torch.nn.Tanh(); tanh(Tensor) # 先定义类，再调用

>>> import torch
>>> import torch.nn.functional as F>>> inp=torch.tensor(10,dtype=torch.float32) # 标量、向量（一维）、多维tensor均可# 第一种用法
>>> torch.sigmoid(inp)
tensor(1.0000)# 第二种用法，目前已经被丢弃
>>> F.sigmoid(inp)
UserWarning: nn.functional.sigmoid is deprecated. Use torch.sigmoid instead. warnings.warn("nn.functional.sigmoid is deprecated. Use torch.sigmoid instead.")
tensor(1.0000)# 第三种用法
>>> torch.nn.Sigmoid(inp)	# 报错
TypeError: __init__() takes 1 positional argument but 2 were given
# 这种情况下，需要先对类实例化，也就是这样：
>>> sigmoid = torch.nn.Sigmoid()
>>> sigmoid(inp)
tensor(1.0000)

2.2 Softmax

2.2.1 公式

• 中文名：归一化指数函数；
• 外文名：Normalized exponential function；
• 别 名：Softmax函数
• 领 域：人工智能
• 定 义：使每一个元素的范围在(0,1)之间
• 应 用：多分类问题
  

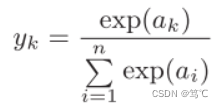
2.2.2 代码解读

>>> import torch
>>> import torch.nn.functional as F>>> inp=torch.tensor([10,20,5,3],dtype=torch.float32) # 向量（一维）、多维tensor均可# 第一种用法
>>> torch.softmax(inp, dim = 0) # 须指明dim（维度）
tensor([4.5398e-05, 9.9995e-01, 3.0589e-07, 4.1397e-08])# 第二种用法
>>> F.sigmoid(inp, dim = 0)
tensor([4.5398e-05, 9.9995e-01, 3.0589e-07, 4.1397e-08])# 第三种用法，跟sigmoid类似
>>> softmax = torch.nn.Softmax(dim = 0) # 默认维度dim为0，也可以传其他维度
>>> softmax(inp)
tensor([4.5398e-05, 9.9995e-01, 3.0589e-07, 4.1397e-08])

softmax0 = torch.nn.Softmax(dim=0)
softmax1 = torch.nn.Softmax(dim=1)
inp = torch.tensor([[1., 4., 8.],[8., 0., 5.]])
print("inp:",inp)
out0 = softmax0(inp)
print("out:",out0)
total_sum0 = torch.sum(out0)
print("sum:",total_sum0)# print-------------------
inp: tensor([[1., 4., 8.],[8., 0., 5.]])
out: tensor([[9.1105e-04, 9.8201e-01, 9.5257e-01],[9.9909e-01, 1.7986e-02, 4.7426e-02]])
sum: tensor(3.)print("inp:",inp)
out1 = softmax1(inp)
print("out:",out1)
total_sum1 = torch.sum(out1)
print("sum:",total_sum1)# print------------------
inp: tensor([[1., 4., 8.],[8., 0., 5.]])
out: tensor([[8.9468e-04, 1.7970e-02, 9.8114e-01],[9.5227e-01, 3.1945e-04, 4.7411e-02]])
sum: tensor(2.)

2.3 ELU

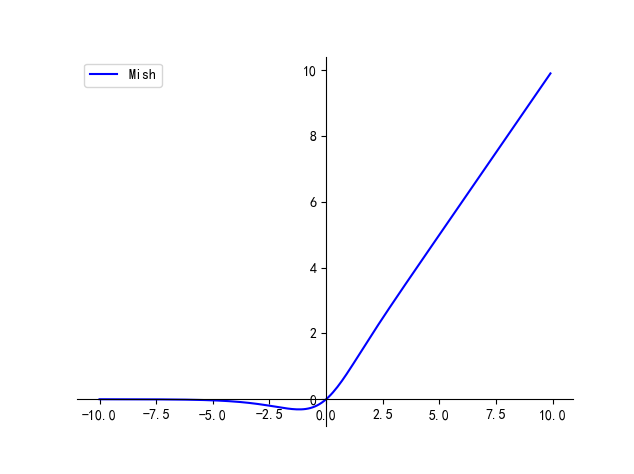
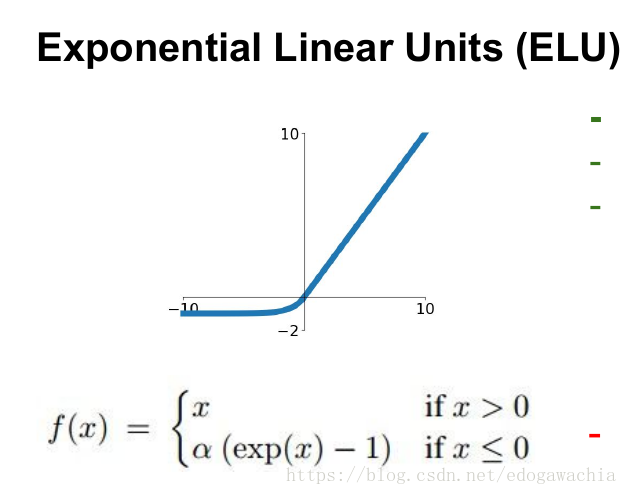
• 指数线性单元函数：该函数是在元素级别进行操作，既将输入中所有特征元素进行公式中所示操作。
• 该函数输入为任意形状，输出形状与输入保持一致。

2.3.1 公式

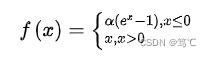
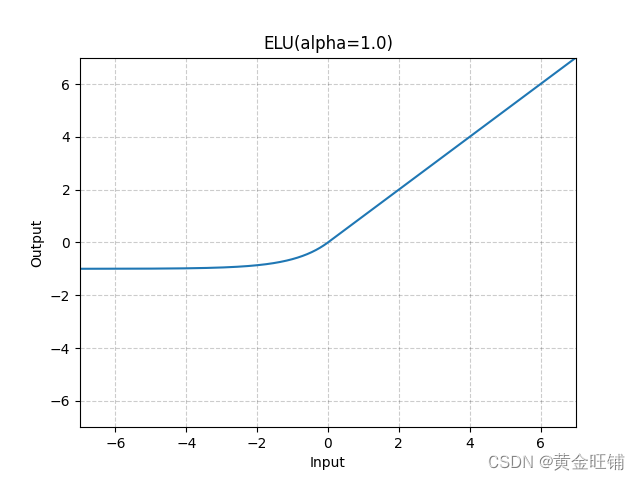
2.3.2 图像

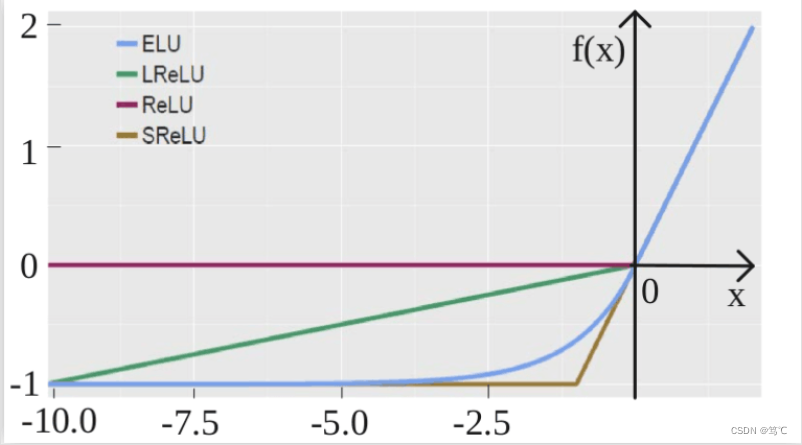
2.3.3 代码解读

1. F.elu(Tensor, alpha=1.0, inplace=False)	# 直接调用2. torch.nn.ELU(	# 先定义类，再调用alpha=1.0,  # alpha默认为1inplace=False)  # 该参数可选，默认为False，若为True则表示输入变量在内存中存储的值被计算结果覆盖

1）使用方法

import torch.nn.functional as F
import torch# 第一种用法
elu = torch.nn.ELU() # 先定义类
elu(Tensor) # 再调用# 第二种用法
F.elu(Tensor, alpha=1.0, inplace=False)# 1.标量
inp=torch.tensor(-2.5,dtype=torch.float32)
# tensor(-0.9179, device='cuda:0')# 2.向量/列表
inp=torch.tensor([10,-2.5])
# tensor([10.0000, -0.9179])# 3.二维数组
inp=torch.tensor([[1,-2.5],[0,10]])
# tensor([[ 1.0000, -0.9179],
#         [ 0.0000, 10.0000]])

2）inplace参数验证

import torch
import torch.nn as nninp=torch.tensor(-2.5,dtype=torch.float32).to(device)elu=nn.ELU(inplace=False)print("inp address:",id(inp))  # 查看变量在内存中的位置
out=elu(inp)
print("out address:",id(out))
print(out)  # tensor(-0.9179, device='cuda:0')
print(inp)  # 验证elu运算之后inp变量值是否被覆盖# print------------
# inp address: 1892728046504
# out address: 1892728156304
# tensor(-0.9179, device='cuda:0')
# tensor(-2.5000, device='cuda:0')elu=nn.ELU(inplace=True)
inp=torch.tensor(-2.5,dtype=torch.float32).to(device)print("inp address:",id(inp))  # 查看变量在内存中的位置
out=elu(inp)
print("out address:",id(out))
print(out)  # tensor(-0.9179, device='cuda:0')
print(inp)  # 验证elu运算之后inp变量值是否被覆盖# print----------
# inp address: 1924575957856
# out address: 1924575957856
# tensor(-0.9179, device='cuda:0')
# tensor(-0.9179, device='cuda:0')

2.4 ReLU

• 整流线性单元函数。该激活函数最为常用，以y轴划分，左面恒为0，右面为y=x。
• 其输入为任意形状，输出与输入形状保持一致；操作在元素级别进行；
  inplace参数表示是否采用计算结果替换原始输入；

2.4.1 公式

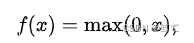
2.4.2 图像

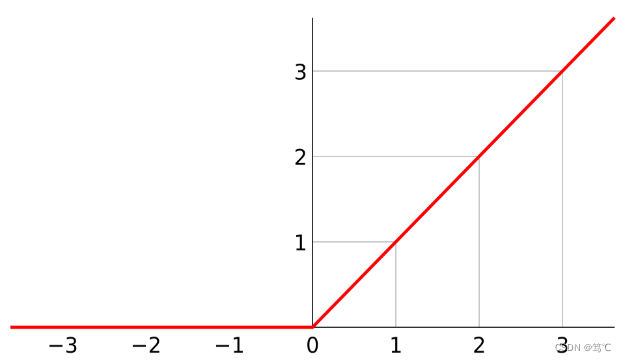
2.4.3 代码解读

两种用法同ELU，这里只介绍其中一种。

import torch.nn.functional as F
import torch# 两种用法同ELU，这里只介绍其中一种
relu=torch.nn.ReLU()# 1.标量
# inp=torch.tensor(2.5)
# out: tensor(2.5000)# 2.向量
# inp=torch.tensor([2.5,0,-10,25])
# out: tensor([ 2.5000,  0.0000,  0.0000, 25.0000])# 3.二维数组
inp=torch.tensor([[2.5,0],[-10,25]])
# out: tensor([[ 2.5000,  0.0000],
#         [ 0.0000, 25.0000]])out=relu(inp)
print("out:",out)

2.5 ReLU6

• ReLU6 就是普通的 ReLU 但是限制最大输出为 6，这是为了在移动端设备 float16/int8 的低精度的时候也能 有很好的数值分辨率。如果对 ReLU 的激活范围不加限制，输出范围为 0 到正无穷，如果激 活值非常大，分布在一个很大的范围内，则低精度的 float16/int8 无法很好地精确描述如此大范围的数值，带来精度损失。在 MobileNet 中使用 ReLU6。
• 解释：y轴划分，左面恒为0；右面当x<=6时为y=x，此外一直保持y=6。此函数对ReLU函数的上限做了一定的限制，缩小了参数搜索范围。
• 其输入为任意形状，输出与输入形状保持一致；操作在元素级别进行；inplace参数表示是否采用计算结果替换原始输入；

2.5.1 公式

$f(x)=min(max(0,x),6)$

2.5.2 图像

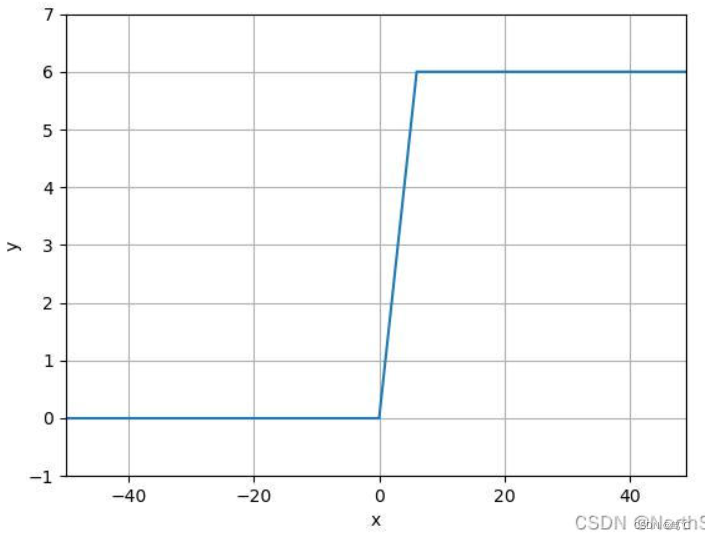
2.5.3 代码解读

用法，同ELU和ReLU。

import torch
relu=torch.nn.ReLU6()
# 1.标量
inp=torch.tensor(2.5)
# out: tensor(2.5000)# 2.向量
# inp=torch.tensor([2.5,0,-10,25])
# out: tensor([ 2.5000,  0.0000,  0.0000, 6.0000])# 3.二维数组
inp=torch.tensor([[2.5,0],[-10,25]])
# out: tensor([[ 2.5000,  0.0000],
#         [ 0.0000, 6.0000]])out=relu(inp)
print("out:",out)

2.6 LeakyReLU

• LeakyReLU函数是一种新的神经网络单元激活函数，它的出现改变了深度神经网络的运行方式。Leaky ReLU函数是一个非线性函数，用于增加模型的表现力，并使网络nerual更好地拟合数据。
• 因为Leaky ReLU函数允许负数值通过，这使得动态范围变得更宽，这将有助于解决许多深度学习问题，如梯度消失的问题。梯度消失是一种情况，当神经网络的某些层变得比其他层更深，梯度开始变得很小，而神经元几乎不更新，这会影响模型的性能。使用Leaky ReLU函数可以解决梯度消失的问题，因为它能够保证层之间的更新效果。
• Leaky ReLU函数是标准ReLU函数的一个变体，它包含一个新的参数n，允许负数值通过一个小的数量，而不是被设置为零。因此，Leaky ReLU函数可以让神经元更容易激活，对比标准ReLU函数。
• Leaky ReLU函数还可以防止神经元抖动。当神经元的输出是大于零的负数时，梯度下降算法会有很大的峰值，这会使梯度下降变得缓慢或不稳定，从而影响训练速度。使用Leaky ReLU函数，小的负数值的梯度不会被置为零，抑制抖动。
• 另一个Leaky ReLU函数的优点是它可以更好地拟合模型，这得益于低值的gradient。梯度下降算法在计算梯度时，Leaky ReLU函数可以使用低值的梯度，这将使模型得到更快的收敛，从而提高模型的性能。
• 虽然Leaky ReLU函数有许多优点，但它也有一些缺点。由于LeakyReLU函数具有负值，它可能会导致潜在的问题，如激活数量可能会进一步减少，这会影响模型的性能。此外，Leaky ReLU 函数可能会使网络变得过拟合，从而导致网络性能下降。

总之，Leaky ReLU函数是一种新的神经网络单元激活函数，它可以改善深度神经网络的性能，利用它改善梯度消失和抖动的问题，并可以更好地拟合模型。虽然Leaky ReLU函数有许多优点，但它也有一些缺点，在使用Leaky ReLU函数时，应该注意避免出现这些缺点。

2.6.1 公式

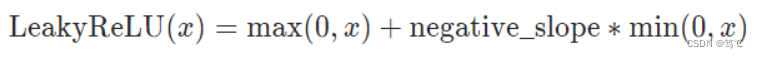
或

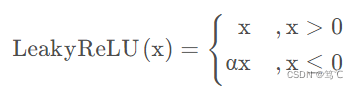
2.6.2 图像

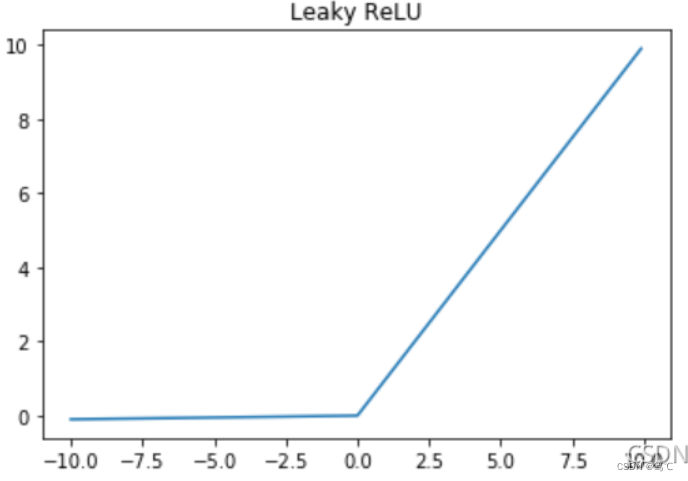
2.6.3 代码解读

注意此时，调用的第一种方法应该是：F.leaky_relu()，注意下划线。其余的使用方法和上面三种 LU 函数没有区别。

这里只介绍第二种方法：也就是先定义类，后调用。

torch.nn.LeakyReLU(negative_slope=0.01, inplace=False)

import torch
relu=torch.nn.LeakyReLU()
# 1.标量
# inp=torch.tensor(2.5)
# out: tensor(2.5000)# 2.向量
# inp=torch.tensor([2.5,0,-100,25])
# out: tensor([ 2.5000,  0.0000,  -1.0000, 25.0000])# 3.二维数组
inp=torch.tensor([[2.5,0],[-100,25]])
# out: tensor([[ 2.5000,  0.0000],
#         [ -1.0000, 25.0000]])out=relu(inp)
print("out:",out)

2.7 Tanh

• 双曲正切函数：该函数现常用于神经网络最后一层。
• 该函数输入为任意形状，输出与输入形状保持一致；操作在元素级别进行；

2.7.1 公式

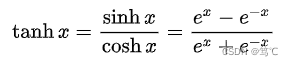
此操作是将所有元素映射到(-1,1)范围内，推导如下：

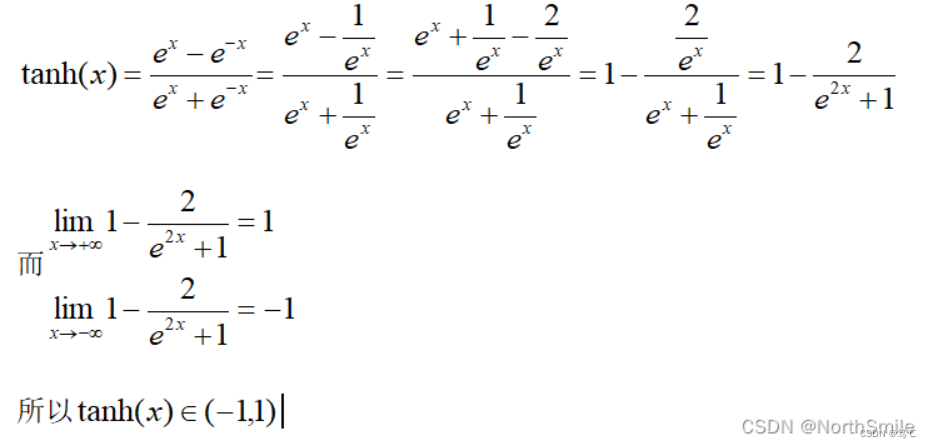
2.7.2 图像

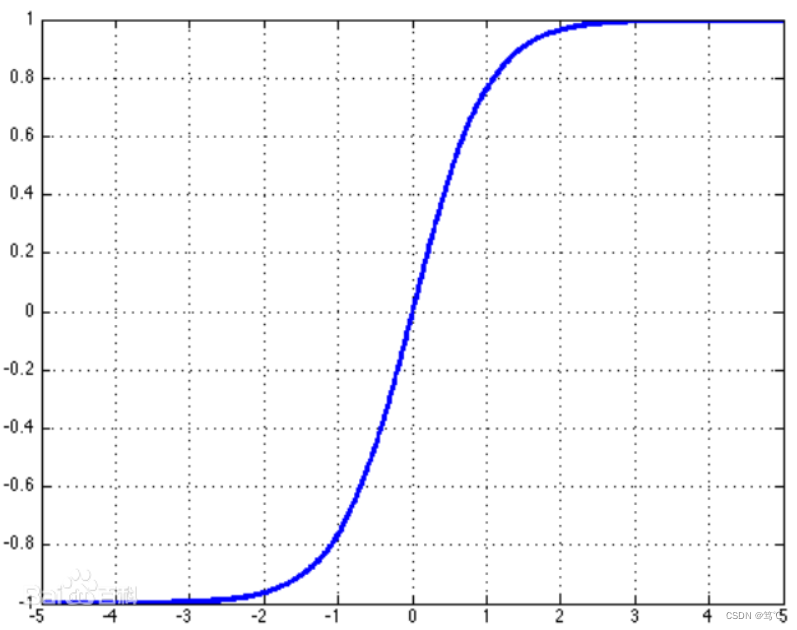
2.7.3 代码解读

该函数使用方法和sigmoid类似，也有三种使用方法：

1. torch.tanh(Tensor)
2. F.tanh(Tensor)
3. tanh = torch.nn.Tanh(); tanh(Tensor)

下面只介绍第三种：

tanh=nn.Tanh()
# 1.标量
inp=torch.tensor(2.5)
# out: tensor(0.9866)# 2.向量
# inp=torch.tensor([2.5,0,-10,25])
# out: tensor([ 0.9866,  0.0000, -1.0000,  1.0000])# 3.二维数组
# inp=torch.tensor([[2.5,0],
#                   [-10,25]])
# out: tensor([[ 0.9866,  0.0000],
#         [-1.0000,  1.0000]])out=tanh(inp)
print("out:",out)

3. 总结

That’s all. 欢迎指正。