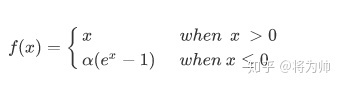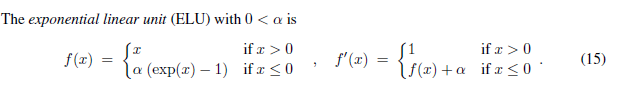---

楼主最近在研究激活函数，索性将常用的激活函数进行了简单的整理，方便以后翻看，也希望能帮到你。

---

1、sigmoid函数

函数表达式：f(x) = 1/(1+e^-x)
函数特点：
优点：1.输出[0,1]之间；2.连续函数，方便求导。
缺点：1.容易产生梯度消失；2.输出不是以零为中心；3.大量运算时相当耗时（由于是幂函数）。函数定义：
def sigmoid(x):y = 1/(1+np.exp(-x))return y

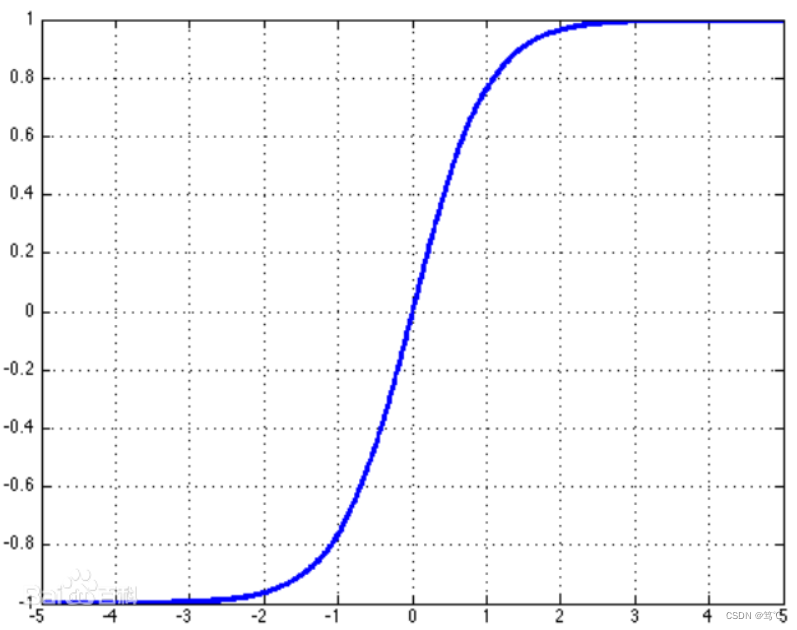
2、tanh函数

函数表达式：f(x) = (e^x-e^-x)/(e^x+e-x)
函数特点：
优点：1.输出[-1,1]之间；2.连续函数，方便求导；3.输出以零为中心。
缺点：1.容易产生梯度消失； 2.大量数据运算时相当耗时（由于是幂函数）。函数定义：
def tanh(x):y = (np.exp(x) - np.exp(-x))/(np.exp(x) + np.exp(-x))return y

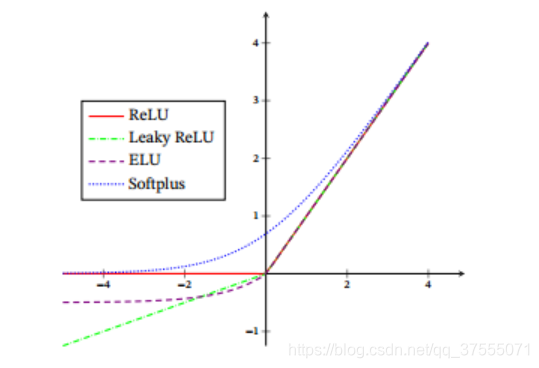
3、ReLu函数

函数表达式： f(x)=  当x<0  f(x)=0； 当x>=0 f(x)=x
函数特点：
优点：1.解决了正区间梯度消失问题；2.易于计算； 3.收敛速度快
缺点：1.输出不是以零为中心；2.某些神经元不能被激活，导致参数永远不能更新。函数定义：
def ReLU(x):y = []for i in x:if i >= 0:y.append(i)else:y.append(0)return y

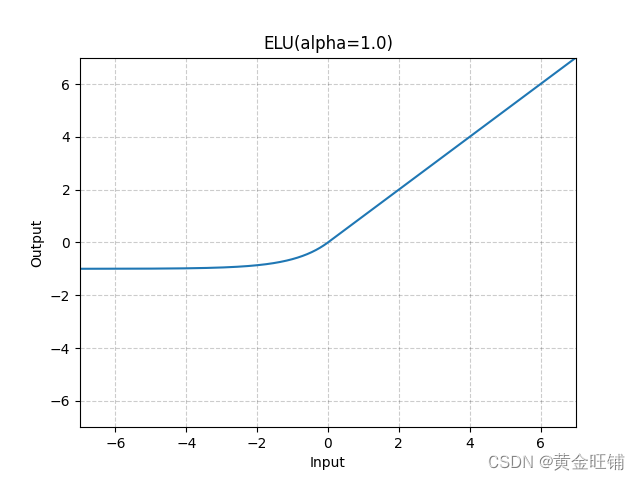
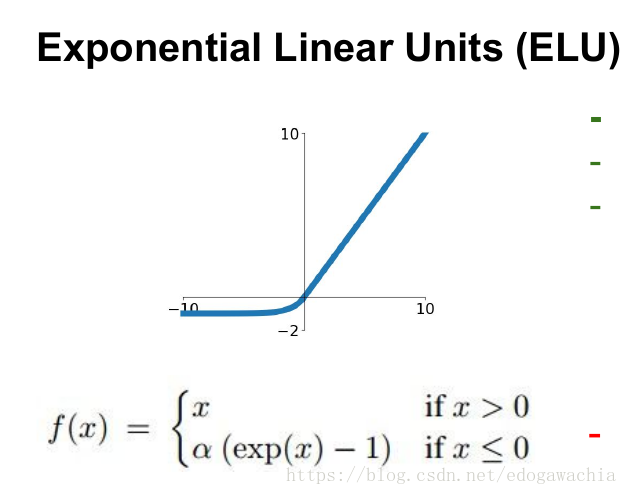
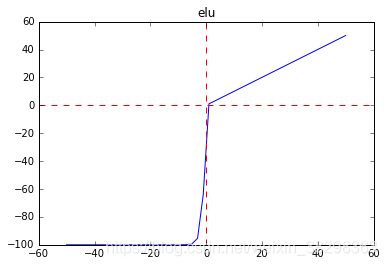
4、elu函数

函数表达式： f(x)=  当x>=0  f(x)=x；  当x<0  f(x) =a(e^x -1)
函数特点：
优点：1.解决了正区间梯度消失问题；2.易于计算；3.收敛速度快；4.解决了某些神经元不能被激活问题；5.输出的均值为0
缺点：输出不是以零为中心函数定义：
def elu(x, a):y = []for i in x:if i >= 0:y.append(i)else:y.append(a*(np.exp(i)-1))return y

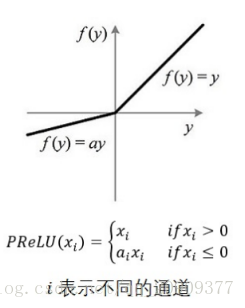
5、leaky ReLU函数

函数表达式： f(x)=  当x>=0  f(x)=x； 当x<0  f(x) =0.01x
函数特点：
优点：1.解决了正区间梯度消失问题；2.易于计算；3.收敛速度快；4.解决了某些神经元不能被激活
缺点：输出不是以零为中心函数定义：
def LReLU(x):y = []for i in x:if i >= 0:y.append(i)else:y.append(0.01*i)return y

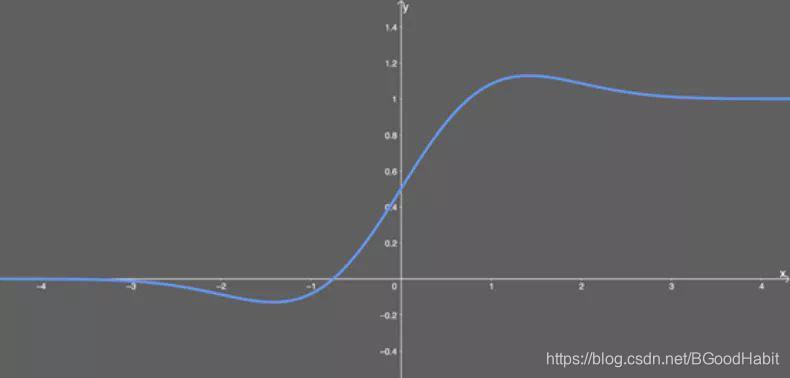
6、softplus函数

函数表达式： y = ln(1+e^x)
函数定义：
def softplus(x):y = np.log(1 + np.exp(x))return y

7、softmax函数

函数表达式：输入信号的指数函数除以所有输入信号的指数和
函数特点：一般用在分类的输出层作为激活函数
优点：1.输出在[0,1]之间，可以当初概率。
缺点： 在实际问题中，由于幂运算需要时间，而且softmax不会影响各元素的大小，因此输出层的softmax激活函数一般被省略。
函数定义：
def softmax(x):c = np.max(x)   # 解决溢出问题exe_x = np.exp(x)exe_s = np.sum(exe_x)y = exe_x/exe_sreturn y

绘制函数的代码

#!/usr/bin/env python
# -*- coding: utf-8 -*-
# Author：'ZhangML' 
# Time:2021/1/2  15:56from matplotlib import pyplot as plt
import numpy as np
import mathx = np.linspace(-6, 6, 200)
# 1.sigmoid函数的表达式：f(x) = 1/(1+e^-x)
# 函数特点：
# 优点：1.输出[0,1]之间；2.连续函数，方便求导。
# 缺点：1.容易产生梯度消失；2.输出不是以零为中心；3.大量运算时相当耗时（由于是幂函数）。def sigmoid(x):y = 1/(1+np.exp(-x))return y# 2.tanh的函数表达式： f(x) = (e^x-e^-x)/(e^x+e-x)
# 函数特点：
# 优点：1.输出[-1,1]之间；2.连续函数，方便求导；3.输出以零为中心。
# 缺点：1.容易产生梯度消失； 2.大量数据运算时相当耗时（由于是幂函数）。
def tanh(x):y = (np.exp(x) - np.exp(-x))/(np.exp(x) + np.exp(-x))return y# 3. ReLu 的函数表达式： f(x)=  当x<0  f(x)0   当x>=0 f(x) = x
# 函数特点：
# 优点：1.解决了正区间梯度消失问题；2.易于计算； 3.收敛速度快
# 缺点：1.输出不是以零为中心；2.某些神经元不能被激活，导致参数永远不能更新。
def ReLU(x):y = []for i in x:if i >= 0:y.append(i)else:y.append(0)return y# return np.maximum(x,[0]*100)   #可以利用np中的maximum方法表示，也可以用上述方法# 4.elu 的函数表达式  f(x)   x>=0  f(x)=x   x<0  f(x) =a(e^x -1)
# 函数特点：
# 优点：1.解决了正区间梯度消失问题；2.易于计算；3.收敛速度快；4.解决了某些神经元不能被激活问题；5.输出的均值为0
# 缺点：输出不是以零为中心
def elu(x, a):y = []for i in x:if i >= 0:y.append(i)else:y.append(a*(np.exp(i)-1))return y# 5.leaky ReLU 的函数表达式  x>=0  f(x)=x   x<0  f(x) =0.01x
# 函数特点：
# 优点：1.解决了正区间梯度消失问题；2.易于计算；3.收敛速度快；4.解决了某些神经元不能被激活
# 缺点：输出不是以零为中心
def LReLU(x):y = []for i in x:if i >= 0:y.append(i)else:y.append(0.01*i)return y# 6.softplus函数的表达式： y = ln(1+e^x)
def softplus(x):y = np.log(1 + np.exp(x))return y# softmax激活函数   softmax的表达式为：输入信号的指数函数除以所有输入信号的指数和
# 函数特点：一般用在分类的输出层作为激活函数
# 优点：1.输出在[0,1]之间，可以当初概率。
# 缺点： 在实际问题中，由于幂运算需要时间，而且softmax不会影响各元素的大小，因此输出层的softmax激活函数一般被省略。
def softmax(x):c = np.max(x)   # 解决溢出问题exe_x = np.exp(x)exe_s = np.sum(exe_x)y = exe_x/exe_sreturn yfont1 = {'family': 'Times New Roman', 'weight': 'normal', 'size': 15}# 绘制整张图
ax = plt.subplot(111)
plt.plot(x,sigmoid(x),c="lime",lw="2",label = "Sigmiod")      # 绘制sigmoid函数
plt.plot(x,tanh(x),c="deeppink",lw="2",label = "Tanh")        # 绘制tanh函数
plt.plot(x,softmax(x),c="green",lw="2",label = "Softmax")     # 绘制softmax函数
plt.plot(x,ReLU(x),c="blue",lw="2",label="ReLU")              # 绘制ReLU函数
plt.plot(x,elu(x,0.1),c="darkviolet",lw="2",label="elu")      # 绘制elu函数
plt.plot(x,LReLU(x),c="springgreen",lw="2",label="LReLU")     # 绘制LReLU函数
plt.plot(x,softplus(x),c="red",lw="2",label="Softplus")       # 绘制Softplus函数
plt.gca().spines["bottom"].set_position(("data",0))           # 将函数图像移动到x轴（0,0）
plt.gca().spines["left"].set_position(("data",0))             # 将函数图形移动到y轴（0,0）
plt.xticks(fontproperties='Times New Roman', fontsize=18, )
plt.yticks(fontproperties='Times New Roman', fontsize=18, )
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
plt.legend(loc="best", frameon=False, prop=font1)
plt.show()

运行效果如下图所示：

这里有直接使用keras库中的激活函数绘图的，大同小异，想了解的可以看看，送上传送门，希望可以帮到你。