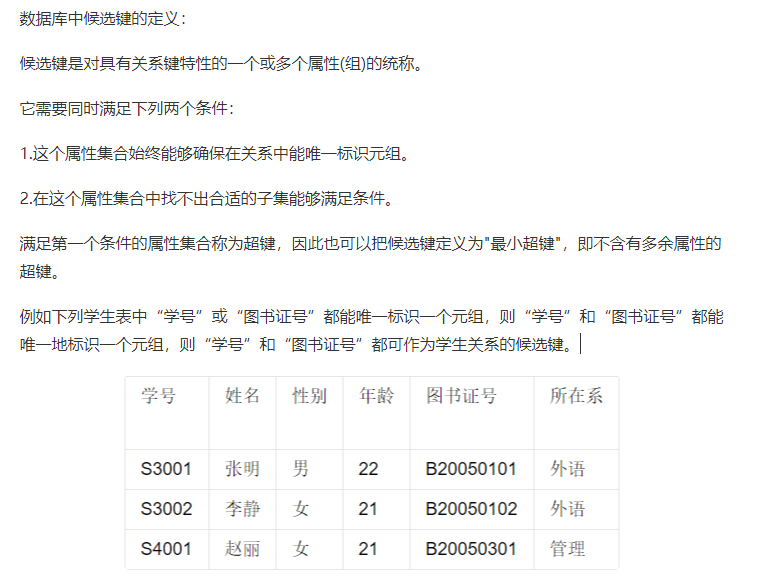
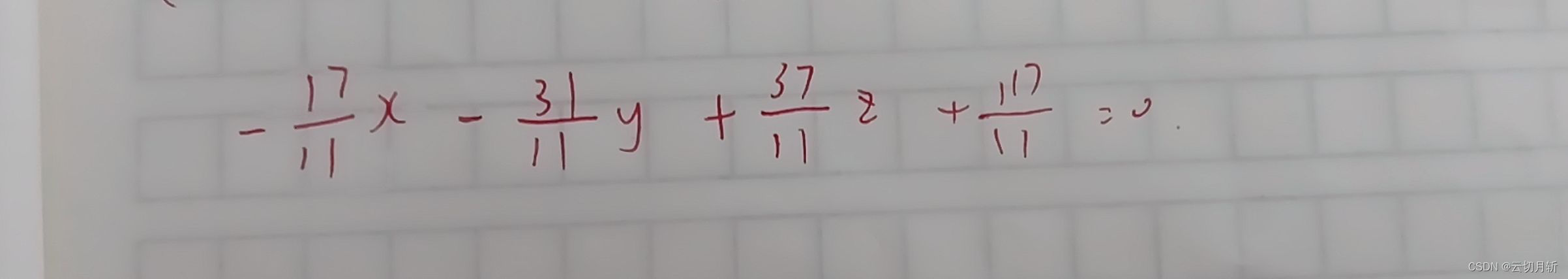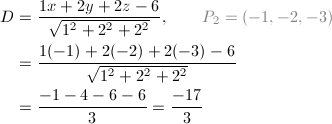什么是关键码？

设关系模式R的属性集是U，X是U的一个子集，F是在R上成立的一个函数依赖集。如果X→U在R上成立（即X→U在中），那么称X是R的一个超键。如果X→U在R上成立，但对X的任一真子集都有→U不成立（即→U不在中，或者XU)，那么称X是R上的一个候选键。
 

快速求解候选键的一个充分条件

对于给定的关系模式RE(,  , … ,  )和函数依赖集F，可将其属性分为以下四类。

（1）L类：仅出现在F中的函数依赖左部的属性；
（2）R类：仅出现在F的函数依赖右部的属性；
（3）N类：在F的函数依赖左右两边均未出现的属性；
（4）LR类：在F的函数依赖左右两边均出现的属性。

对于给定的关系模式R及其函数依赖集F，有一下结论。

（1）若X（X∈RE）是L类属性，则X必为RE的任意候选键的成员；
（2）若X（X∈RE）是L类属性，且包含了RE的全部属性，则X必为RE的唯一候选键；
（3）若X（X∈RE）是R类属性，则X不在任何候选键中；
（4）若X（Y∈RE）是N类属性，则X包含在R的任一候选键中；
（5）若X（X∈RE）是RE的N类和L类属性组成的属性集，且X包含了R的全部属性，则X
是RE的唯一候选键。

 

下面我们举例说明。

【例1】设有关系模式R(A, B, C, D)与它的函数依赖集F={D→B, B→D, AD→B, AC→D}，求R的所有候选键。

解题思路：

通过考察F发现，A，C两属性是L类属性，故A、C两属性必在R的任何候选键中；

又由于=ABCD，即包含了R的全部属性，因此，AC是R的唯一候选键。

 

【例2】设有关系模式R(A, B, C, D, E, P)与它的函数依赖集F={A→D, E→D, D→B, BC→D, DC→A}，求R的所有候选键。

解题思路：

通过考察F发现，C，E两属性是L类属性，故C，E两属性必在R的任何候选键中；

由于P是N类属性，故P属性也必在R的任何候选键中；

又由于= ABCDEP，即包含R的全部属性，因此，CEP是R的唯一候选键。

 

多属性函数依赖集候选键的求解算法

下面我们总结一下求解一个关系R的候选键的一般步骤：
（1）根据函数依赖集F，将R的所有属性分为L类、R类、N类和LR类等四类，并令X代表L类和N类属性，Y代表LR类属性；

（2）求，若包含了R的全部属性，则X即为R的唯一候选键，转到步骤（5）；

（3）从Y中取一个属性A，求，若它包含了R的全部属性，则XA是R的一个候选键，再换另一个属性反复进行这一过程，直到试完Y中所有的属性；
（4）这次每轮从Y中取两个、三个、多个属性并到属性集X中，每轮仿照步骤（3）的动作，耐心地求出关系R的全部候选键；

（5）停止，输出结果。

 

【例3】设有关系模式R(A, B, C, D, E)与它的函数依赖集F={A→BC, CD→E, B→D, E→A}，求R的所有候选键。
解题思路：

通过分析F发现，其所有的属性A、B、C、D、E都是LR类属性，没有L类、R类、N类属性；

因此，先从这些属性中依次取出一个属性，分别求它们关于F的闭包：

=ABCDE，=BD，=C，=D， =ABCDE

由于和都包含了R的全部属性，因此，属性A、E分别都是R的一个候选键；

接下来，从关系模式R中取出两个属性，分别求它们关于F的闭包，但在取出两个属性时，只能从B，C，D三个属性中取出两个属性，因为属性A、E已经是R的候选键了，根据候选键的定义，它们就不可能再存在于其他的候选键中：

=ABCDE，=ABCDE，=BD

由于和都包含了R的全部属性，因此，属性集BC，CD也分别都是R的一个候选键；

至此，关系模式R中不可能再存在别的候选键了，因此，关系模式R的所有的候选键分别是A、E、BC和CD。

 

 

 

参考资料：[1]陈志泊，王春玲，许福，范春梅.数据库原理及应用教程（第3版）[M].北京:人民邮电出版社，2014：136-137.