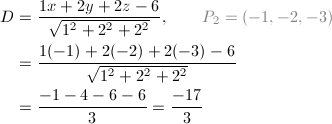---

前言

空间解析几何中有平面及其方程、空间直线及其方程、曲面及其方程、空间曲线及其方程，有时候就怀疑这个空间的真实性，高维空间中我们是怎样的存在，害，好像有点杞人忧天了，每天吃好、喝好、睡好、学习搞好就阿弥陀佛了，来进入正题吧。

---

一、平面及其方程

平面的点法式方程

已知平面上一点$M_0\left(x_0,y_0,z_0\right)$和平面的一个法向量$\vec{n}=\left(A,B,C\right)$
对于平面上任意一点
$$M\left(x,y,z\right)$$
三者满足
$$\vec{n}\cdot \overrightarrow{M_{0}M}=0$$
点法式方程为
$$A\left(x-x_0\right)+B\left(y-y_0\right)+C\left(z-z_0\right)=0$$

平面的一般方程

三元一次方程
$$Ax+By+Cz+D=0$$
其图形总是一个平面，称为平面的一般方程
该平面的法向量为
$$\vec{n}=\left(A,B,C\right)$$
通过原点的平面方程：$Ax+By+Cz=0$
平行于$x$轴的平面方程：$By+Cz+D=0$
平行于$y$轴的平面方程：$Ax+Cz+D=0$
平行于$z$轴的平面方程：$Ax+By+D=0$
平行于$xOy$平面的平面方程：$Cz+D=0$
平行于$yOz$平面的平面方程：$Ax+D=0$
平行于$xOz$平面的平面方程：$By+D=0$

平面的截距式方程

一平面与$x$轴、$y$轴、$z$轴的交点依次为$\left(a,0,0\right)\text{、}Q\left(0,b,0\right)\text{、}R\left(0,0,c\right)$
且$a\ne 0\text{、}b\ne 0\text{、}c\ne 0$
截距式方程为
$$\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1$$
$a$、$b$、$c$依次称为平面在$x$轴、$y$轴和$z$轴上的截距

两平面的夹角

平面${\Pi }_1$和平面${\Pi }_2$的法向量分别为$\overrightarrow{n_1}=\left(A_1,B_1,C_1\right)$和$\overrightarrow{n_2}=\left(A_2,B_2,C_2\right)$，两平面的夹角为$\theta$且$0\le \theta \le \frac{\pi }{2}$
平面${\Pi }_1$和平面${\Pi }_2$夹角的余弦为
$$\cos \theta =\frac{|A_1{A}_2+B_1{B}_2+C_1{C}_2|}{\sqrt{A_1^2+B_1^2+C_1^2}\sqrt{A_2^2+B_2^2+C_2^2}}$$

点到平面的距离公式

已知点$P_0\left(x_0,y_0,z_0\right)$和平面$Ax+By+Cz+D=0$
点到平面的距离
$$d=\frac{|A{x}_0+B{y}_0+C{z}_0+D|}{\sqrt{A^2+B^2+C^2}}$$

二、空间直线及其方程

空间直线的一般方程

两平面的交线即为一条空间直线
平面${\Pi }_1:A_{1}x+B_{1}y+C_{1}z+D_1=0$
平面${\Pi }_2:A_{2}x+B_{2}y+C_{2}z+D_2=0$
一般方程为
$$\{\begin{array}{l}{A}_{1}x+B_{1}y+C_{1}z+D_1=0\\ A_{2}x+B_{2}y+C_{2}z+D_2=0\end{array}$$

空间直线的对称式方程（点向式方程）

已知直线$L$上任意一点$M\left(x,y,z\right)$和点$M_0\left(x_0,y_0,z_0\right)$
直线$L$的方向向量为$\vec{s}=\left(m,n,p\right)$
则有$\overrightarrow{M{M}_0}=\lambda \vec{s}$
点向式方程为
$$\frac{x-x_0}{m}=\frac{y-y_0}{n}=\frac{z-z_0}{p}$$

空间直线的参数方程

令点向式方程等于$t$，即
$$\frac{x-x_0}{m}=\frac{y-y_0}{n}=\frac{z-z_0}{p}=t$$
则参数方程为
$$\{\begin{array}{l}x=x_0+mt\\ y=y_0+nt\\ z=z_0+pt\end{array}$$

两直线的夹角

直线$L_1$的方向向量为$\overrightarrow{s_1}=(m_1,n_1,p_1)$，直线$L_2$的方向向量为$\overrightarrow{s_2}=(m_2,n_2,p_2)$
两直线的夹角为$\phi$并且$0\le \phi \le \frac{\pi }{2}$
两直线夹角的余弦为
$$\cos \phi =\frac{|m_1{m}_2+n_1{n}_2+p_1{p}_2|}{\sqrt{m_1^2+n_1^2+p_1^2}\sqrt{m_2^2+n_2^2+p_2^2}}$$

直线与平面的夹角

其中直线与平面的夹角范围为$0\le \phi <\frac{\pi }{2}$
直线的方向向量为$\vec{s}=\left(m,n,p\right)$，平面的法向量为$\vec{n}=\left(A,B,C\right)$
直线与平面夹角的正弦为
$$\sin \phi =\frac{|Am+Bn+Cp|}{\sqrt{A^2+B^2+C^2}\sqrt{m^2+n^2+p^2}}$$

平面束方程

设直线$L$由方程组
$$\{\begin{array}{l}{A}_{1}x+B_{1}y+C_{1}z+D_1=0\\ A_{2}x+B_{2}y+C_{2}z+D_2=0\end{array}$$确定，其中$A_1\text{、}{B}_1\text{、}{C}_1\text{和}{A}_2\text{、}{B}_2\text{、}{C}_2$不成比例
通过直线$L$的所有平面的全体称为平面束
平面束方程为
$$A_{1}x+B_{1}y+C_{1}z+D_1+\lambda \left(A_{2}x+B_{2}y+C_{2}z+D_2\right)=0$$

三、曲面及其方程

旋转曲面

以一条平面曲线绕其平面上的一条直线旋转一周所成的曲面叫做旋转曲面，旋转曲线和定直线分别叫做旋转曲面的母线和轴。
譬如：曲线$C:f\left(y,z\right)=0$
其绕$z$轴旋转一周得到的的旋转曲面的方程为
$$f\left(\pm \sqrt{x^2+y^2},z\right)=0$$
即在空间直角坐标系中绕$z$轴旋转，曲线方程中$z$坐标不变，$y$坐标变为$\pm \sqrt{x^2+y^2}$即可得到旋转曲面的方程。

图中的黑色实线分别表示$x$轴、$y$轴和$z$轴

旋转单叶双曲面

将$xOz$坐标面上的双曲线
$$\frac{x^2}{a^2}-\frac{z^2}{c^2}=1$$
绕$z$轴旋转一周得到
旋转单叶双曲面方程为
$$\frac{x^2+y^2}{a^2}-\frac{z^2}{c^2}=1$$
图形
$三维视图$

$yOz视图$

$xOy视图$

旋转双叶双曲面

将$xOz$坐标面上的双曲线
$$\frac{x^2}{a^2}-\frac{z^2}{c^2}=1$$
绕$x$轴旋转一周得到
旋转双叶双曲面方程为
$$\frac{x^2}{a^2}-\frac{y^2+z^2}{c^2}=1$$
图形
$三维视图$

$yOz视图$

$xOy视图$

旋转椭球面

方程
$$\frac{x^2+y^2}{a^2}+\frac{z^2}{c^2}=1$$
图形
$三维视图$

$yOz视图$

$xOy视图$

柱面

直线$L$沿定曲线$C$平行移动形成的轨迹叫做柱面，定曲线$C$叫做柱面的准线，动直线$L$叫做柱面的母线
也可以这样认为：在三维坐标系中某个二维坐标面内的曲线沿另一条坐标轴堆叠起来的图形叫做柱面，所以柱面方程中一定只有两个未知量。
只有两个未知量的平面方程所表示的图形也是柱面，譬如：$x-z=0$

抛物柱面

譬如：$y=x^2$
图形
$三维视图$

$yOz视图$

$xOy视图$

椭圆柱面

譬如
$$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$$
图形
$三维视图$

$yOz视图$

$xOy视图$

双曲柱面

譬如
$$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$$
图形
$三维视图$

$yOz视图$

$xOy视图$

二次曲面

三元二次方程$F(x,y,z)=0$所表示的曲面称为二次曲面，把平面称为一次曲面
以下二次曲面均可以通过$xOy$、$yOz$或$xOz$面内的曲线绕某条坐标轴旋转然后伸缩变换得到，称为伸缩变形方法； 还可以通过截痕法来了解曲面形状（自行翻阅书本）

椭圆锥面

方程
$$\frac{x^2}{a^2}+\frac{y^2}{b^2}=z^2$$
图形
$三维视图$

$yOz视图$

$xOy视图$

椭球面

方程
$$\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1$$
图形
$三维视图$

$yOz视图$

$xOy视图$

单叶双曲面

方程
$$\frac{x^2}{a^2}+\frac{y^2}{b^2}-\frac{z^2}{c^2}=1$$
图形
$三维视图$

$yOz视图$

$xOy视图$

双叶双曲面

方程
$$\frac{x^2}{a^2}-\frac{y^2}{b^2}-\frac{z^2}{c^2}=1$$
图形
$三维视图$

$yOz视图$

$xOy视图$

椭圆抛物面

方程
$$\frac{x^2}{a^2}+\frac{y^2}{b^2}=z$$
图形
$三维视图$

$yOz视图$

$xOy视图$

双曲抛物面

方程
$$\frac{x^2}{a^2}-\frac{y^2}{b^2}=z$$
图形
$三维视图$

$yOz视图$

$xOy视图$

四、空间曲线及其方程

空间曲线的一般方程

空间曲线可以看作两个曲面的交线
设$F(x,y,z)=0$和$G(x,y,z)=0$是两个曲面的方程
空间曲线的一般方程为
$$\{\begin{array}{l}F\left(x,y,z\right)=0\\ G\left(x,y,z\right)=0\end{array}$$

空间曲线的参数方程

将空间曲线$C$上动点坐标$x$、$y$和$z$表示为参数$t$的函数得到空间曲线的参数方程
$$\{\begin{array}{l}x=x\left(t\right)\\ y=y\left(t\right)\\ z=z\left(t\right)\end{array}$$
譬如：$\{\begin{array}{l}{x}^2+y^2+z^2=9\\ y=x\end{array}$的参数方程为$\{\begin{array}{l}x=\frac{3}{\sqrt{2}}\cos \theta \\ y=\frac{3}{\sqrt{2}}\cos \theta \\ z=3\sin \theta \end{array}\left(0\le \theta \le 2\pi \right)$

空间曲线在坐标面上的投影

以$xOy$坐标面为例
将空间曲线$C$的一般方程消去变量$z$后得到方程$H(x,y)=0$，该方程表示的是曲线$C$关于$xOy$面的投影柱面，而该投影柱面与$xOy$面的交线叫做空间曲线$C$在$xOy$面上的投影曲线，简称投影。
投影的方程为
$$\{\begin{array}{l}H\left(x,y\right)=0\\ z=0\end{array}$$
其他坐标面与该坐标面的做法相同

---

总结

以上三维图形的绘制均是借助$matlab$软件实现的，相关代码请参考博客：空间中常见曲面图形的绘制(matlab)
文章中绘制的三维图形在这里可以找到
链接：https://pan.baidu.com/s/1-VgPeuLABTe91_LPlCG4eg
提取码：zjmd