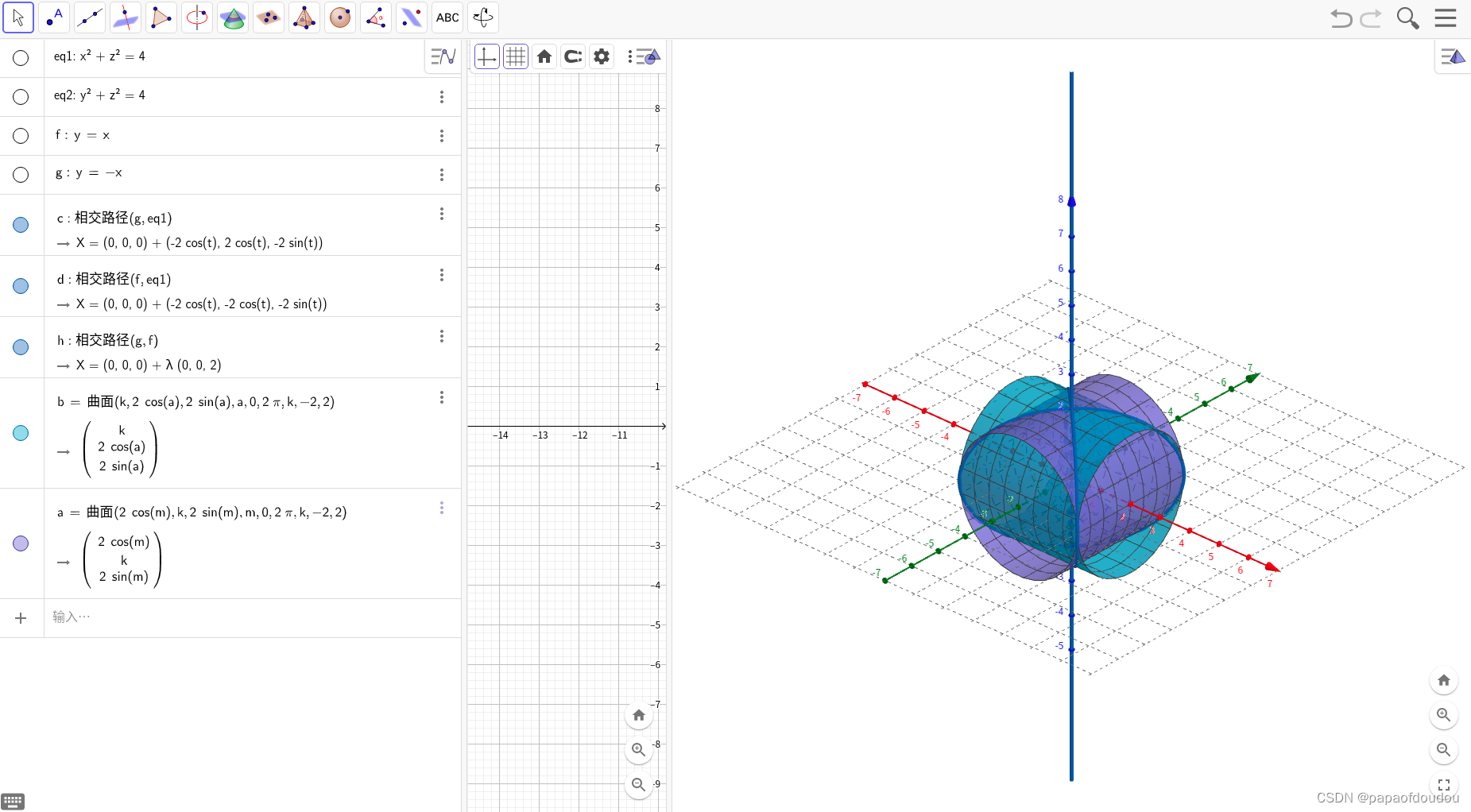
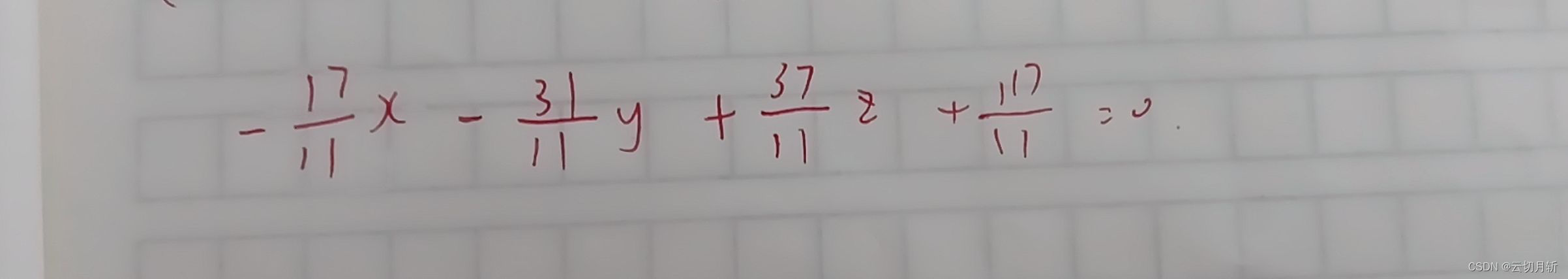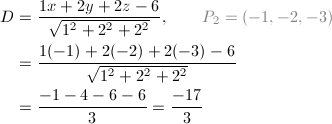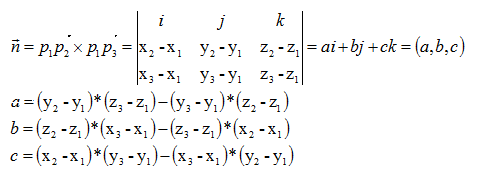空间曲面构造及其方程

article/2025/8/30 12:15:31

１.旋转单叶双曲面

　旋转单叶双曲面是直纹面，它的构造有多种方式，先看其中一种:

　设直线的参数方程为：

　 $\left\{\begin{matrix} x=1\\ y=t \ \\ z=2t \end{matrix}\right.\quad t> -5 \wedge t<5$

则通过geogebra命令

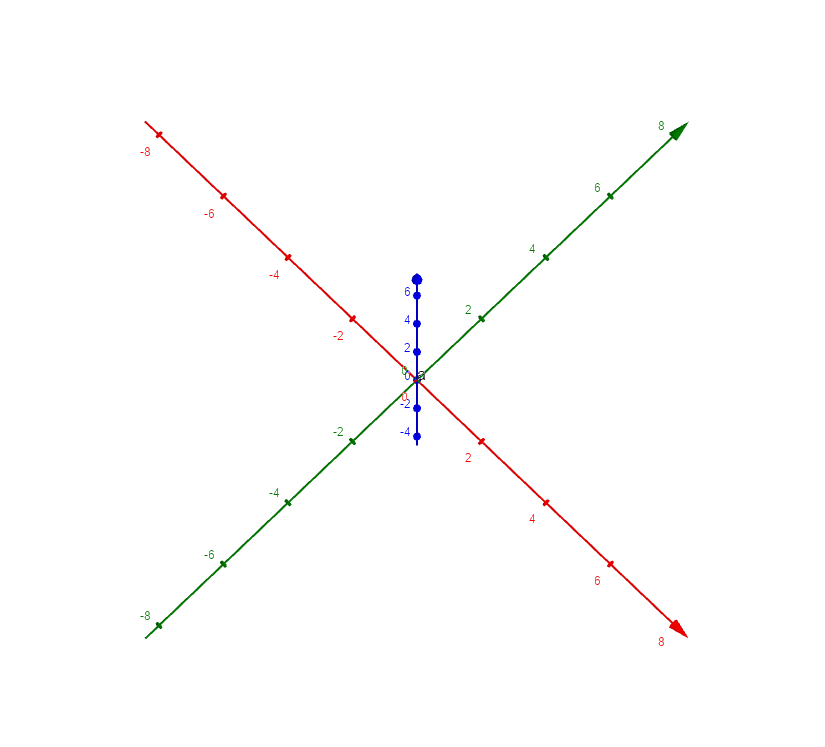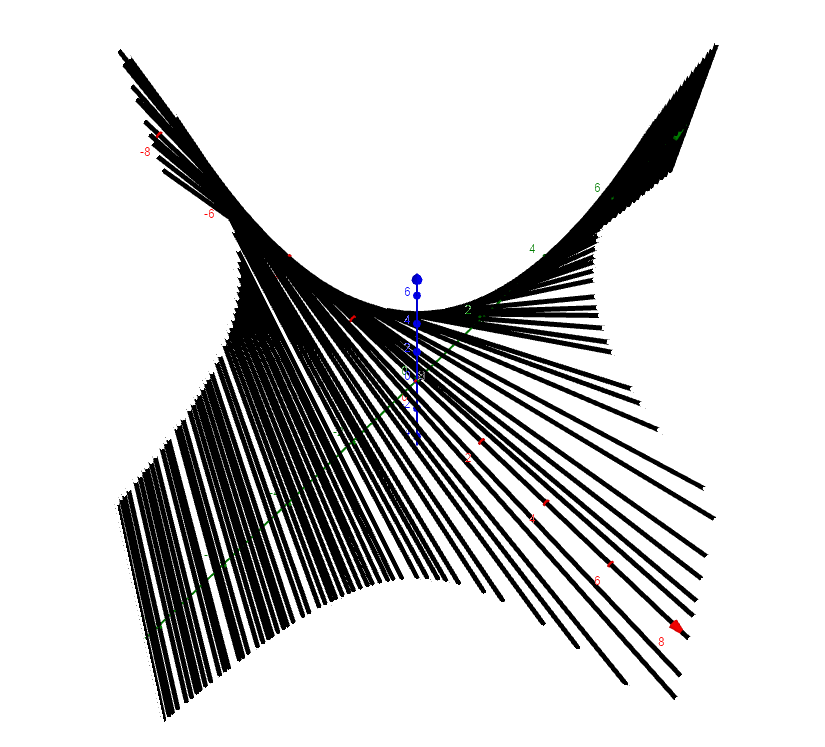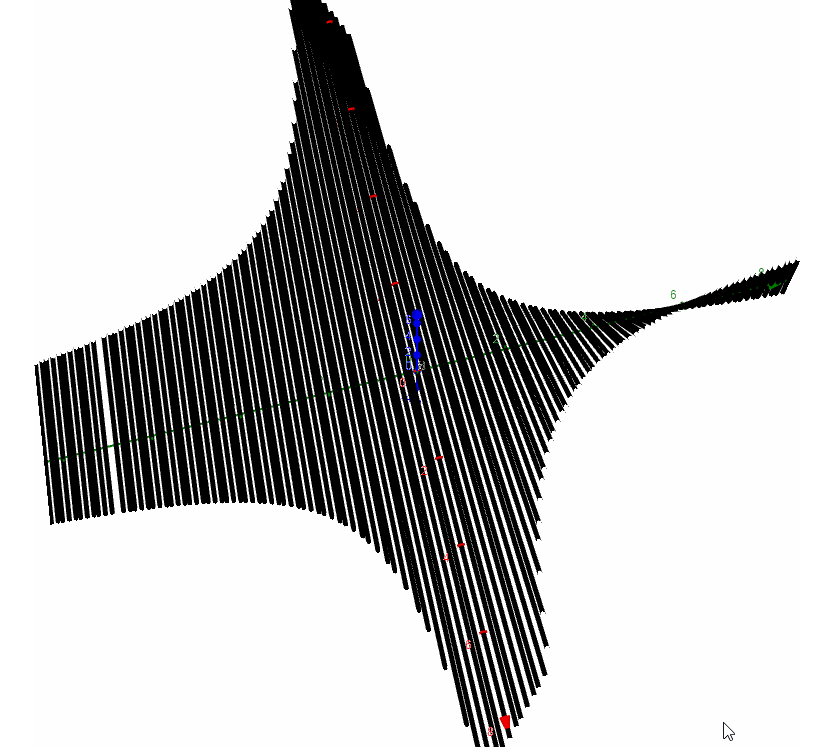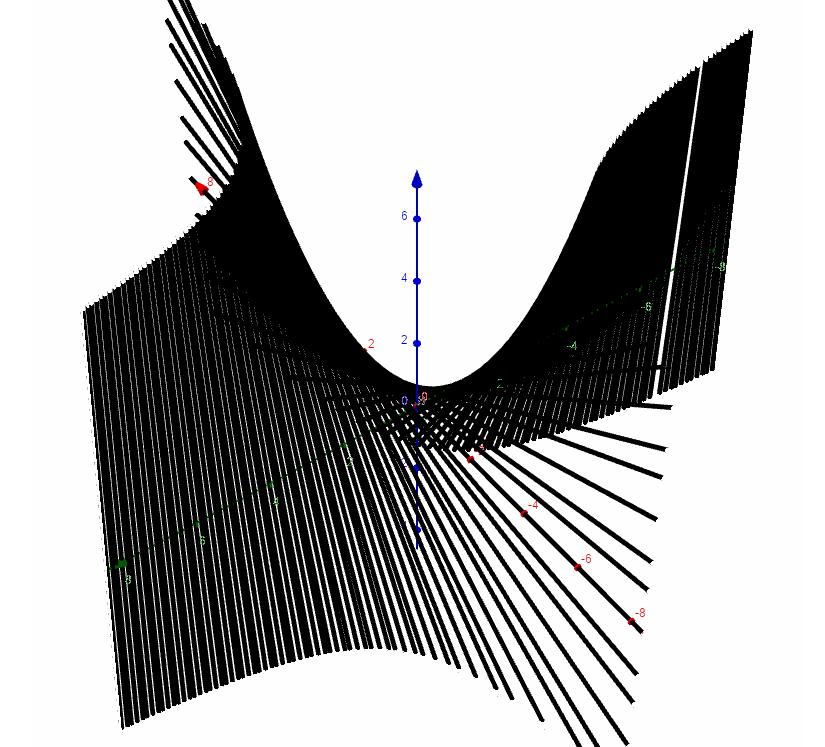
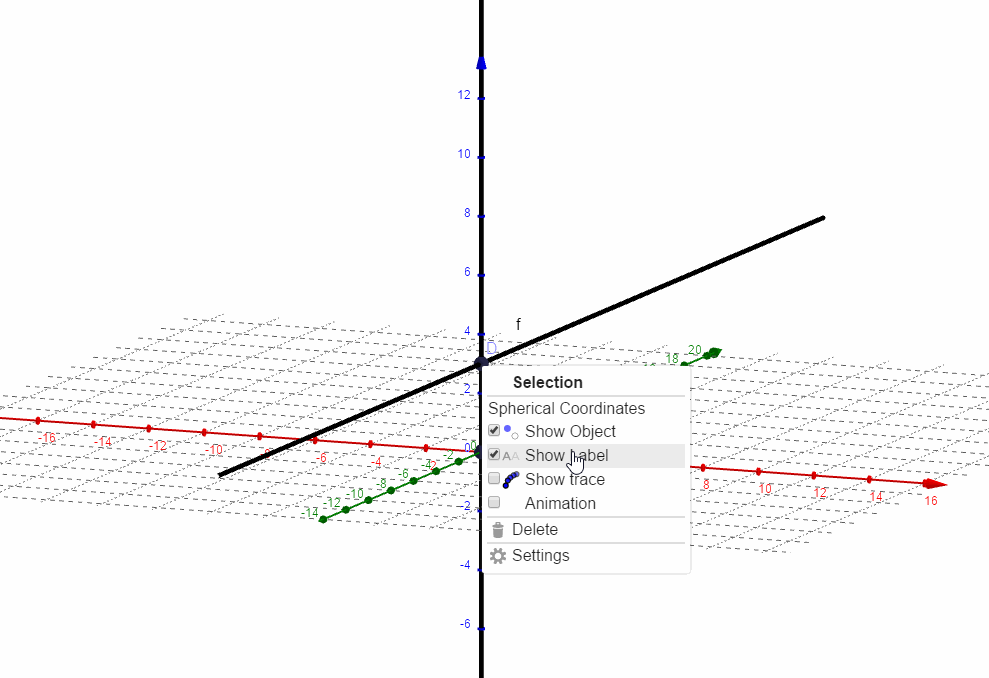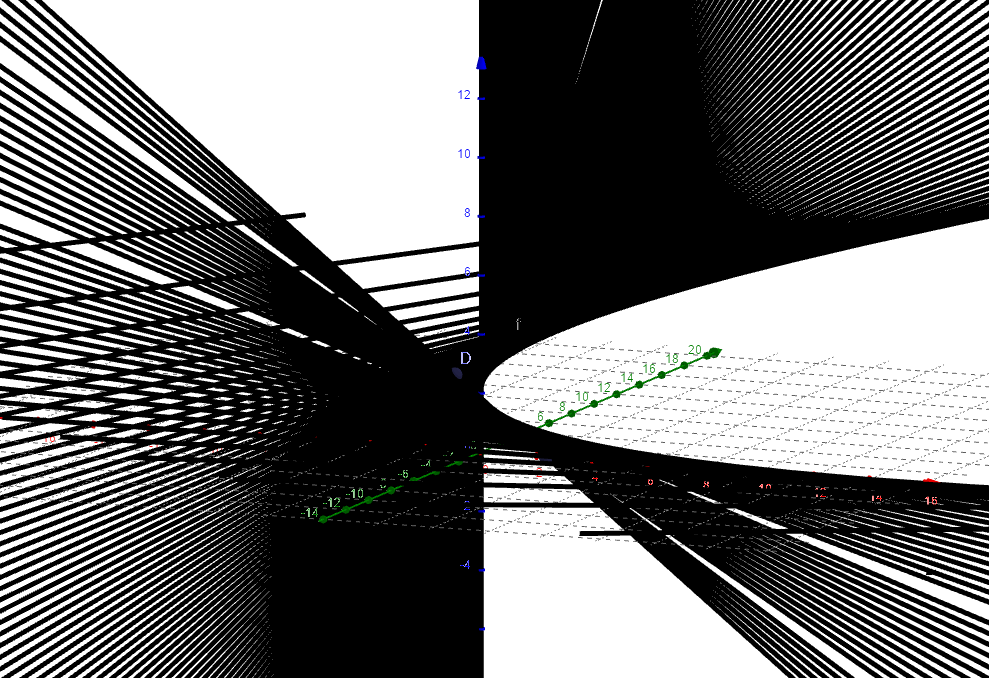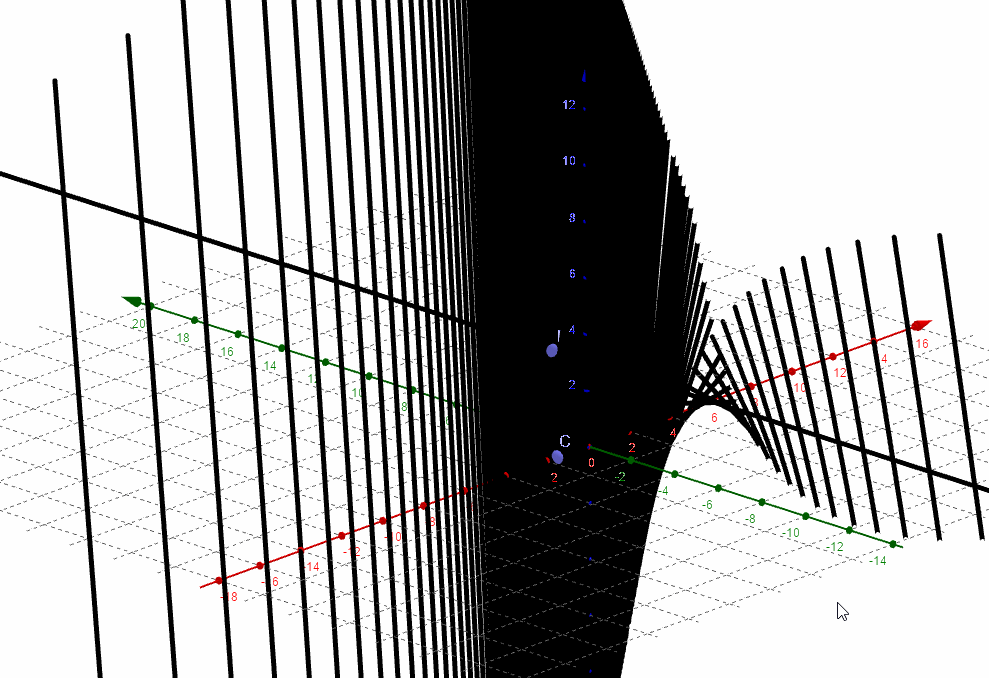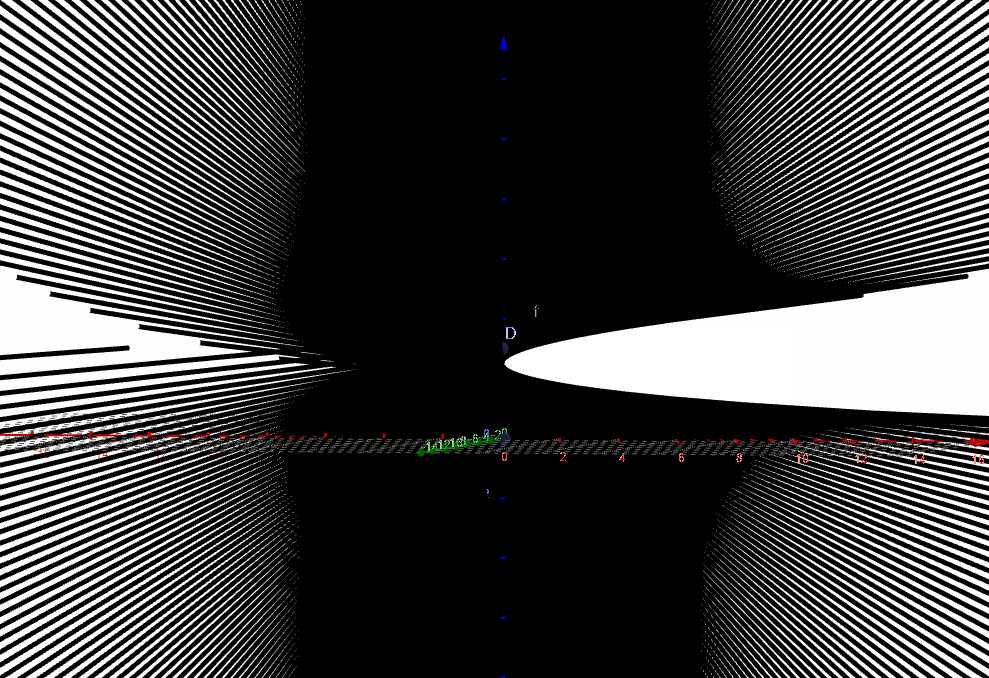
b=Curve(1,t,2t,t,-5,5)

绘制出的直线如图所示，它将作为旋转单叶双曲面的＂直纹".

通过命令：

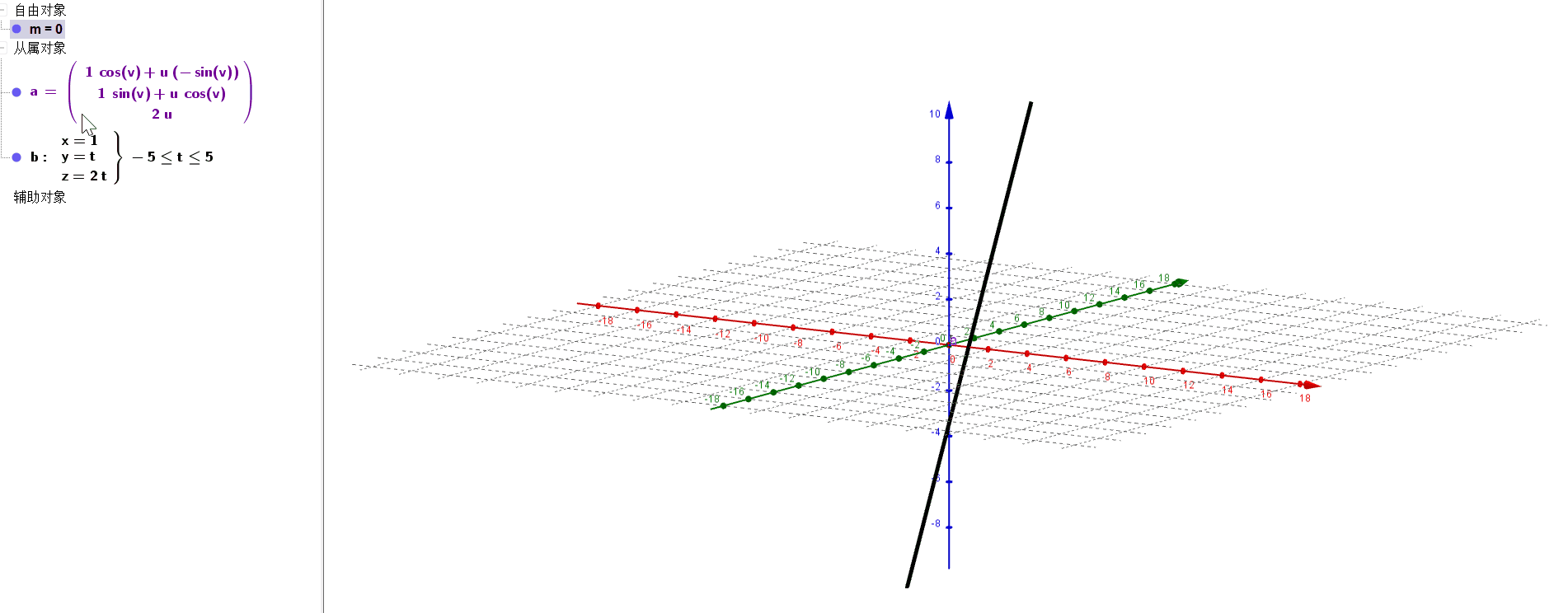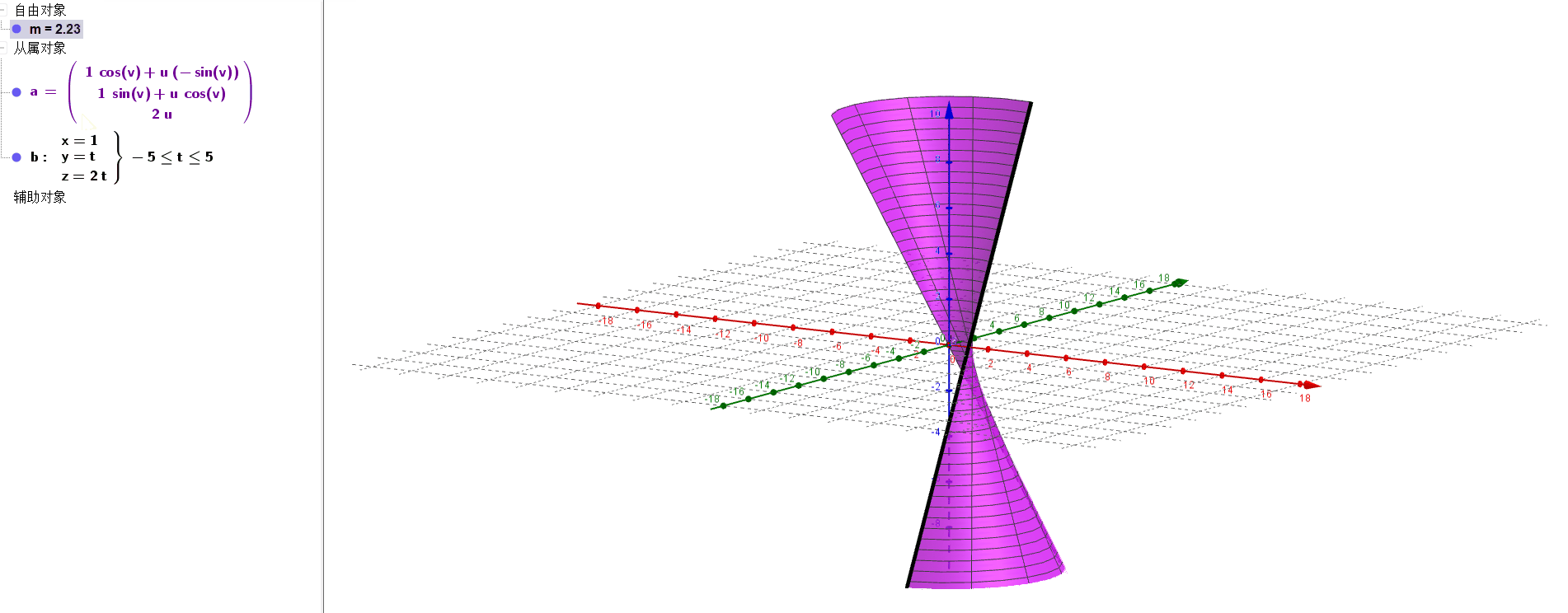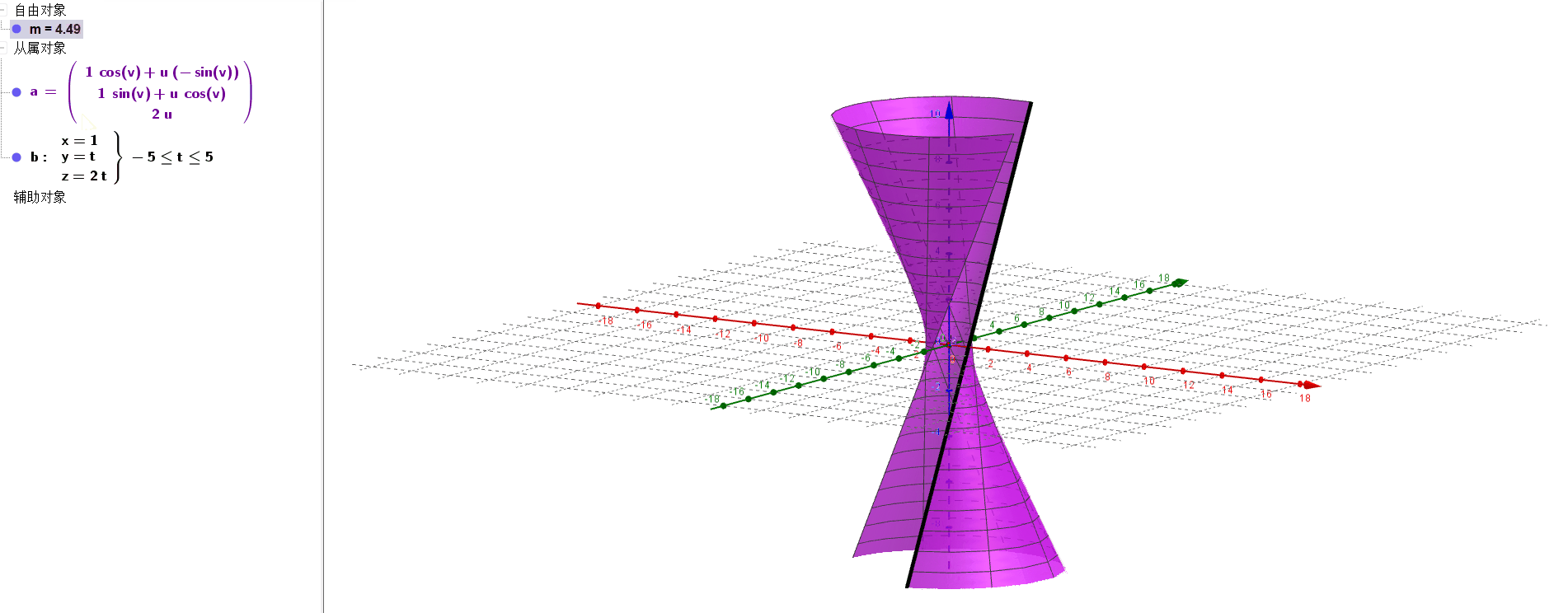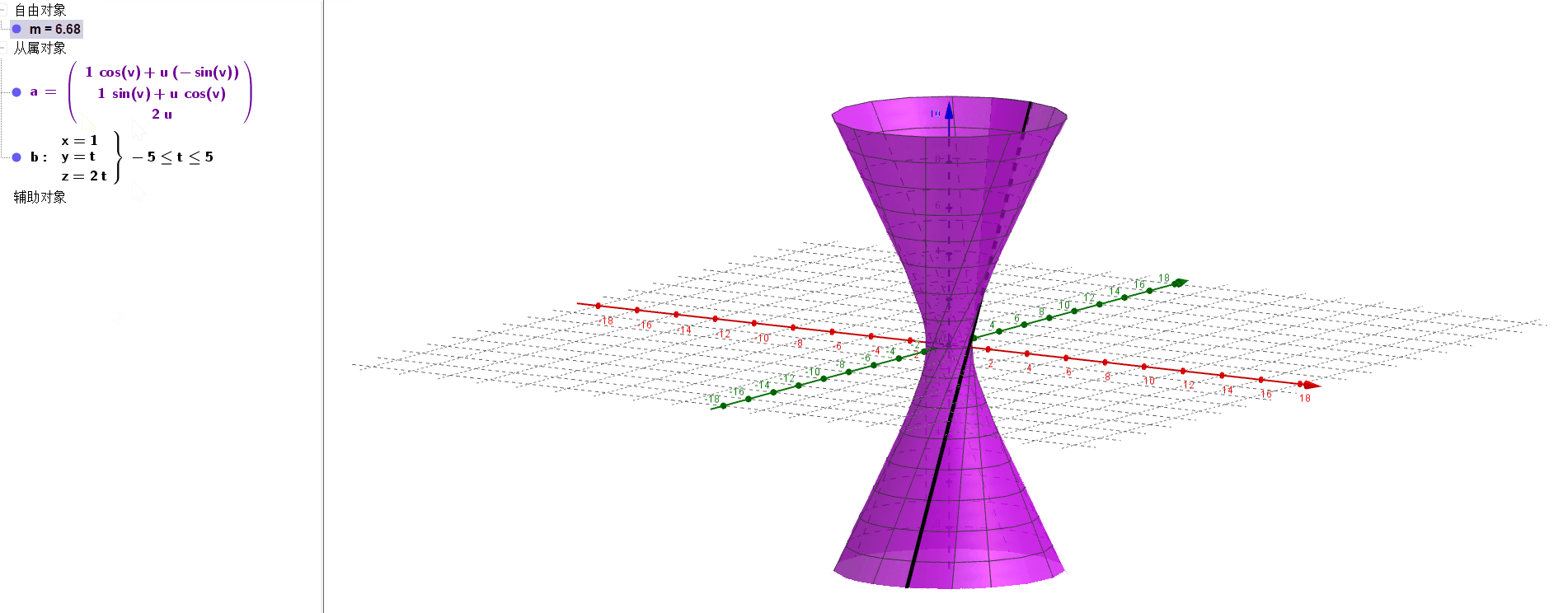
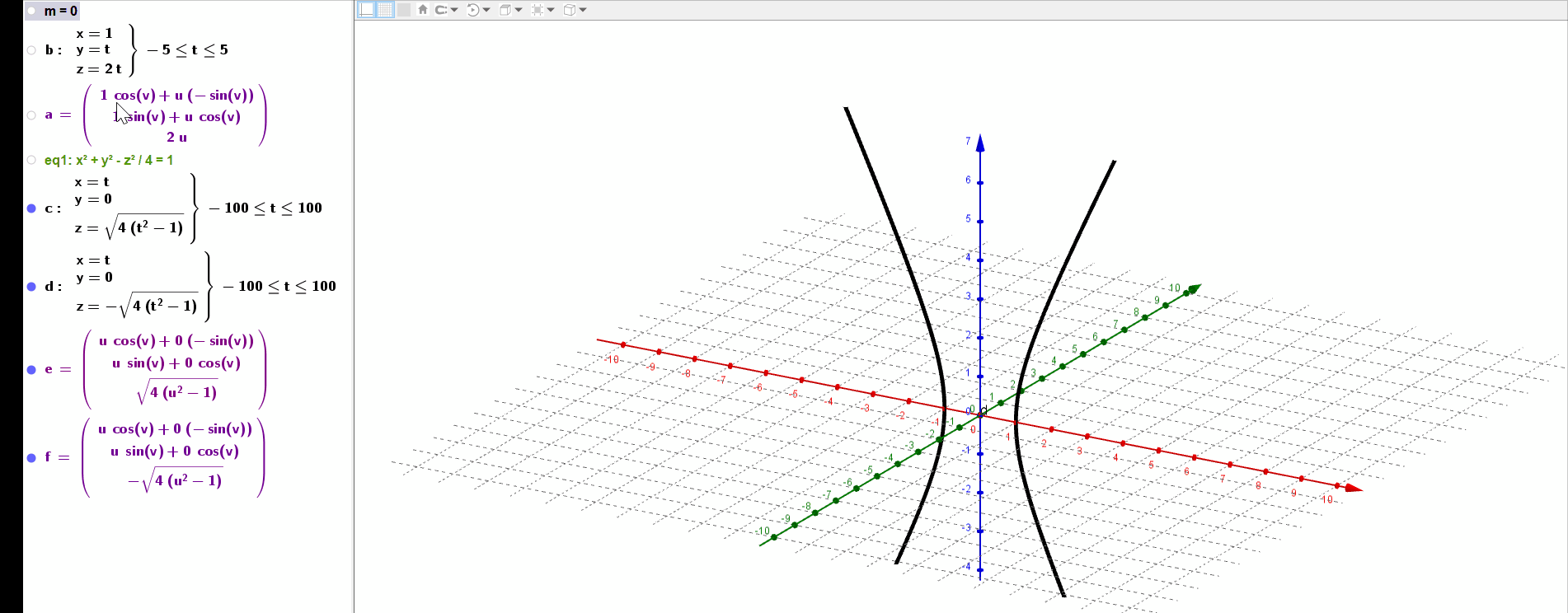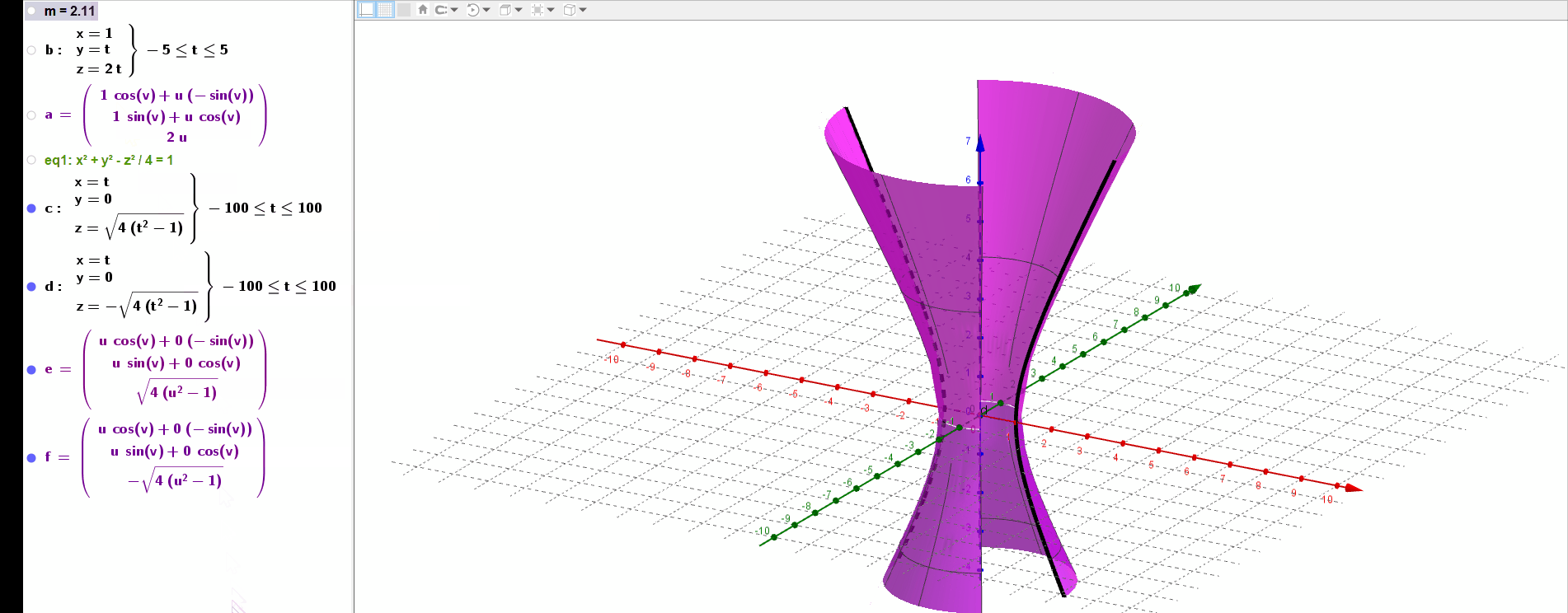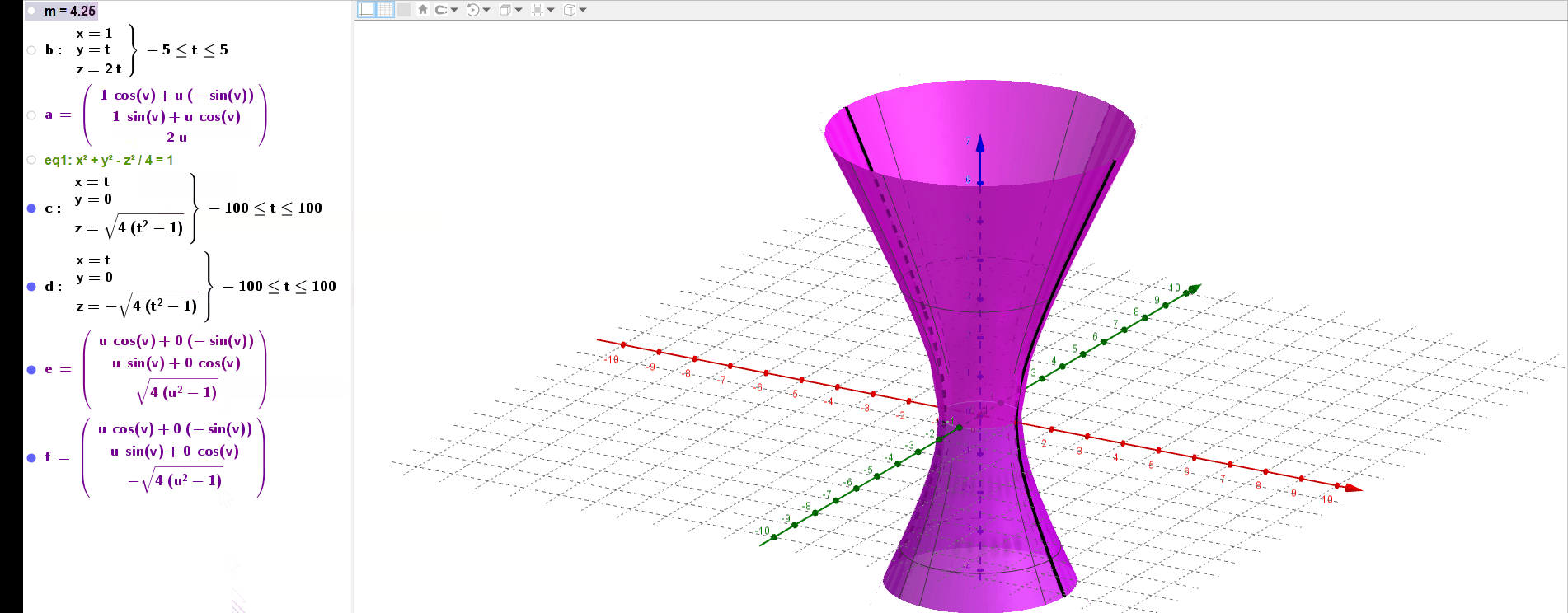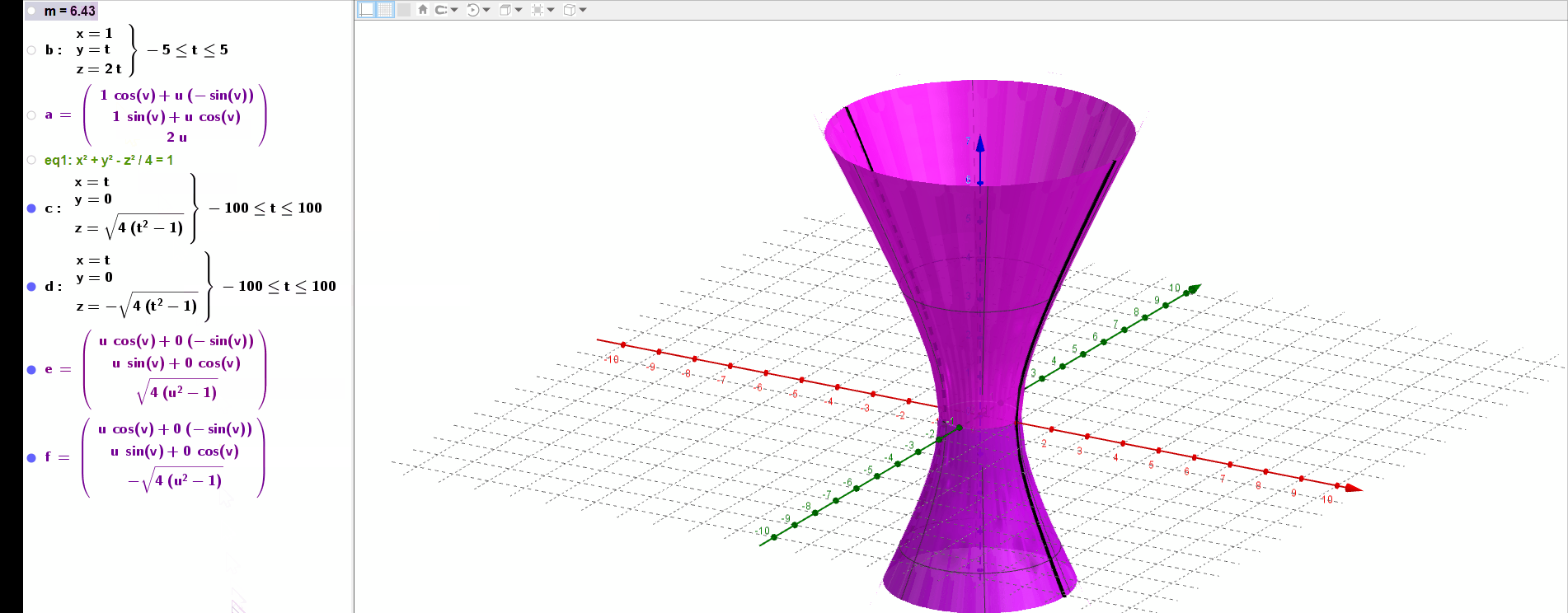
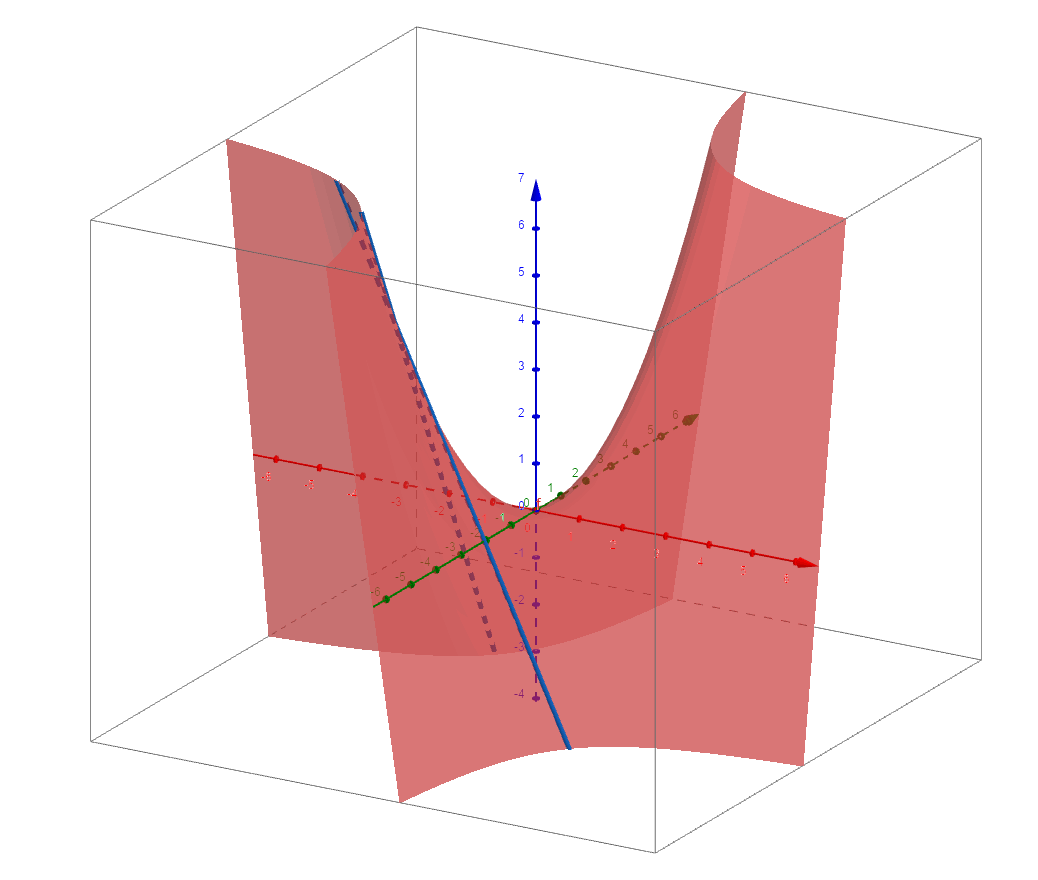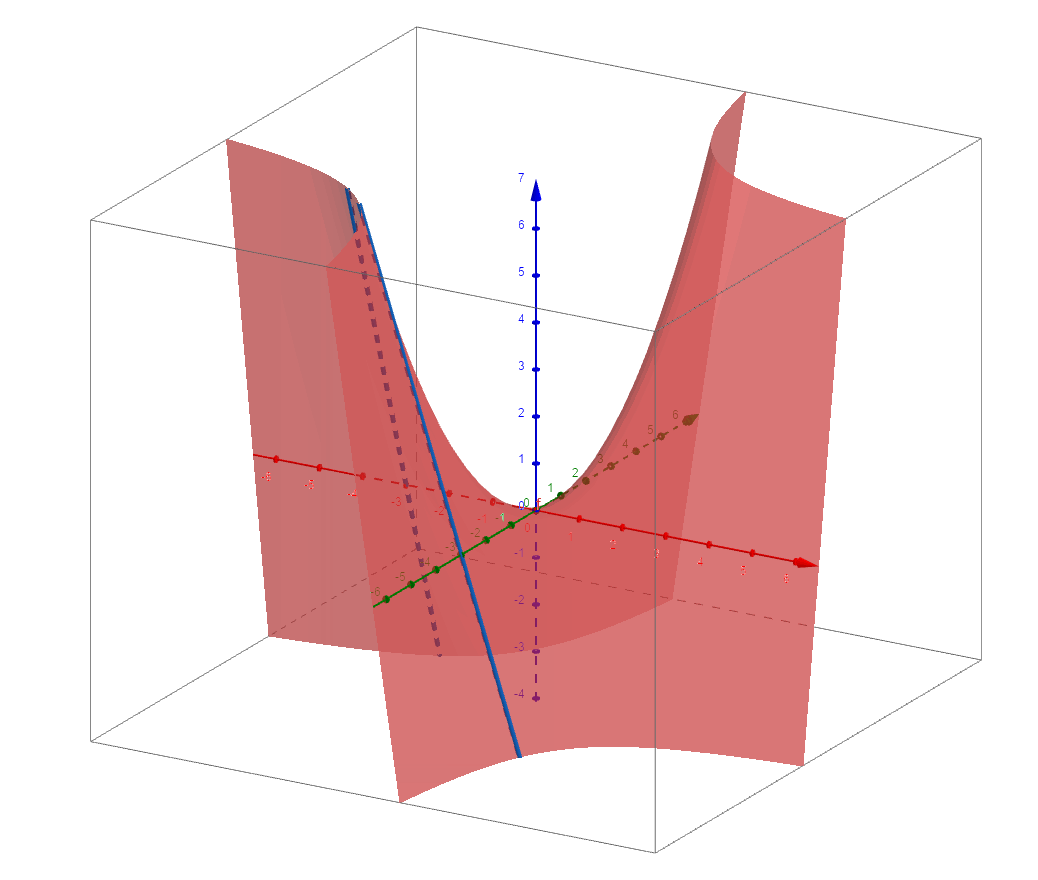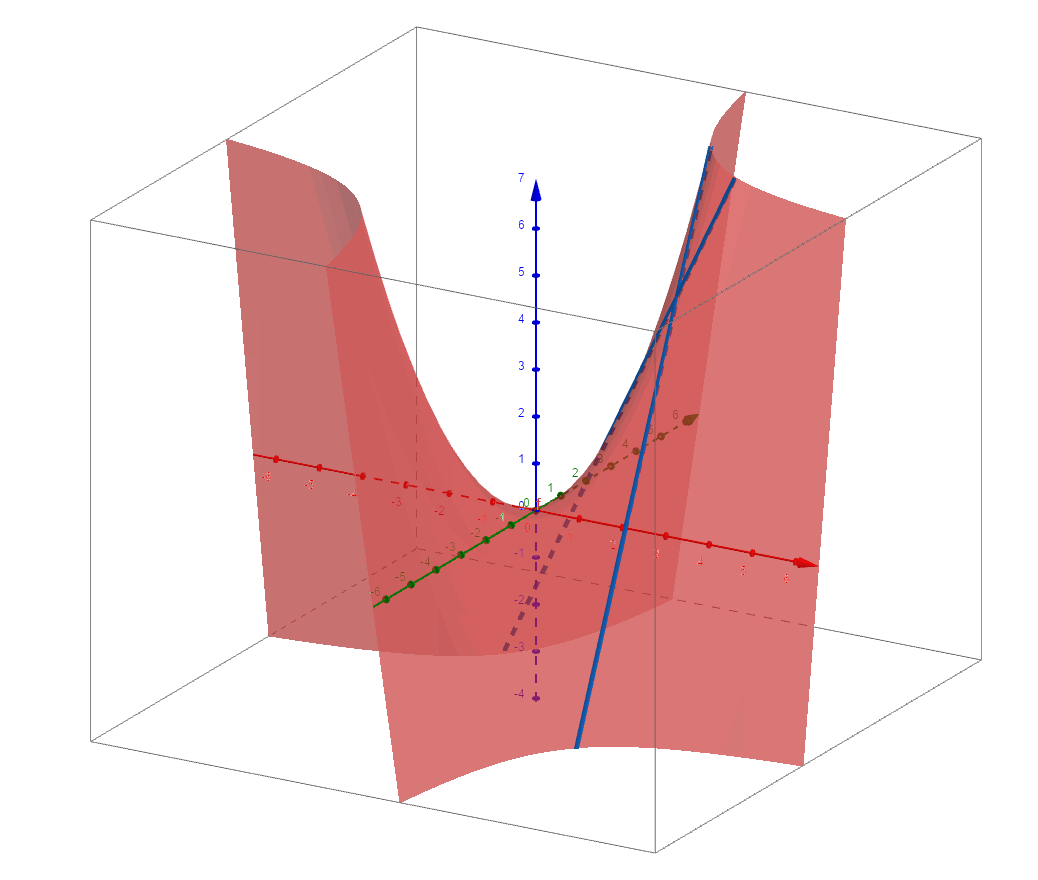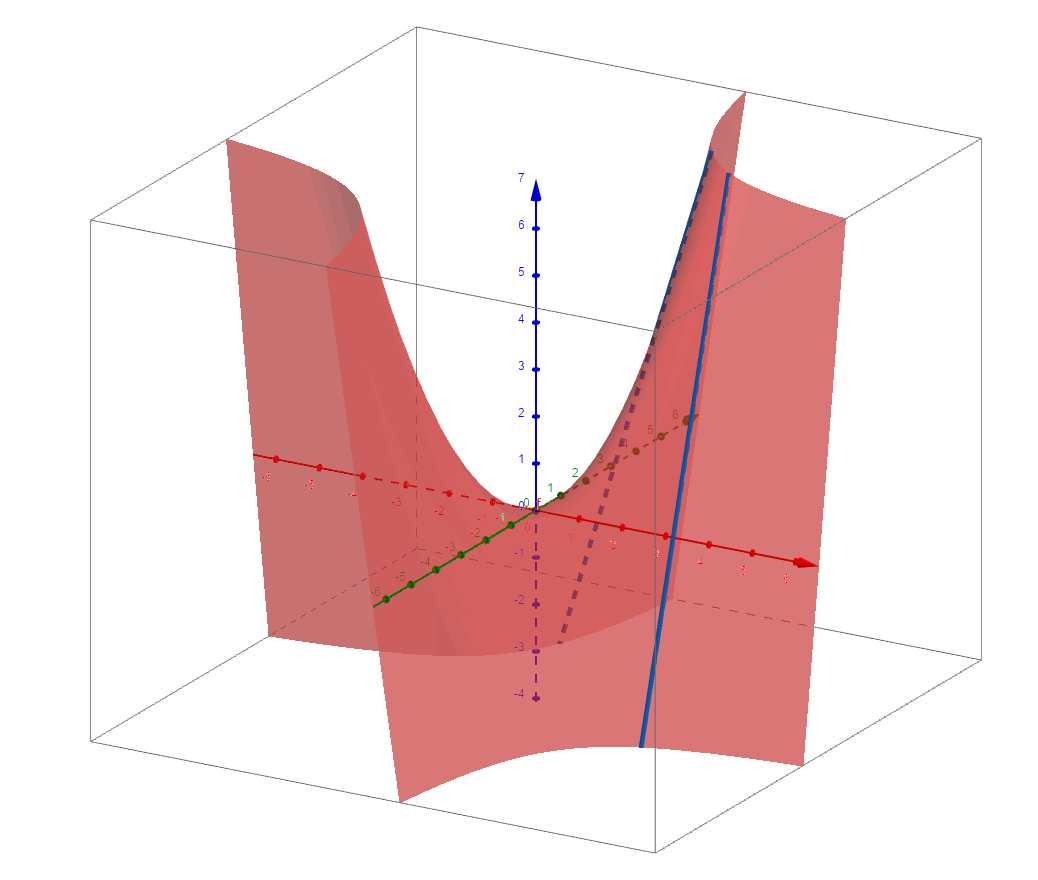
a=Surface(b,m,zAxis)

绘制曲面，命令表示直线b围绕z轴，旋转m弧度．

当m在 $[0,2\pi]$ 变化时，可以看到绘制出的曲线如下图所，性感小蛮腰：

同样的曲面可以由另一种方式构造，设 $xOz$ 坐标面上的双曲线

$\frac{x^2}{a^2}-\frac{z^2}{c^2}=1$

绕 $z$ 轴旋转一周，生成的曲面方程为：

$\frac{x^2+y^2}{a^2}-\frac{z^2}{c^2}=1$

例如，对于上面的直纹面动图，当t=0时候，直线经过

$(1,0,0)$

代入曲面方程，得到

$a=1$

$x^2+y^2-\frac{z^2}{c^2}=1$

所以，如果我们再得到曲面上的一个点，就可以算出c．

令参数方程 $t=1$ , 得到曲面经过的另一个点(1,1,2)，代入曲面方程：

$1+1-\frac{4}{c^2}=1$

得到 $c=2$

所以最终的曲面方程为：

$x^2+y^2-\frac{z^2}{4}=1$

绘制出来，可以看到它和上面两种方式绘制的直纹面完全重合．

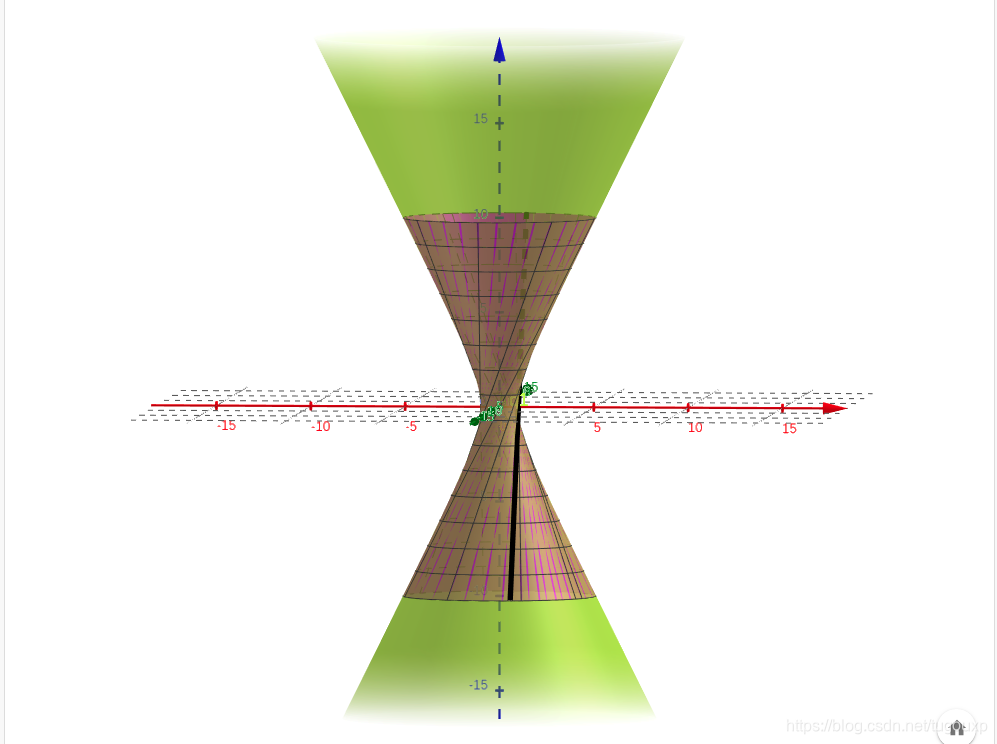
根据计算得到的曲面方程，第二种构造方式：

$\frac{x^2}{1}-\frac{z^2}{4}=1,y=0$

围绕z轴旋转，得到同一个直纹面的第二种构造方式：

大家熟悉的广州塔，就是一个旋转单叶双曲面，它是一个直纹面，在建筑时不需要弯曲钢筋，而是将其斜向排列即可，证据如下图所示，每个钢梁都是直的：

寻找规律，是不是和上面第一幅动图的绘制i过程很像？环绕的每根柱子都是直柱。

火力发电厂的冷却塔，也是做成了单叶双曲面，目的是最大利用空气流动来提高冷却的效率。

大屯发电厂外景，冷却塔主题。

机械中的应用

设计转动轴不互相平行的转动轴：

2.马鞍面

经典的马鞍面要属方程

$z=xy$

表示的双曲抛物面了,它的图形是下面这个样子的：

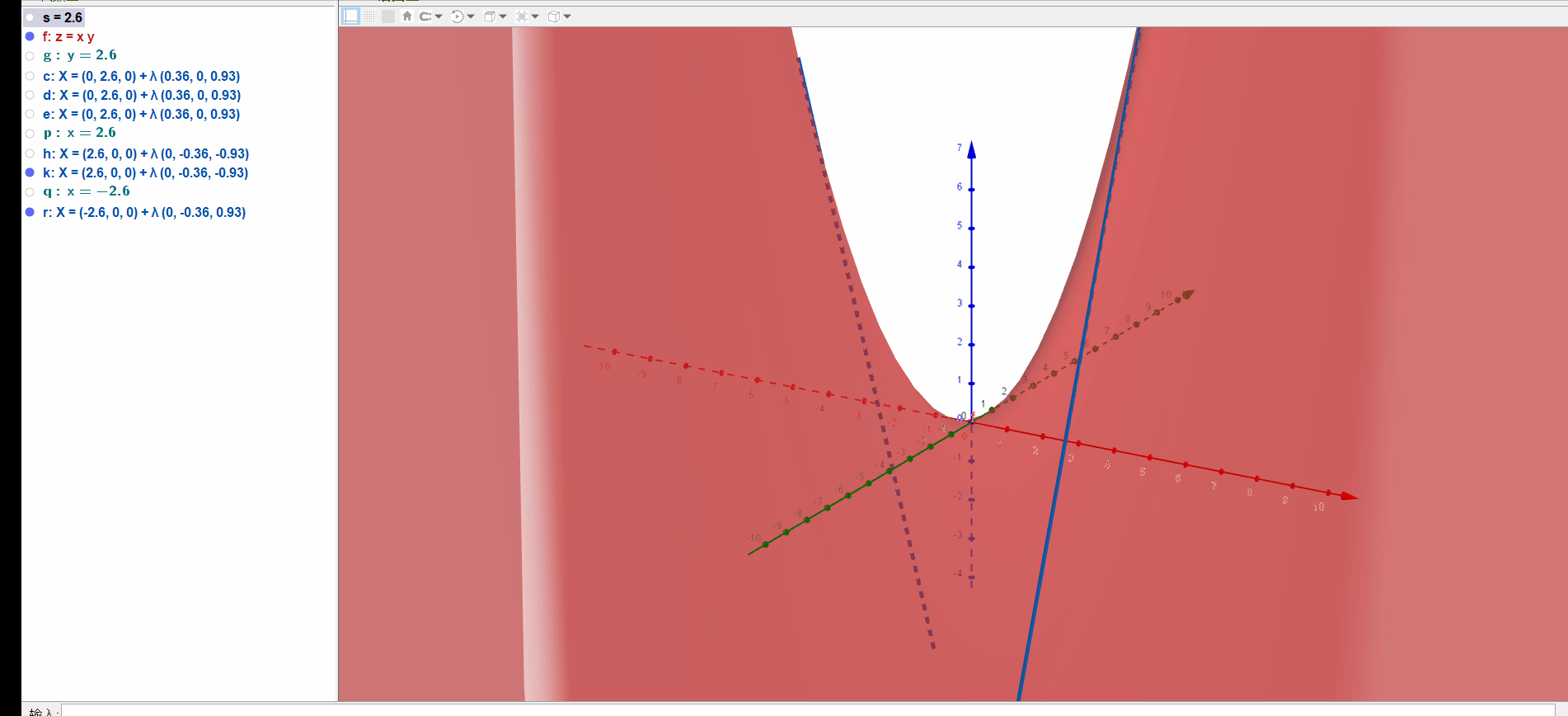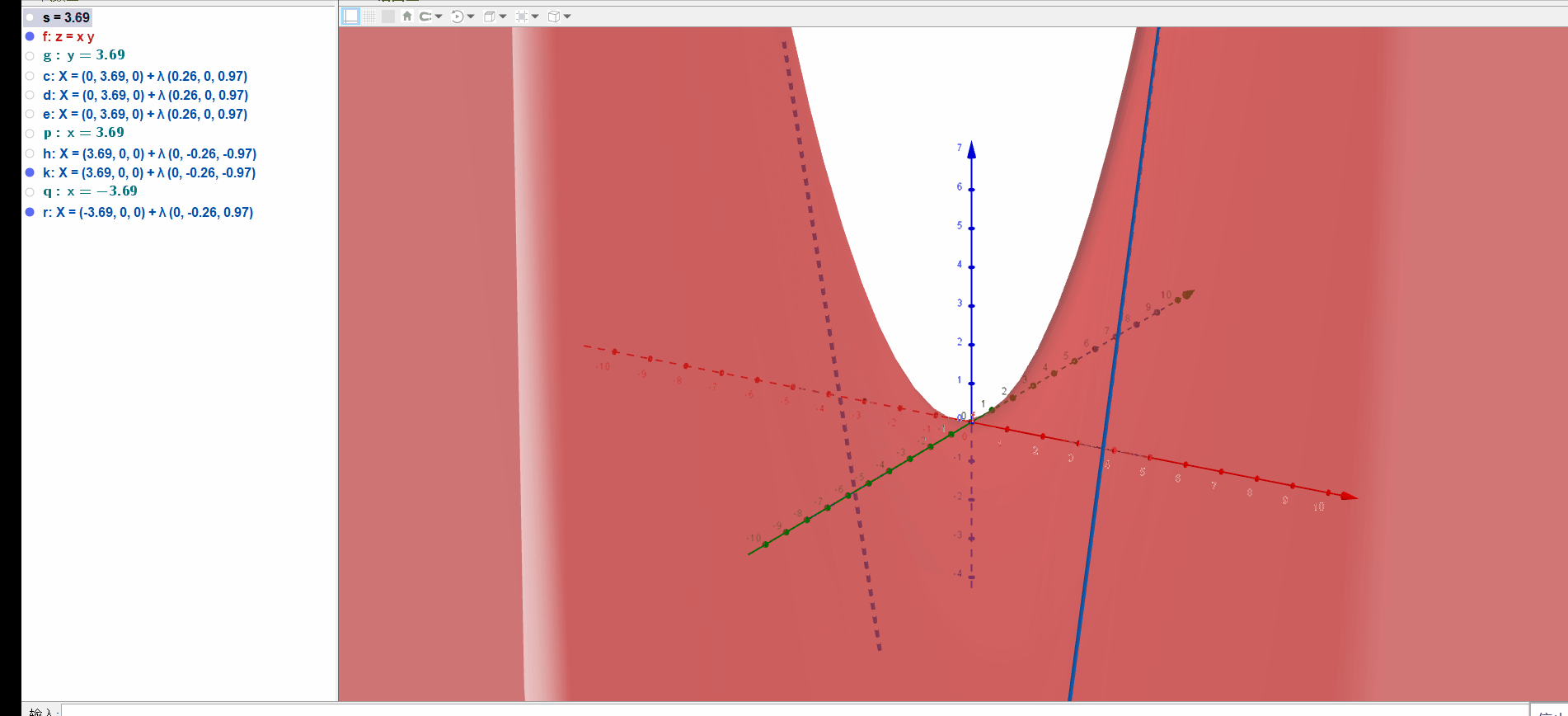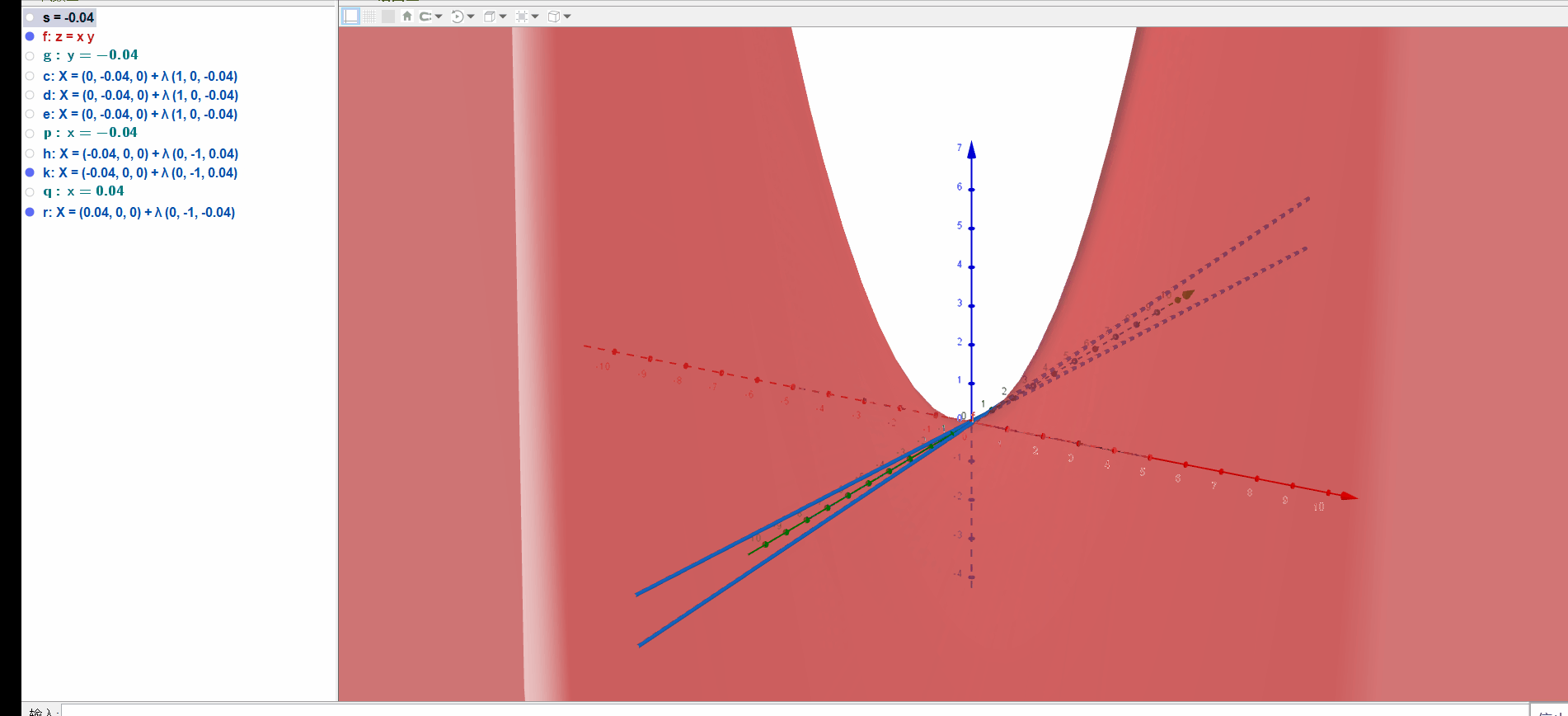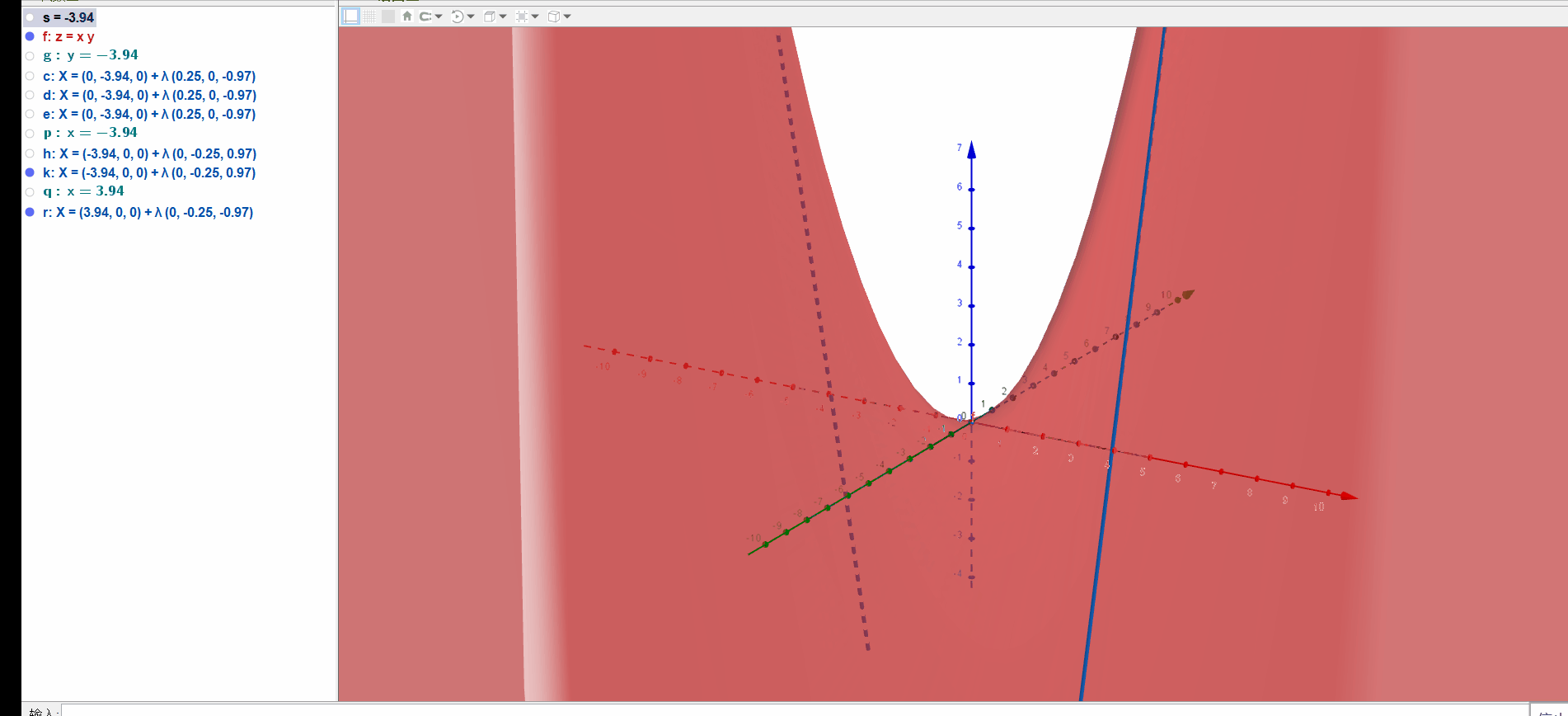
它也是一个直纹面，直接看可能看不出来，我们可以先找一些特殊位置，比如坐标轴，坐标轴是直的，看上去也再平面上，俯视图如下:

实际上，如果用法向量分别为(0,1,0)和（1,0,0)的平面去截曲面，得到的截线即是直线:

可以试着推一下截线的方程：

对于法向量 $\vec{n}=[0,1,0]$ ，通过一点 $(x_0, y_0, z_0)$

根据点法式得到平面方程为：

$0\cdot (x-x_0)+1\cdot (y-y_0)+0\cdot(z-z_0)=0$

也就是平面

$y=y_0$

它与x轴的交点是

$[0,y_0,0]$

联立

$\left\{\begin{matrix} z=xy\\ y=y_0 \end{matrix}\right.=>\left\{\begin{matrix} x=t\\ y=y_0\\ z=y_0t \end{matrix}\right.$

所以，直线为经过 $[0,y_0,0]$ ,且方向向量为: $[1,0,y_0]$ 的直线。

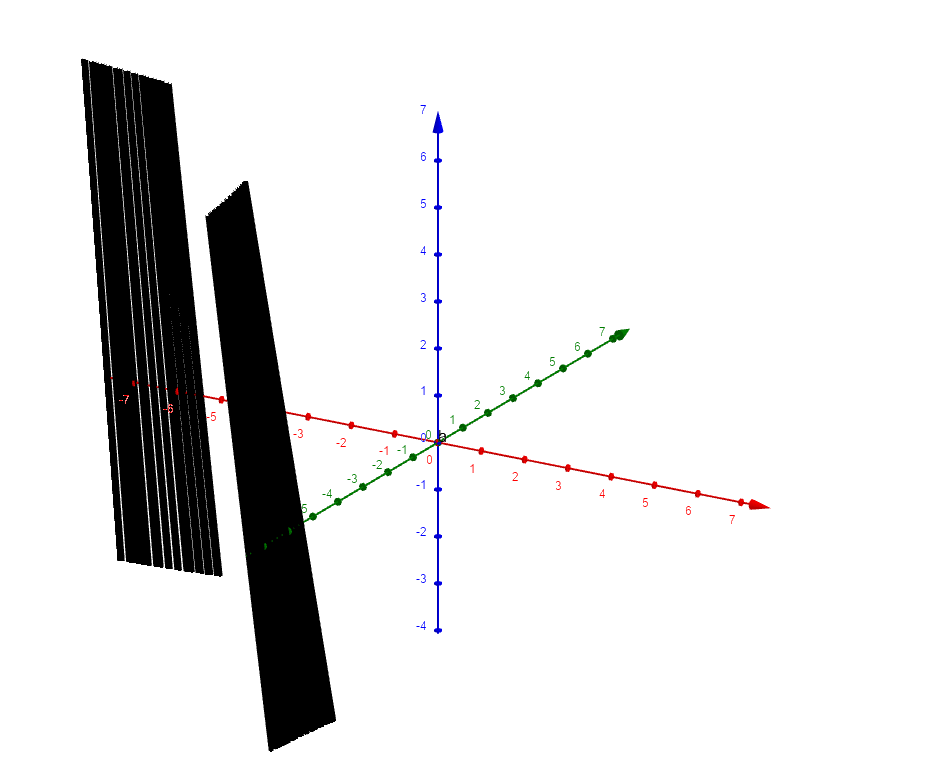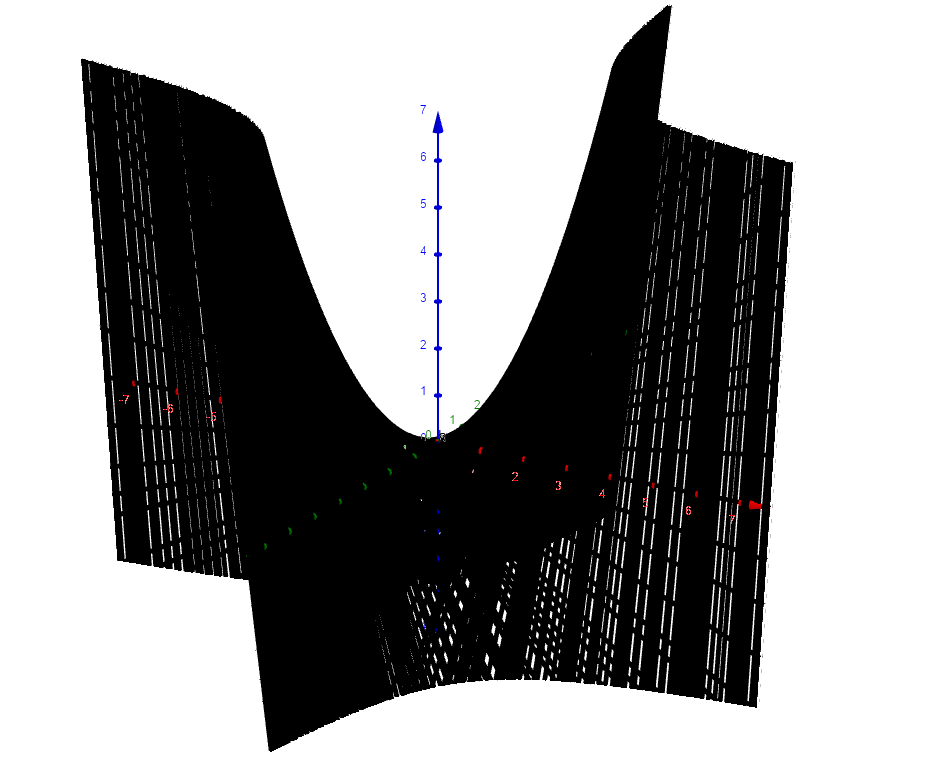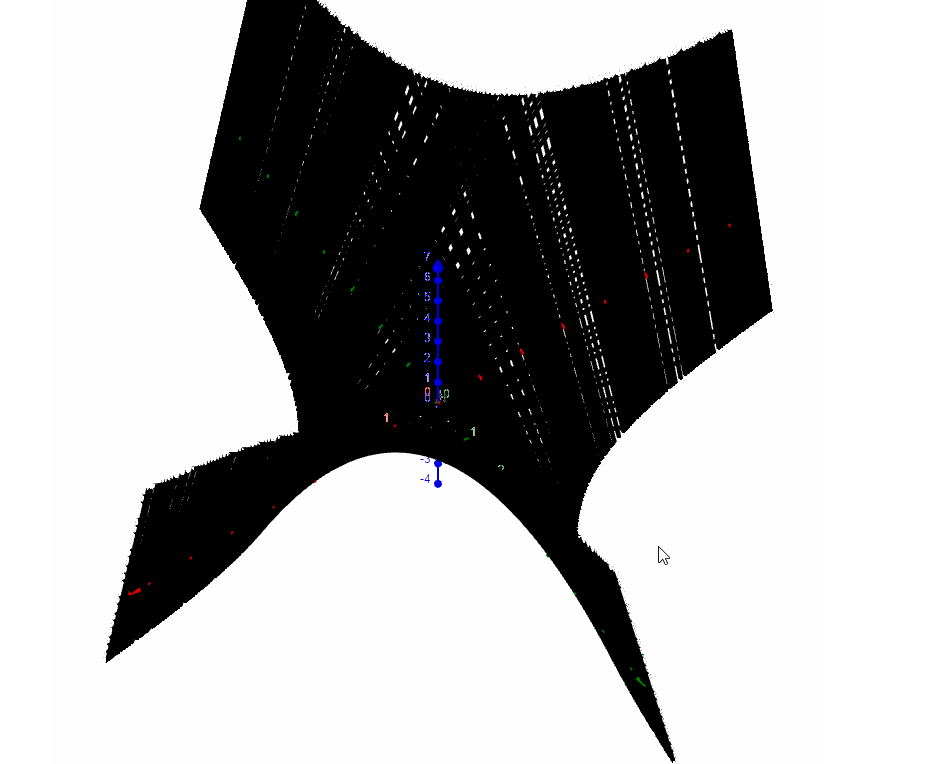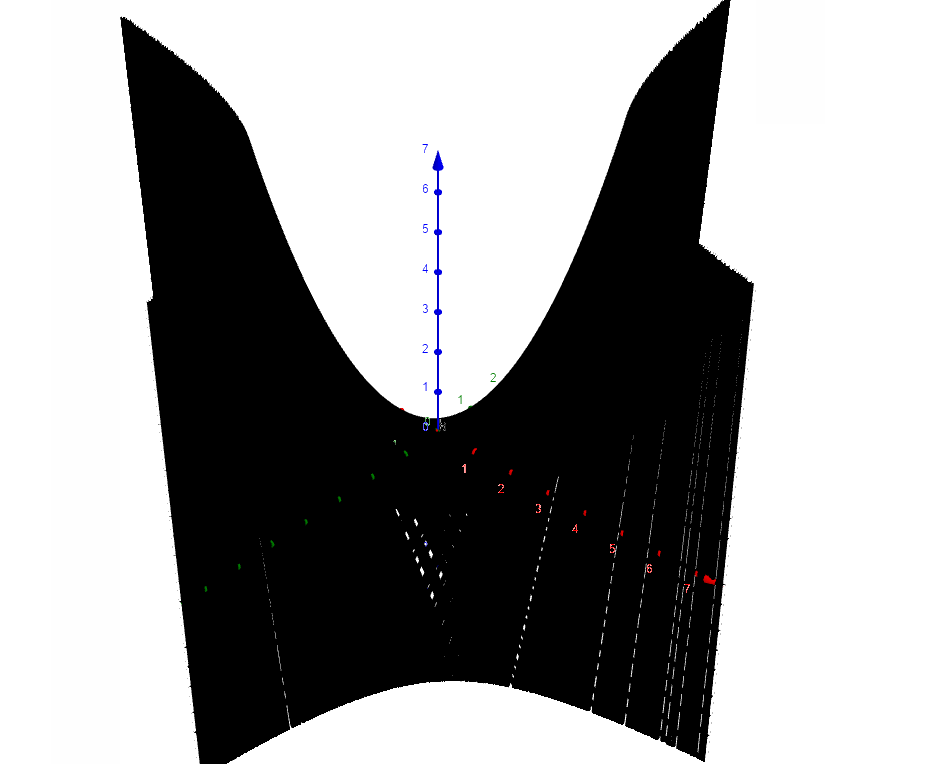
使用命令

a=Curve(t,n,n t,t,-10,10)

绘制直线，并让直线动起来，观察扫出区域的形状：

对于法向量 $\vec{n}=[1,0,0]$ ，通过一点 $(x_0, y_0, z_0)$

根据点法式得到平面方程为：

$1\cdot (x-x_0)+0\cdot (y-y_0)+0\cdot(z-z_0)=0$

也就是平面

$x=x_0$

它与x轴的交点是

$[x_0,0,0]$

联立

$\left\{\begin{matrix} z=xy\\ x=x_0 \end{matrix}\right.=>\left\{\begin{matrix} x=x_0\\ y=t\\ z=x_0t \end{matrix}\right.$

所以，直线为经过 $[x_0,0,0]$ ,且方向向量为: $[0,1,x_0]$ 的直线。

a=Curve(t,n,n t,t,-10,10)

两根母线一起绘制，图形更漂亮：

第三种构造方式：

直线f通过z轴并平行于绿色的y轴，动点C位于原点，初始状态如下图，连线CD垂直于翼面直线l和xAxis的方向平面。

在上图的初始状态下，让动点c,d同时开始运动，扫过的区域构成马鞍面：

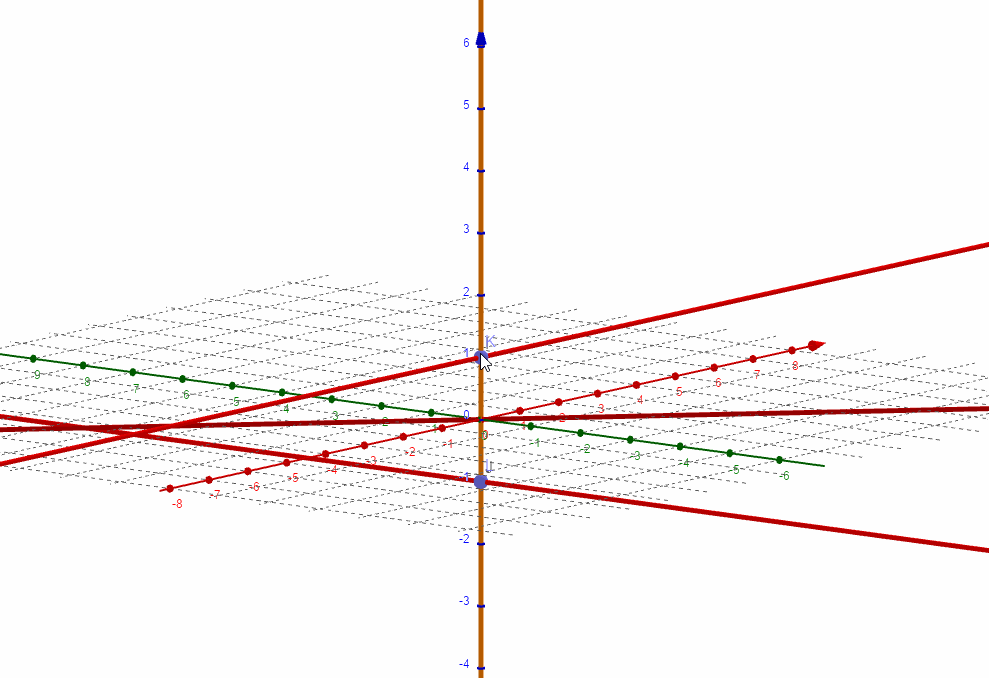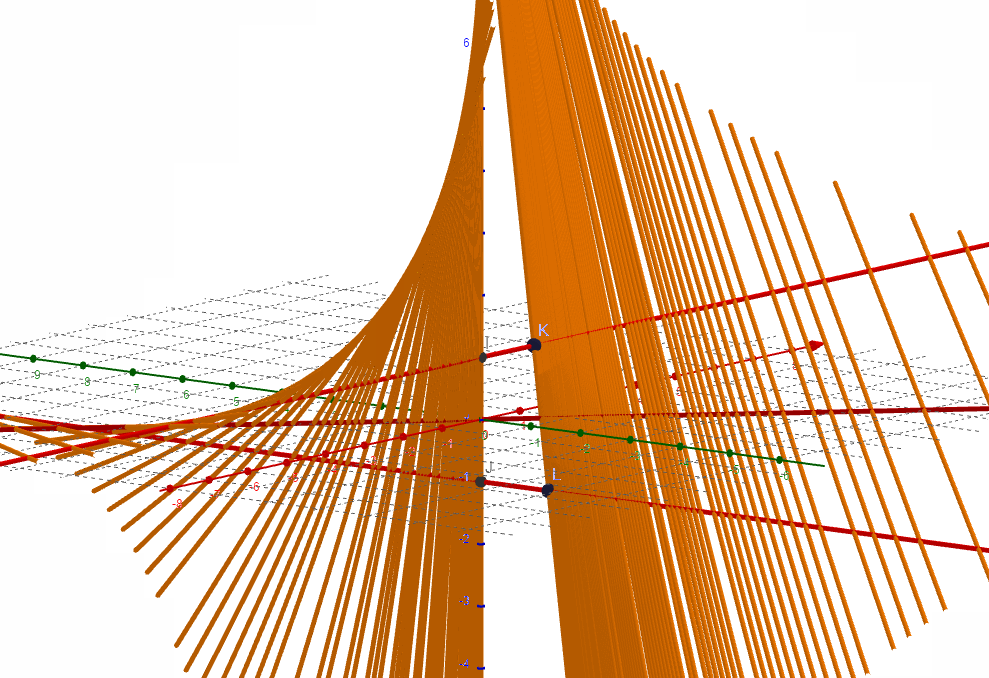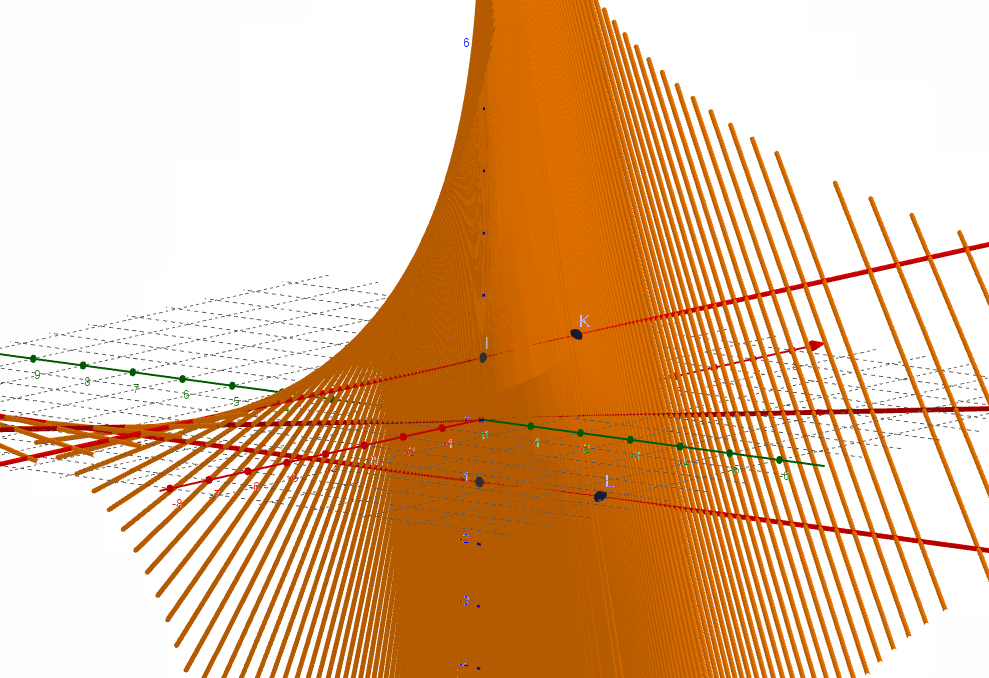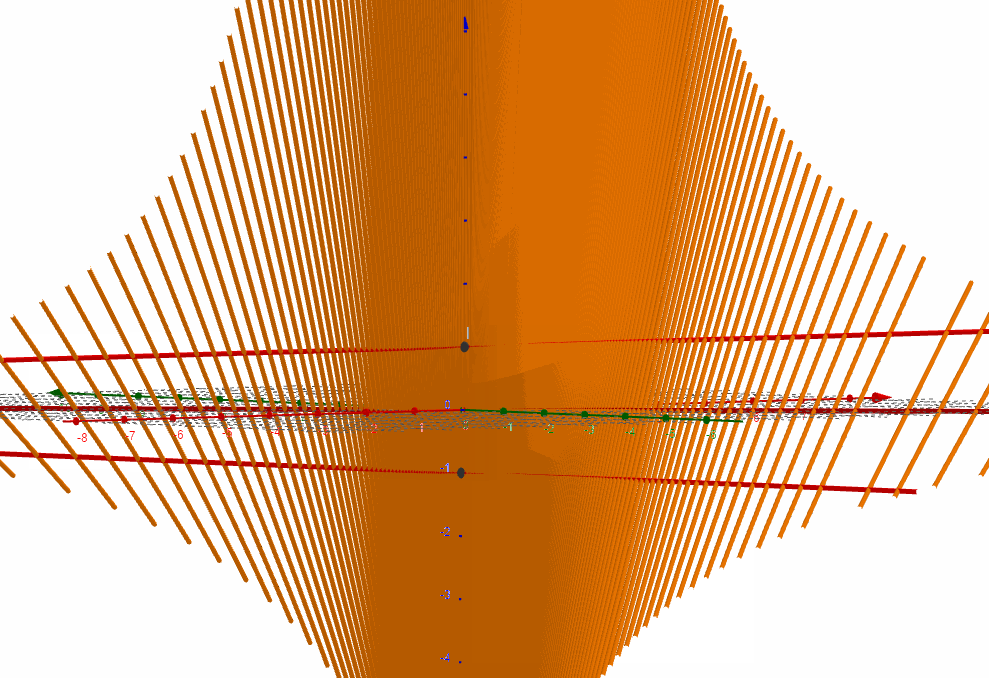
为了把马鞍面的形状讲透，我们反过来，看实际的马鞍面上是否找到上图所示的两条异面直线，很好找，看下图：

这样的运动方式，两条动直线总有互相垂直的时刻。

我们把垂直时刻的位置抓出来，此时两条互相垂直的异面直线都是马鞍面上的直纹。它们的方向向量分别是 $(0,-0.71,0.71)$ 和 $(0,-0.71,-0.71)$

构造两条异面直线之间的公垂线，让它动起来：

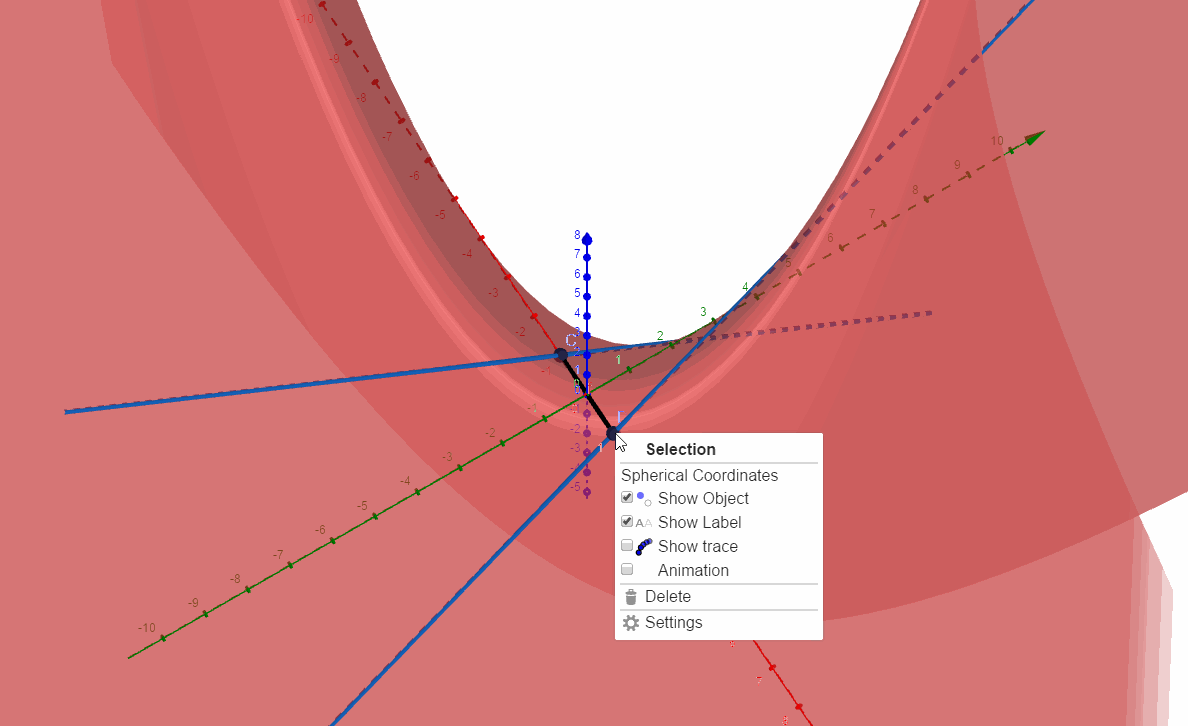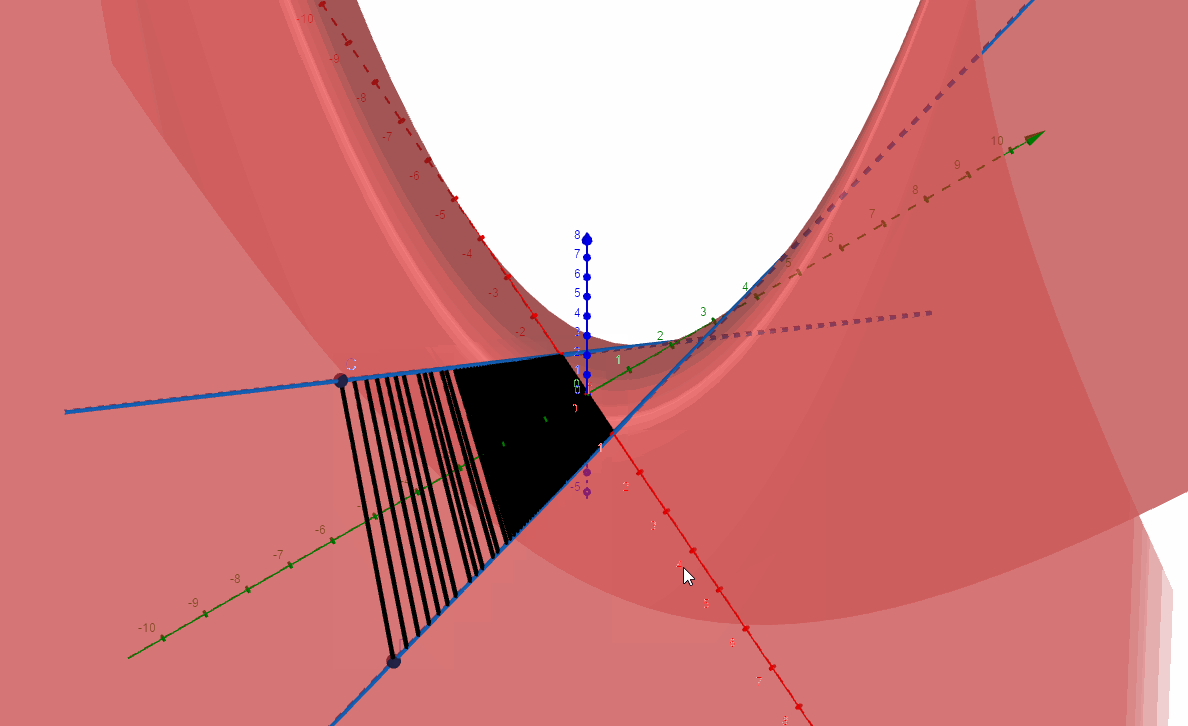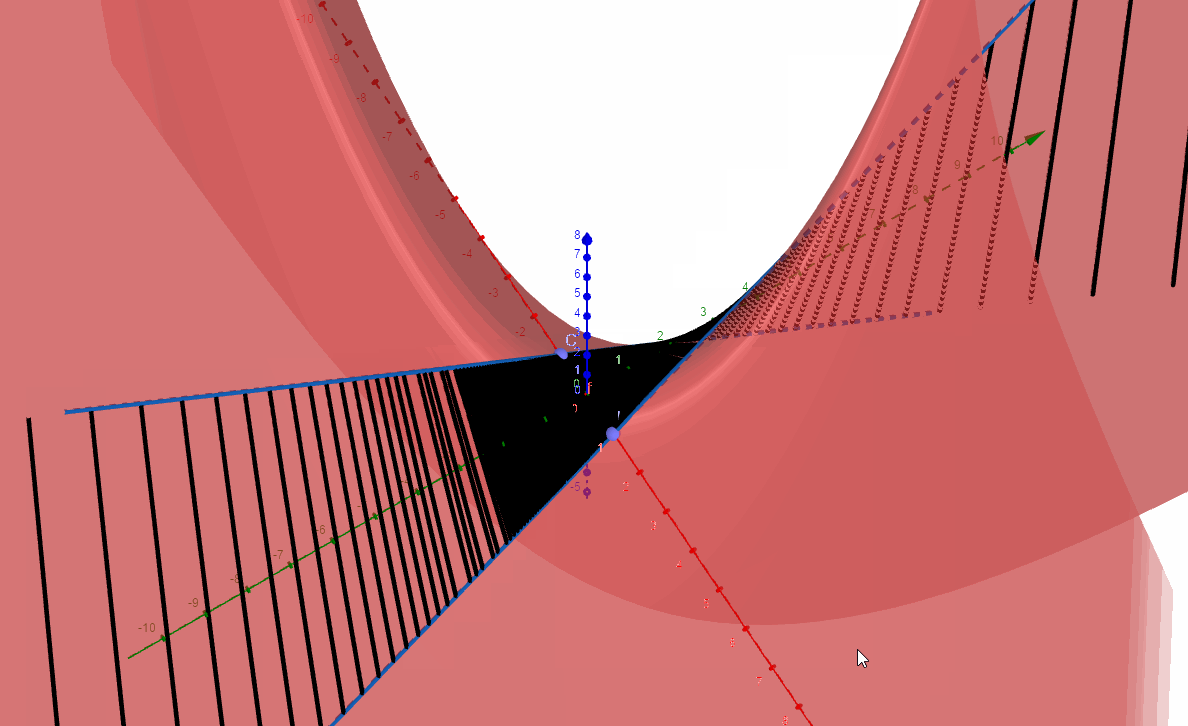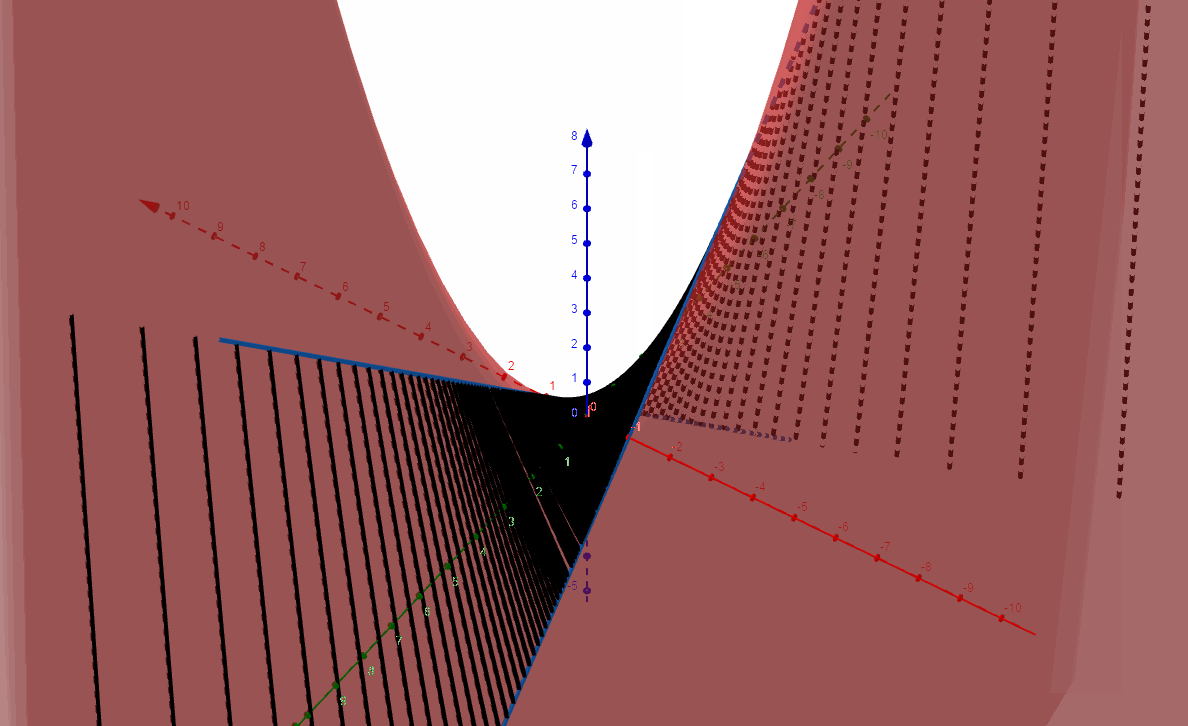
动线段扫除的轨迹完全贴合原来的马鞍面，所以可以看出，互相垂直的异面直线方式构造马鞍面也是可以的。

受到神经网络里面经常用的sigmoid激活函数的启发，想到另一种构造类马鞍面的方式：

sigmoid函数的图形如下：

稍微修改一下，将其值域变为 $[-\pi/2, \pi/2]$ ，函数为：

$f(x)=\pi(\frac{1}{1+e^{-x}}-\frac{1}{2})$

在三维空间中，构造两个点：

$A(a, 0, 0)$

和

$B(a, cos\bigg[\pi(\frac{1}{1+e^{-x}}-\frac{1}{2})\bigg], sin[\pi(\frac{1}{1+e^{-x}}-\frac{1}{2})\bigg])$

构造直线AB, 则AB为从负无穷处到正无穷处旋转180度的直线，它扫过的轨迹非常像马鞍面，究竟是不是我不知道，需要证明。

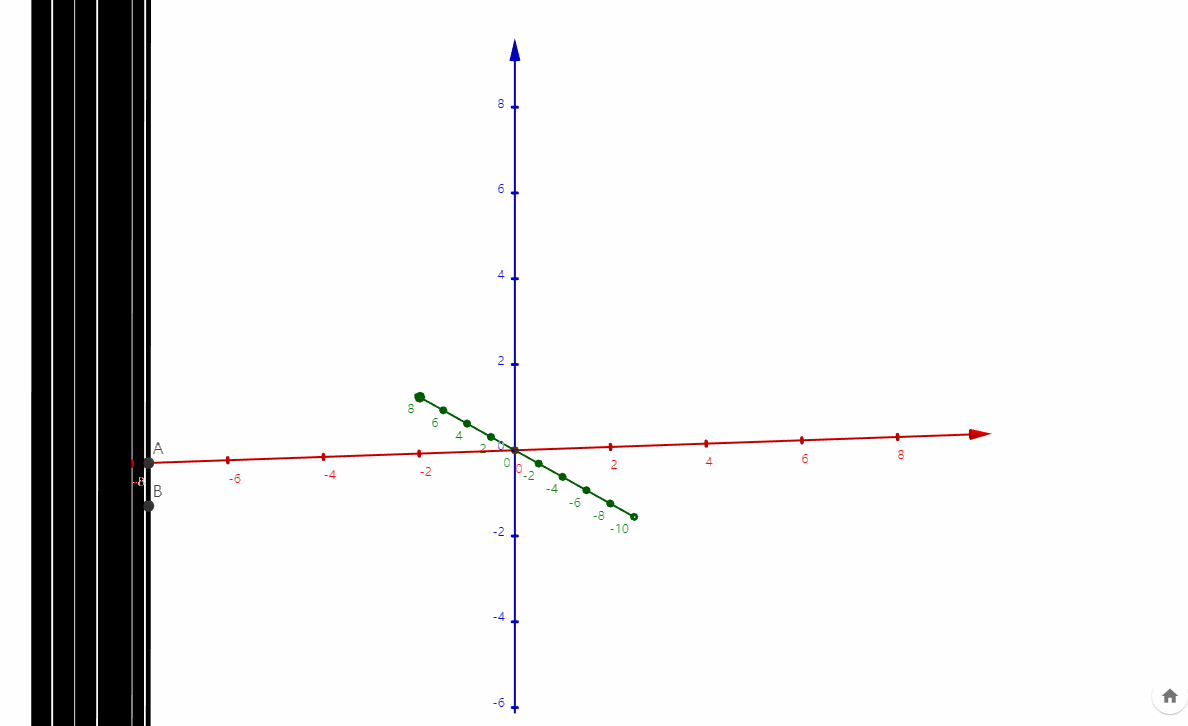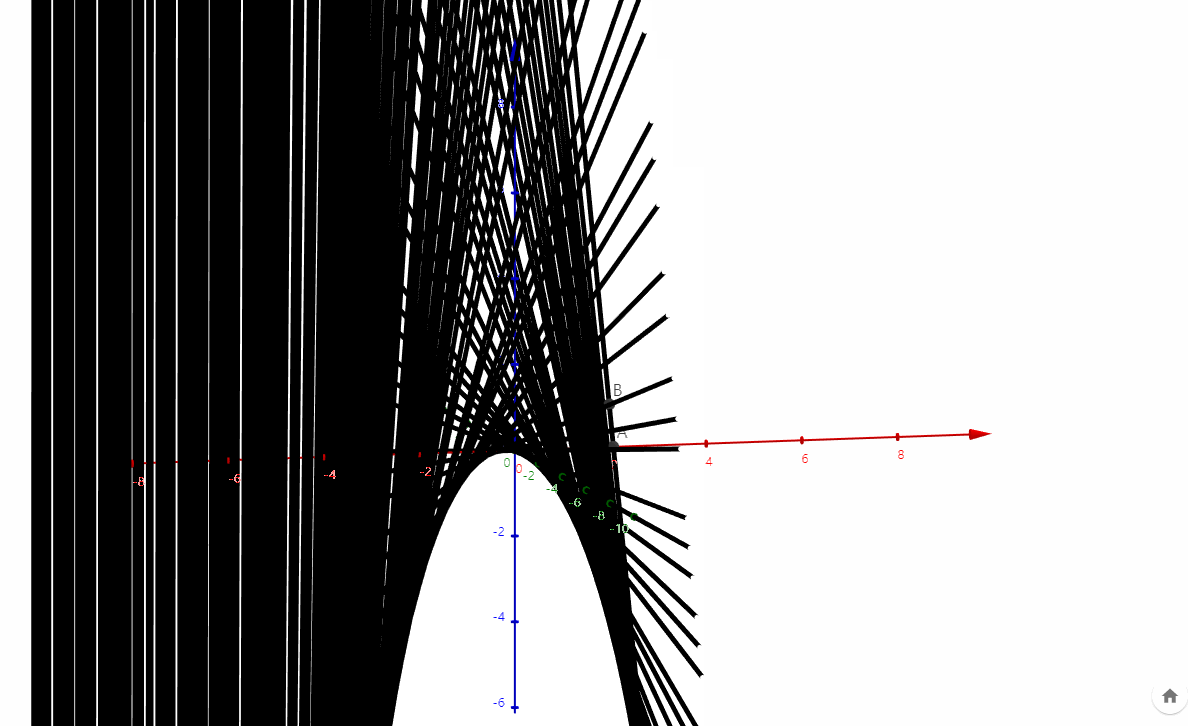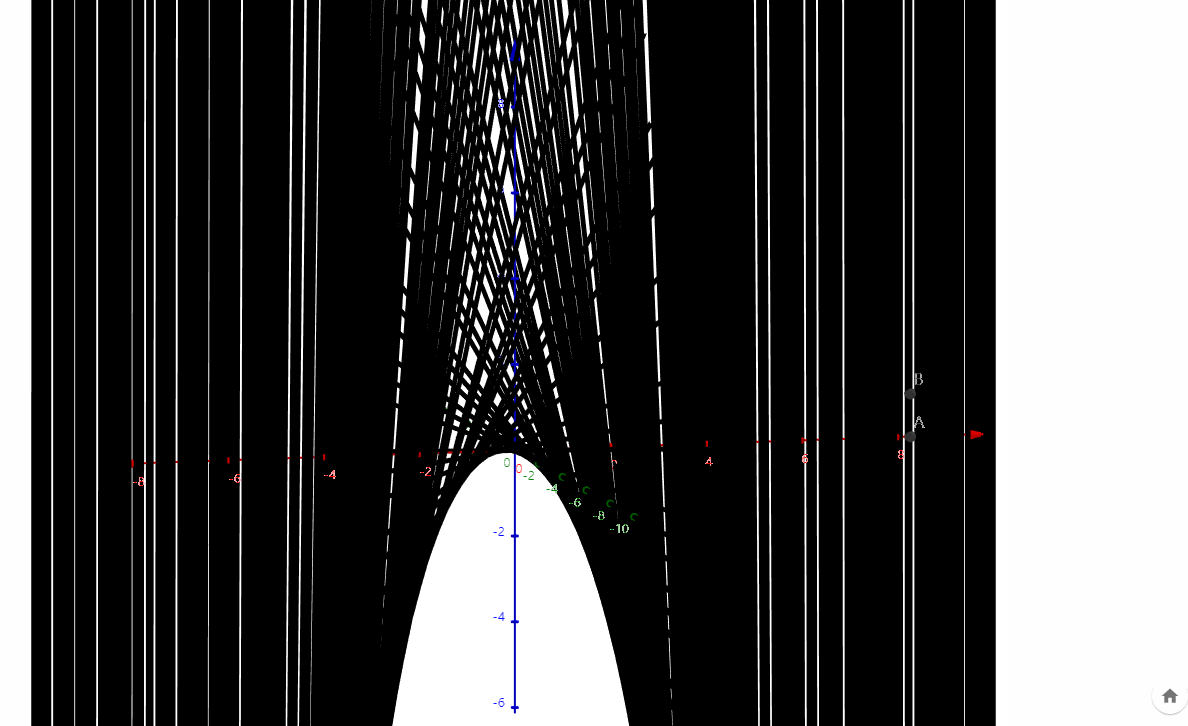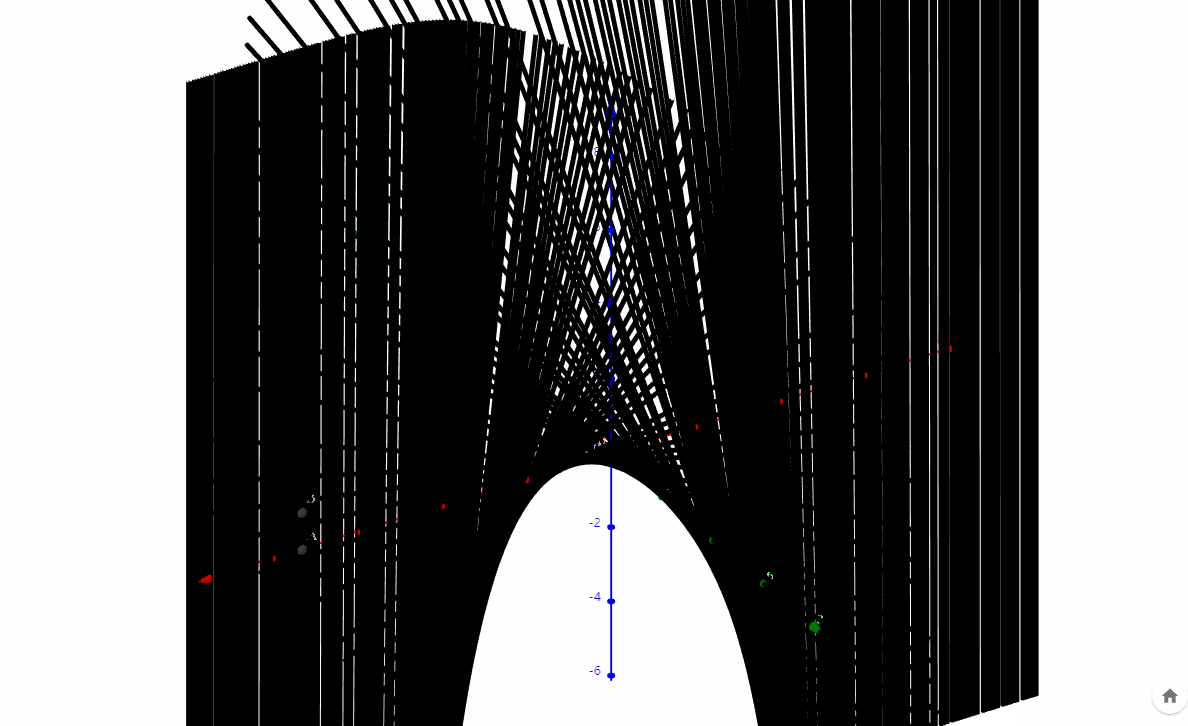
马鞍面学名叫做双曲抛物面，在经济学中有很重要的应用。

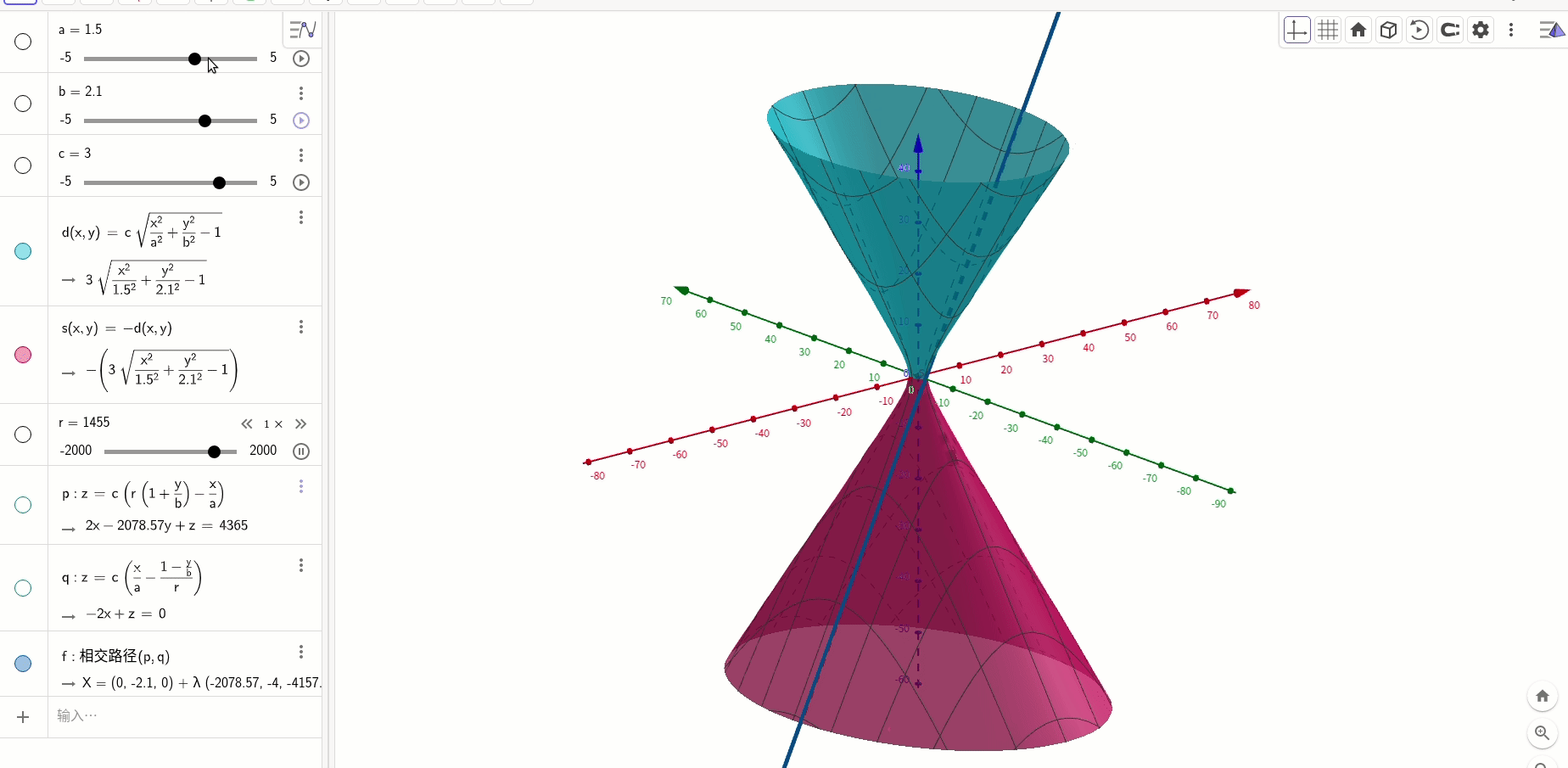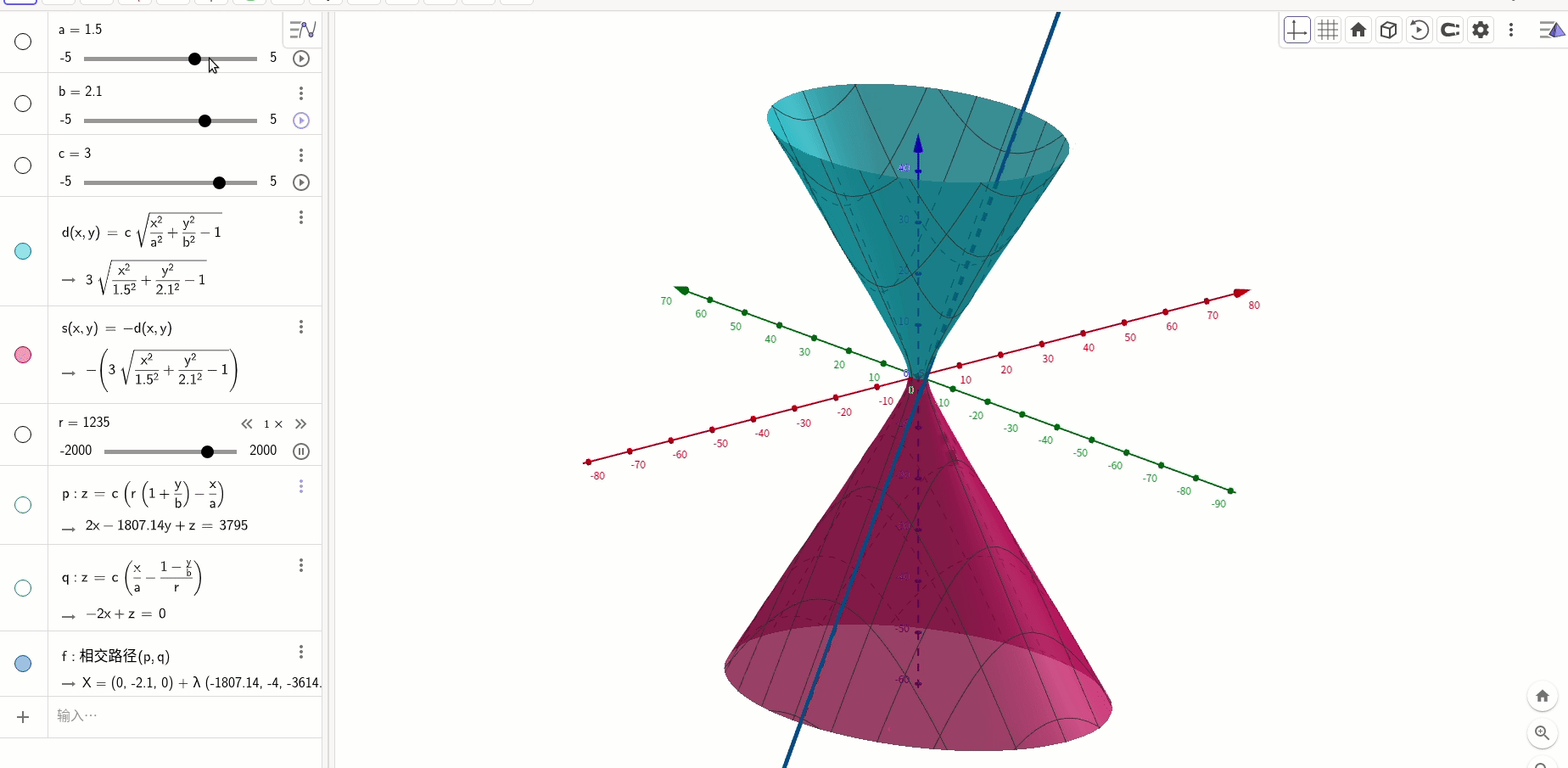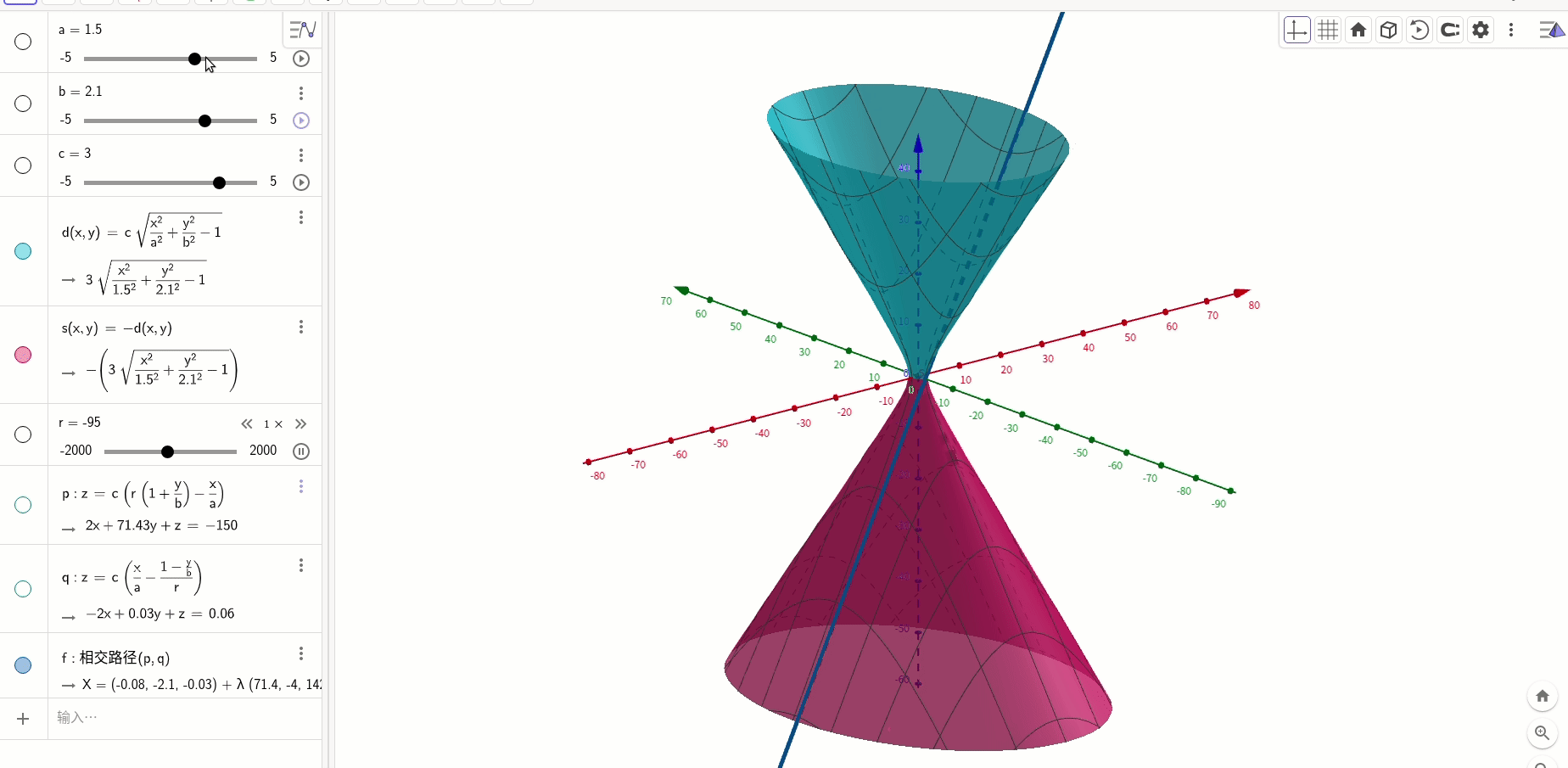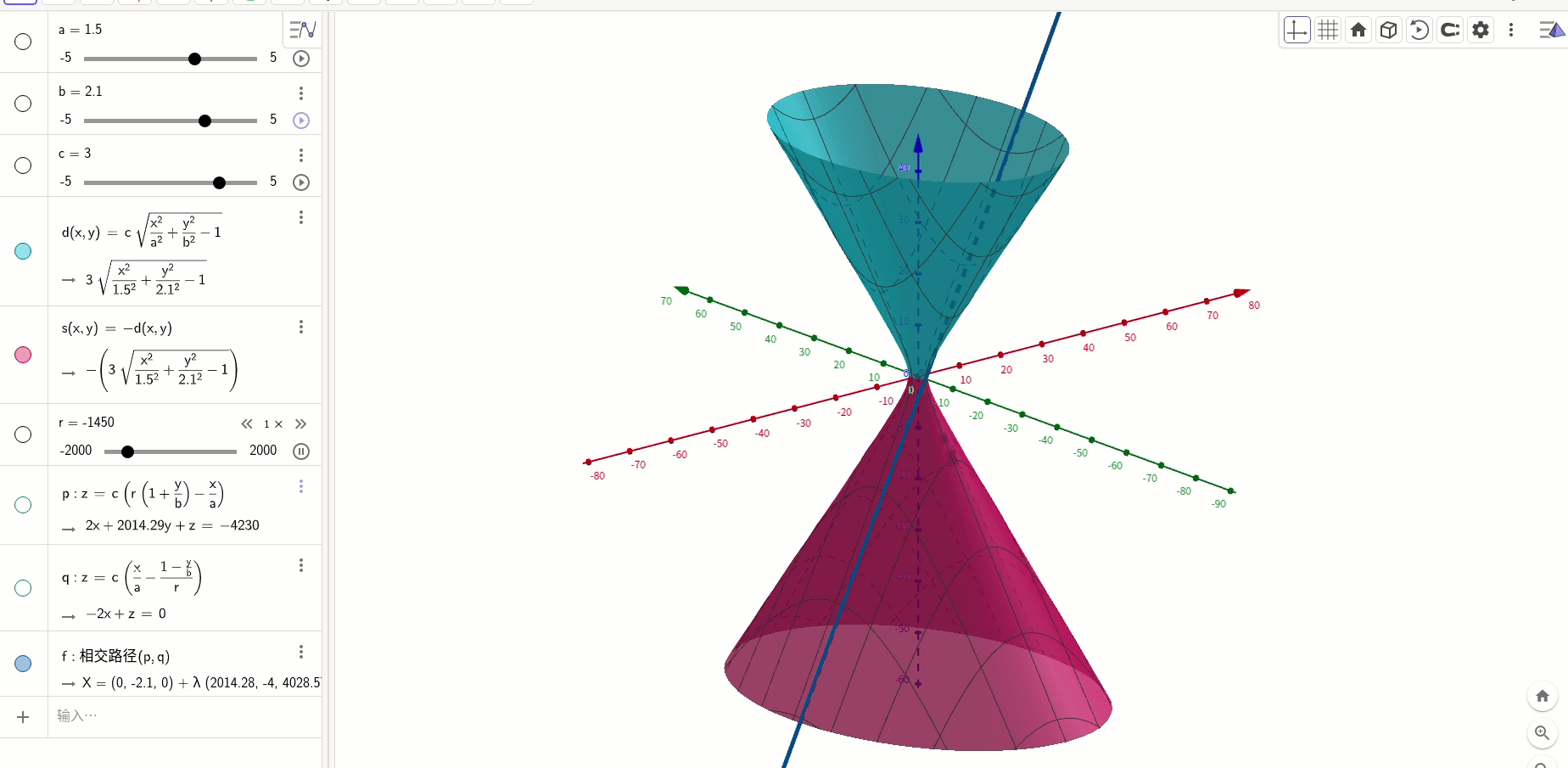
直纹面方程：

直纹面（单叶双曲面）的方程通项公式为：

$\frac{x^2}{a^2}+\frac{y^2}{b^2}-\frac{z^2}{c^2}=1$

绘制出来是这个样子：

和直线的关系，对式子进行变形：

$\frac{x^2}{a^2}-\frac{z^2}{c^2}=1-\frac{y^2}{b^2}$

$(\frac{x}{a}+\frac{z}{c})(\frac{x}{a}-\frac{z}{c})=(1+\frac{y}{b})(1-\frac{y}{b})$

$\frac{\frac{x}{a}+\frac{z}{c}}{1+\frac{y}{b}}=\frac{1-\frac{y}{b}}{ \frac{x}{a}-\frac{z}{c}}=\lambda$

所以，可以分解为两个一次曲面：

$\left\{\begin{matrix} \frac{x}{a}+\frac{z}{c} = \lambda (1+\frac{y}{b})\\ \\ \\ \\ 1-\frac{y}{b}=\lambda(\frac{x}{a}-\frac{z}{c}) \end{matrix}\right.$

一次曲面是平面，两个方程的意思就是两个平面的交线：

3:椭球面

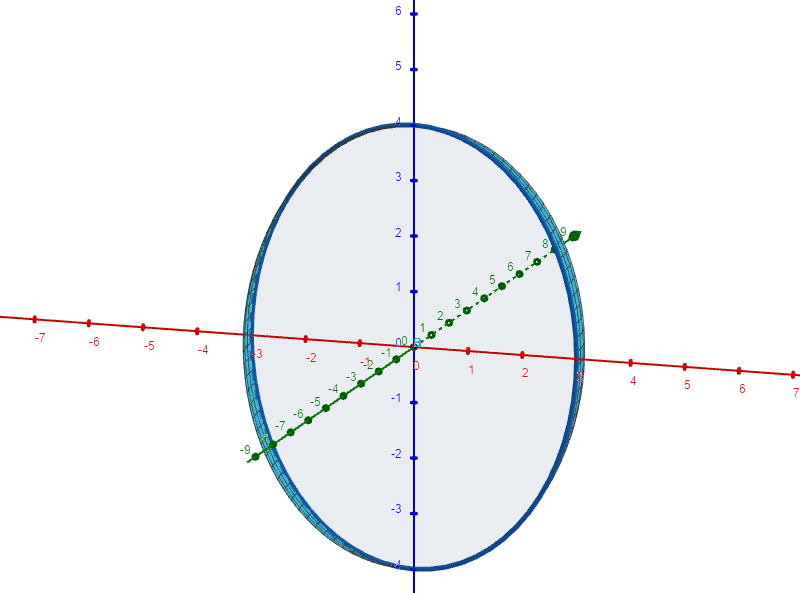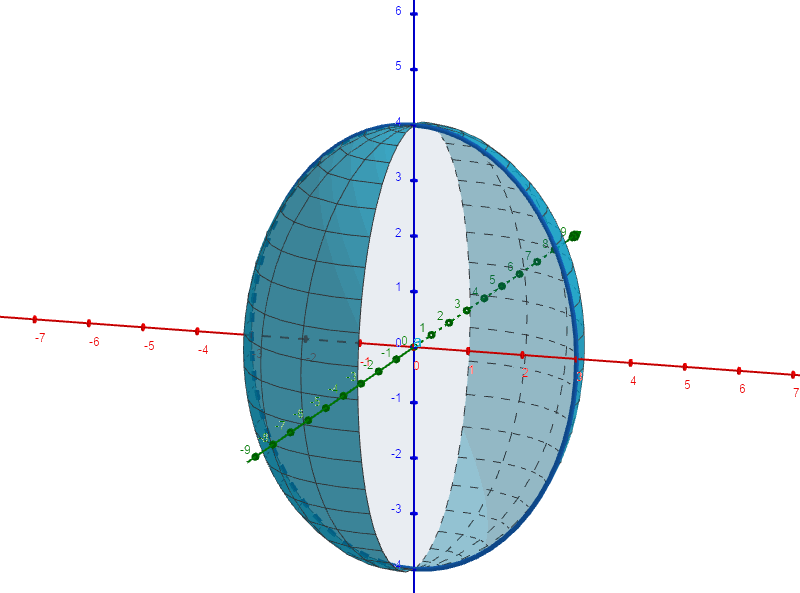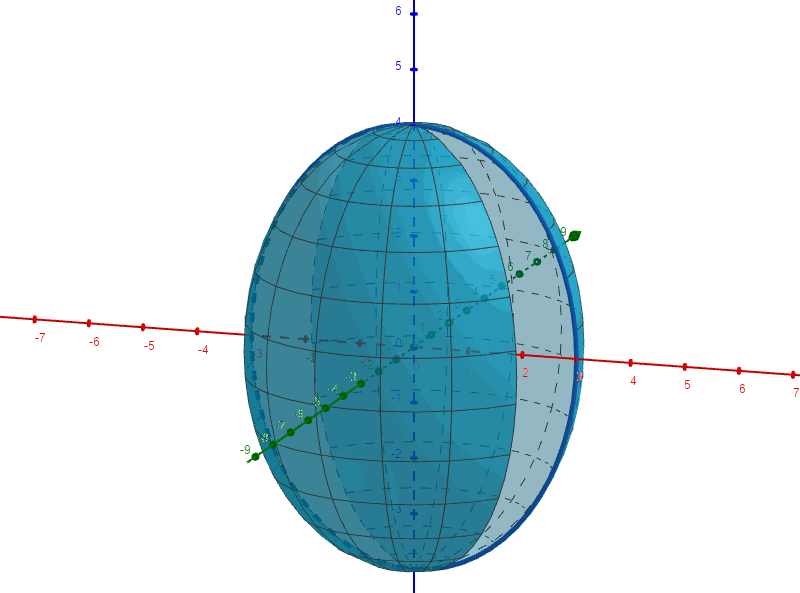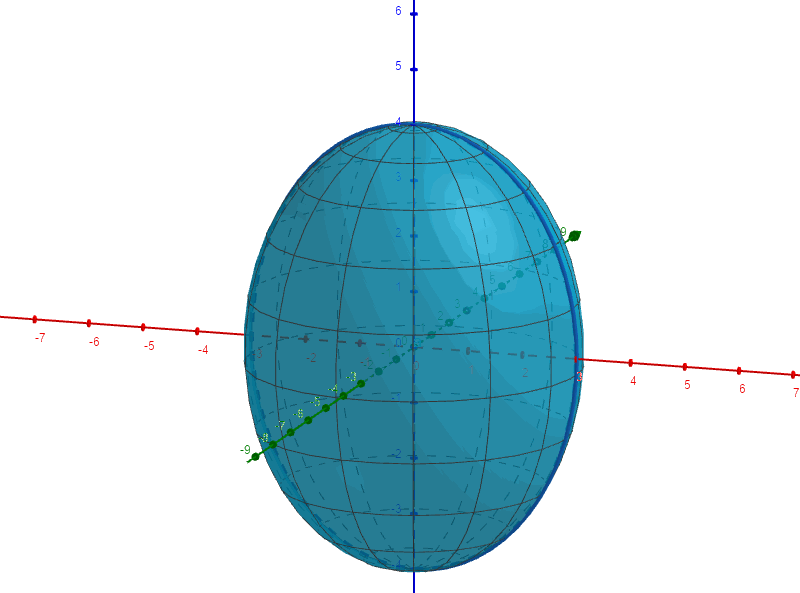
$xOz$ 面上的椭圆

$\frac{x^2}{a^2}+\frac{z^2}{c^2}=1$

绕 $z$ 轴旋转，其方程为：

$\frac{x^2+y^2}{a^2}+\frac{z^2}{c^2}=1$

再把旋转球面沿着y轴方向伸缩

$\frac{b}{a}$

倍，便得到椭球方程

$\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1$

高斯绝妙定理

为什么冷却塔的形状是双曲面？这就和数学家高斯提出的绝妙定理有关了，我们直到，一张纸可以卷成一个圆柱桶，却不可以变成一个球或者半球，这是因为不论纸张还是圆柱体，它的最凸路线和最凹路线的曲率相乘都是0.

$K=k_1\cdot k_2$

这个曲率K就叫做高斯曲率，对于圆通来说，分别为直线和圆，直线的曲率为0,所以高斯曲率为0,而展平的纸张都是直线，高斯曲率也为0.所以，纸张的形态可以在圆柱桶和平面之间变化。

但是对于球面来说，无论怎样，K1,和K2都不为0,它的高斯曲率为正的，一个高斯曲率为0的面是不可能不经过撕裂，压缩而变化的。所以，球的形态比较固定，不会轻易变化。所以高斯曲率不为0的面具有较强的结构强度和抗变形能力，可以有效避免风力影响。而之所以采用双曲面，是因为它是直纹面，以及具有较好的抗压能力，符合混凝土受力特性。