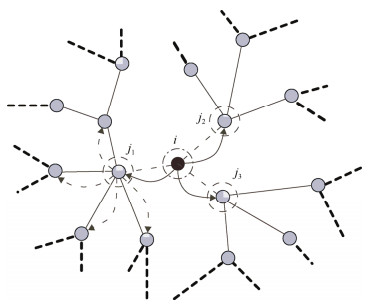
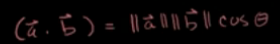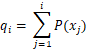三维空间平面拟合MATLAB

article/2025/8/30 12:13:21

1.根据一组点的坐标拟合空间平面，有两种方法：
第一种：如果在测量得到的数据中，x，y值都是确认没有误差的，而误差只是出现在z值上，则可以使用线性回归的方法，此方法最小二乘的目标是在z方向上的残差
Matlab 代码

% 随机生成一组（x,y,z),这些点的坐标离一个空间平面比较近
x0=1,L1=2;
y0=1,L2=2;
x=x0+rand(20,1)*L1;
y=y0+rand(20,1)*L2;
z=1+2*x+3*y;
scatter3(x,y,z,'filled')
hold on;
X = [ones(length(x),1) x y];% 拟合，其实是线性回归，但可以用来拟合平面
% 输出为 b = [b(1) b(2) b(3)] 表示 z = b(1) + b(2)*x + b(3)*y 是拟合出来的平面的方程
[b,bint,r,rint,stats] = regress(z,X,95);% 图形绘制
xfit = min(x):0.1:max(x);
yfit = min(y):0.1:max(y);
[XFIT,YFIT]= meshgrid (xfit,yfit);
ZFIT = b(1) + b(2) * XFIT + b(3) * YFIT;
mesh(XFIT,YFIT,ZFIT);

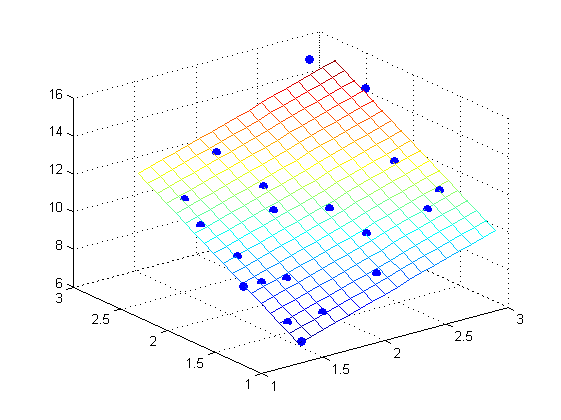
输出结果如图1
在这里插入图片描述
第二中：如果在测量得到的数据中，x，y，z都存在误差，则最小化的目标应该是测量点到平面距离的残差。

% 随机生成一组（x,y,z),这些点的坐标离一个空间平面比较近
x0=1,L1=2;
y0=1,L2=2;
x=x0+rand(20,1)*L1;
y=y0+rand(20,1)*L2;
z=1+2*x+3*y;
scatter3(x,y,z,'filled')
hold on;planeData=[x,y,z];% 协方差矩阵的SVD变换中，最小奇异值对应的奇异向量就是平面的方向
xyz0=mean(planeData,1);
centeredPlane=bsxfun(@minus,planeData,xyz0);
[U,S,V]=svd(centeredPlane);a=V(1,3);
b=V(2,3);
c=V(3,3);
d=-dot([a b c],xyz0);% 图形绘制
xfit = min(x):0.1:max(x);
yfit = min(y):0.1:max(y);
[XFIT,YFIT]= meshgrid (xfit,yfit);
ZFIT = -(d + a * XFIT + b * YFIT)/c;
mesh(XFIT,YFIT,ZFIT);

结果如图2

[参考网址](https://www.ilovematlab.cn/thread-220252-1-1.html) [转](https://blog.csdn.net/shenziheng1/article/details/51175383) [转](https://blog.csdn.net/eric_e/article/details/80983067?utm_source=blogxgwz6)