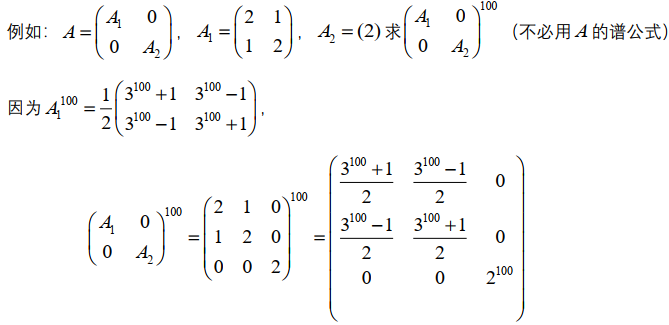内容为个人理解，才疏学浅，如有错误，欢迎指正。

谱分解定理：向量空间V上的任意正规算子M，在V的某个标准正交基下可以对角化。反之，任意可对角化的算子都是正规的。

理解：

（1）一个算子是正规算子当且仅当它可对角化；

（2）算子的可对角化形式是在标准正交向量基下的展开，算子的可对角化有多种形式。谱分解是在A的标准正交化的特征向量基下展开的，谱分解形式只有一种，如果对谱分解形式作用U变换，得到的是A的可对角化形式。

可对角化形式：

谱分解形式：

其中是算子A的特征值，是一组标准正交向量基，是一组标准正交的特征向量基。

我们都学习过线性代数，在相似矩阵那一章节有这样一个概念：

设A,B都是n阶矩阵，其中B是对角阵，若有可逆矩阵P使得,那么我们称矩阵A相似于矩阵B（A和B相似，特征值相同）。假设存在一组U变换，使得：

 P的形式不是唯一的，可利用酉变换改变P，映射到量子中，相当于利用酉变换实现了一组基向另一组基的变化，我们得到了一组新的标准正交向量基，但并不改变A的特征值，因为酉变换是保迹量子运算。