java数据结构-栈

article/2025/8/16 9:02:10

栈

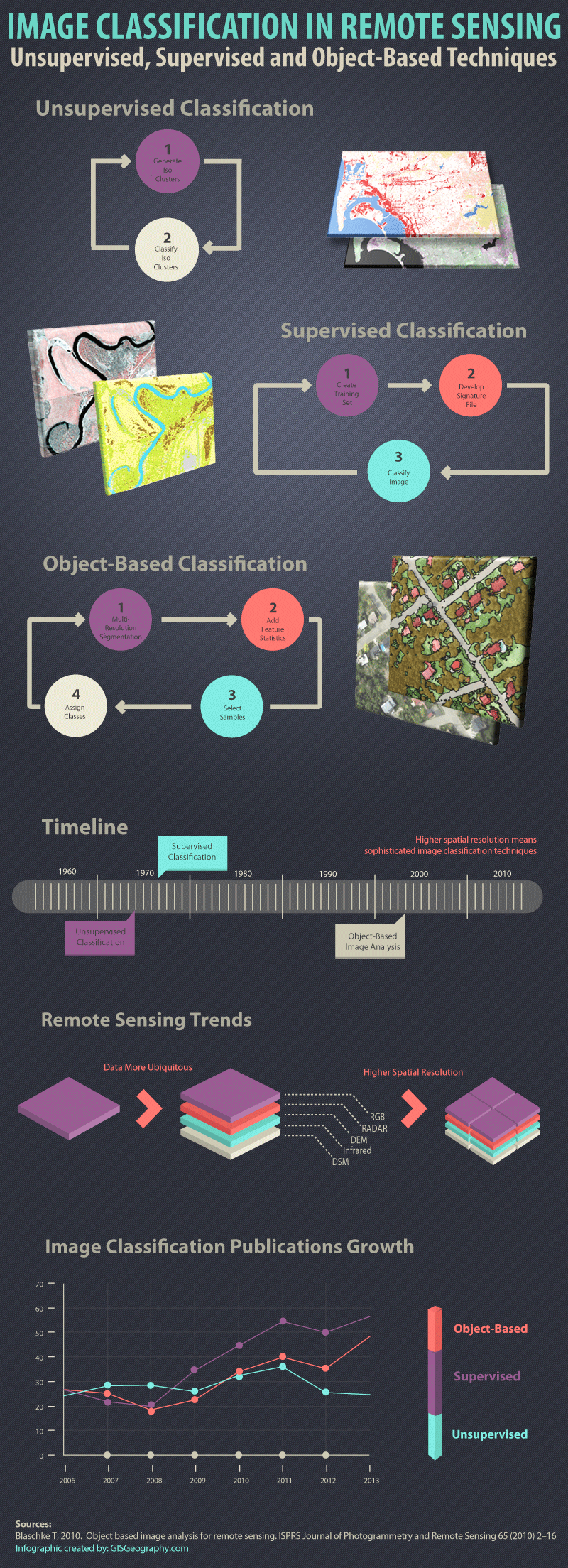
1、栈的定义

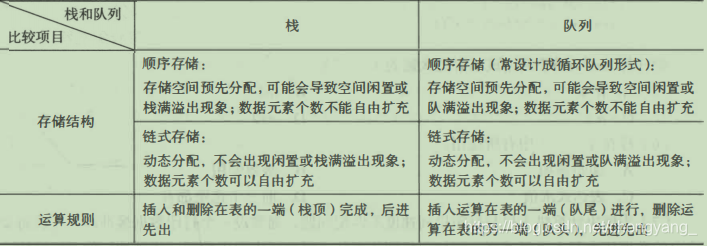
栈（Stack）：是只允许在一端进行插入或删除的线性表。首先栈是一种线性表，但限定这种线性表只能在某一端进行插入和删除操作。

在这里插入图片描述

栈顶（Top）：线性表允许进行插入删除的那一端。
栈底（Bottom）：固定的，不允许进行插入和删除的另一端。
空栈：不含任何元素的空表。

栈又称为后进先出（Last In First Out）的线性表，简称LIFO结构

2、栈的常见基本操作

  • InitStack(&S)：初始化一个空栈S。
  • StackEmpty(S)：判断一个栈是否为空，若栈为空则返回true，否则返回false。
  • Push(&S, x)：进栈（栈的插入操作），若栈S未满，则将x加入使之成为新栈顶。
  • Pop(&S, &x)：出栈（栈的删除操作），若栈S非空，则弹出栈顶元素，并用x返回。
  • GetTop(S, &x)：读栈顶元素，若栈S非空，则用x返回栈顶元素。
  • DestroyStack(&S)：栈销毁，并释放S占用的存储空间（“&”表示引用调用）

3、栈的应用场景

1)子程序的调用：在跳往子程序前，会先将下个指令的地址存到堆栈中，直到子程序执行完后再将地址取出，以回到原来的程序中。

2)处理递归调用：和子程序的调用类似，只是除了储存下一个指令的地址外，也将参数、区域变量等数据存入堆栈中。

3)表达式的转换[中缀表达式转后缀表达式]与求值(实际解决)。

4)二叉树的遍历。

5)图形的深度优先(depth一first)搜索法。

2、栈的基础入门

2.1用数组模拟栈
/*** 使用数组模拟栈* 1.使用数组来模拟栈* 2.定义一个top来表示栈顶,初始化为-1* 3.入栈的操作,当有数据加入到栈时,top++,stack[top] = data；* 4.出栈的操作,int value = stack[top],top--,return value*/
public class Stack {public static void main(String[] args) {ArrayStack stack = new ArrayStack(10);stack.push(1);stack.push(2);stack.push(3);stack.push(4);stack.push(5);stack.list();System.out.println("---");//理论上来说应该是4没有了stack.pop();stack.list();}
}class ArrayStack {private int maxSize;//栈的大小private int[] stack;//数组,模拟栈,数据放在该数组private int top = -1;//标记栈的值//构造器public ArrayStack(int maxSize) {this.maxSize = maxSize;this.stack = new int[this.maxSize];}//判断栈满public boolean isFull() {return top == maxSize - 1;}//判断栈空public boolean isEmpty() {return top == -1;}//入栈-pushpublic void push(int i) {if (isFull()) {System.out.println("栈满");return;}top++;stack[top] = i;}//出栈-poppublic int pop() {if (isEmpty()) {throw new RuntimeException("栈空");}return stack[top--];}//遍历栈[需要从栈顶开始显示数据]public void list() {if (isEmpty()) {System.out.println("栈空没有数据");return;}//如果从栈顶开始显示数据for (int i = top; i >= 0; i--) {System.out.printf("stack[%d]=%d\n",i,stack[i]);}}
}
2.2用链表模拟栈
public class LinkStack {public static void main(String[] args) {Node a1 = new Node(1);Node a2 = new Node(2);Node a3 = new Node(3);LinkStackList ll = new LinkStackList(5);ll.push(a1);ll.push(a2);ll.push(a3);Node pop = ll.pop();System.out.println(pop);ll.list();}}class LinkStackList {private int maxSize;//栈的大小private Node head = new Node(0);//数组,模拟栈,数据放在该头节点private int top = -1;//标记栈的值private Node tmp;public LinkStackList(int maxSize) {this.maxSize = maxSize;}//判断栈空public boolean isEmpty() {return top == -1;}//判断栈满public boolean isFull() {return top == maxSize - 1;}//入栈-pushpublic void push(Node node) {if (isFull()) {System.out.println("栈满");return;}top++;tmp = head;while (true) {if (tmp.next == null) {break;}tmp = tmp.next;}tmp.next = node;tmp = tmp.next;}//出栈-poppublic Node pop() {if (isEmpty()) {System.out.println("栈空");return null;}top--;Node node;node = tmp;tmp = head;while (true) {if (tmp.next.next == null) {tmp.next = null;break;}tmp = tmp.next;}return node;}//    展示public void list() {tmp = head.next;while (tmp != null) {System.out.println(tmp);tmp = tmp.next;}}
}class Node {public int id;public Node next;public Node(int id) {this.id = id;}@Overridepublic String toString() {return "Node{" +"id=" + id +'}';}
}

3、利用栈来实现一个计算器

简单的中缀表达式计算器

请添加图片描述

这是我们的思路分析

public class Calculator {public static void main(String[] args) {String expression = "103+2*6-1";
//        int a = Integer.parseInt(expression);
//        System.out.println(a);//创建两个栈//一个数栈一个符号栈ArrayStack2 numStack = new ArrayStack2(10);ArrayStack2 operStack = new ArrayStack2(10);//定义相关的变量int index = 0;int num1 = 0;int num2 = 0;int oper = 0;int res = 0;char ch = ' ';String keepNum = "";//开始循环的扫描expressionwhile (true) {//依次得到expression 的每一个字符ch = expression.substring(index, index + 1).charAt(0);//开始判断if (operStack.isOper(ch)) {//如果运算符//判断当前符号栈为空if (!operStack.isEmpty()) {//不为空处理//进行比较，如果当前的操作符优先级小于或等于栈中的操作符，就要从数栈中pop出两个数if (operStack.priority(ch) <= operStack.priority(operStack.peek())) {//如果这个元素满足num1 = numStack.pop();num2 = numStack.pop();oper = operStack.pop();res = numStack.cal(num1, num2, oper);//把运算的结果入数栈numStack.push(res);//然后把当前的操作符入符号栈operStack.push(ch);} else {//如果当前的操作符的优先级大于栈中操作符直接入栈operStack.push(ch);}} else {//如果为空直接入栈operStack.push(ch);}} else {//因为0在ascii中是48而不是0
//                numStack.push(ch - 48);//当入数栈的时候不能发现是一个数就立刻入栈,因为他可能是多位数//这样做的话无论多少位也没有关系keepNum += ch;//如果ch已经是最后一位就直接入栈if (index == expression.length() - 1) {numStack.push(Integer.parseInt(keepNum));//重要的!!!keepNum = "";} else {//判断下一个字符表示数组,如果是数字就继续扫描,如果是运算符,则入栈if (operStack.isOper(expression.substring(index + 1, index + 2).charAt(0))) {//如果下一位是运算符则入栈numStack.push(Integer.parseInt(keepNum));//重要的!!!keepNum = "";}}}//让index++,如果字符串没有字符了跳出循环index++;if (index >= expression.length()) {break;}}//当表达式扫描完毕，就顺序从符号栈中去出相应的数和符号,并运行while (true) {//如果符号栈为空则计算到最后了if (operStack.isEmpty()) {break;}//执行最后的运算//如果这个元素满足num1 = numStack.pop();num2 = numStack.pop();oper = operStack.pop();res = numStack.cal(num1, num2, oper);//把运算的结果入数栈numStack.push(res);}int sum = numStack.pop();System.out.println(sum);}
}//先创建一个栈,需要扩展一下功能
class ArrayStack2 {private int maxSize;//栈的大小private int[] stack;//数组,模拟栈,数据放在该数组private int top = -1;//标记栈的值//构造器public ArrayStack2(int maxSize) {this.maxSize = maxSize;this.stack = new int[this.maxSize];}//判断栈满public boolean isFull() {return top == maxSize - 1;}//判断栈空public boolean isEmpty() {return top == -1;}//入栈-pushpublic void push(int i) {if (isFull()) {System.out.println("栈满");return;}top++;stack[top] = i;}//出栈-poppublic int pop() {if (isEmpty()) {throw new RuntimeException("栈空");}return stack[top--];}//展示当前栈顶的元素public int peek() {if (isEmpty()) {throw new RuntimeException("栈空");}return stack[top];}//遍历栈[需要从栈顶开始显示数据]public void list() {if (isEmpty()) {System.out.println("栈空没有数据");return;}//如果从栈顶开始显示数据for (int i = top; i >= 0; i--) {System.out.printf("stack[%d]=%d\n", i, stack[i]);}}//扩展功能:返回运算符的优先级,优先级越高数字越大public int priority(int oper) {if (oper == '*' || oper == '/') {return 1;} else if (oper == '+' || oper == '-') {return 0;} else {return -1; //假设当前的表达式只有加减乘除}}//判断是不是一个运算符public boolean isOper(char val) {return val == '+' || val == '-' || val == '*' || val == '/';}//计算方法public int cal(int num1, int num2, int oper) {int tmp = 0;switch (oper) {case '+':tmp = num1 + num2;break;case '-':tmp = num2 - num1;break;case '*':tmp = num1 * num2;break;case '/':tmp = num2 / num1;break;}return tmp;}
}
后缀表达式计算器

代码

首先我们先需要一个把后缀表达式转换为List的方法

//将逆波兰表达式，依次将数据和运算符放入ArrayList中
public static List<String> getListString(String suffixExpression) {//将suffixExpressionString[] split = suffixExpression.split(" ");List<String> list = new ArrayList<String>();for (String ele : split) {list.add(ele);}return list;
}

然后就是我们真正的计算方法

//完成对逆波兰表达式的运算
//这次我们使用系统提供的栈
public static int calculate(List<String> ls) {//创建一个栈,只需要一个栈就okStack<String> stringStack = new Stack<String>();//遍历lsfor (String item : ls) {//这里使用正则表达式if (item.matches("\\d+")) {//匹配的是多位数//入栈stringStack.push(item);} else {//pop出两个数,并运算,再入栈int num2 = Integer.parseInt(stringStack.pop());int num1 = Integer.parseInt(stringStack.pop());int res = 0;if (item.equals("+")) {res = num1 + num2;} else if (item.equals("-")) {res = num1 - num2;} else if (item.equals("*")) {res = num1 * num2;} else if (item.equals("/")) {res = num1 / num2;} else {throw new RuntimeException("运算符有误");}//把res入栈，把整数转换位字符串stringStack.push(res + "");}}//最后留着栈的元素是运算结果return Integer.parseInt(stringStack.pop());
}
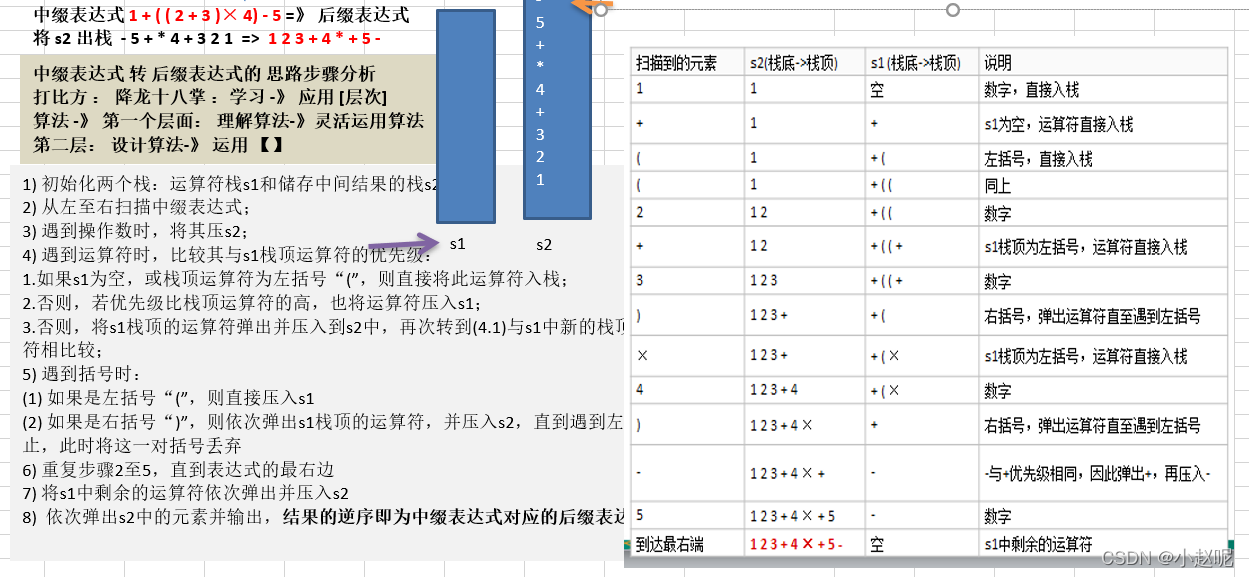
中缀表达式转后缀表达式
String expression = "1+((2+3)*4)-5";

现在我们的需求是把他转换为后缀表达式的list

思路分析
请添加图片描述

代码

首先要先将中缀表达式转换为对应的list

//将中缀转换为对应的list
public static List<String> getInfixListString(String s) {//定义一个List,存放对应的内容List<String> ls = new ArrayList<String>();int i = 0; //这是一个指针,用于遍历sString str;//做多位数拼接char c;//用于存放到cdo {//如果c是一个非数字,我们就需要加入到ls中去if ((c = s.charAt(i)) < 48 || (c = s.charAt(i)) > 57) {ls.add("" + c);i++;//i需要后移} else {//如果是一个数,需要考虑多位数的问题str = "";//先至空while (i < s.length() && (c = s.charAt(i)) >= 48 && (c = s.charAt(i)) <= 57) {str += c;//拼接字符串i++;}ls.add(str);}} while (i < s.length());return ls;
}

把中缀list转换为后缀

//将中缀表达式转换为对应的后缀表达式对应的List
public static List<String> parseSuffixExpressionList(List<String> ls){//定义1个栈Stack<String> s1 = new Stack<String>();//符号栈//定义一个链表List<String> s2 = new ArrayList<String>();//遍历lsfor(String str : ls){//如果是一个数加入s2if(str.matches("\\d+")){s2.add(str);}else if (str.equals("(")) {s1.push(str);}else if (str.equals(")")) {//如果是右括号，依次弹出s1栈顶的运算符，压入s2，直到左括号为止，此时这对括号丢弃while (!s1.peek().equals("(")){s2.add(s1.pop());}s1.pop();//!!!将(弹出小括号} else {//这个就是判断的来的是运算符的情况//当str的优先级小于等于栈顶的优先级//问题我们缺失一个优先级方法//来一个循环不停的对比来的运算符和s1栈顶的运算符优先级while (s1.size() != 0 && Operation.getPriority(s1.peek()) >= Operation.getPriority(str)){s2.add(s1.pop());}//还需要将str压入栈s1.push(str);}}//将s1剩余的运算符依次加入s2while (s1.size() != 0){s2.add(s1.pop());}return s2;//因为是存放到List因此顺序输出就是对应的逆波兰表达式
}

辅助类

帮助我们判断运算符的优先级

class Operation {private static int ADD = 1;private static int SUB = 1;private static int MUL = 1;private static int DIV = 1;//写一个方法，返回对应的优先级public static int getPriority(String operation){int res = 0;switch (operation) {case "+":res = ADD;break;case "-":res = SUB;break;case "*":res = MUL;break;case "/":res = DIV;break;default :break;}return res;}
}int SUB = 1;private static int MUL = 1;private static int DIV = 1;//写一个方法，返回对应的优先级public static int getPriority(String operation){int res = 0;switch (operation) {case "+":res = ADD;break;case "-":res = SUB;break;case "*":res = MUL;break;case "/":res = DIV;break;default :break;}return res;}
}

http://chatgpt.dhexx.cn/article/XwvP5N01.shtml

相关文章

数据结构栈（顺序栈、链栈、插入push、删除pop）、队（循环队，链队、入队push，出队pop）知识点梳理

数据结构栈（顺序栈、链栈、插入push、删除pop）、队（循环队，链队、入队push，出队pop）知识点梳理

数据结构栈知识点梳理 一 栈的定义 栈&#xff08;stack&#xff09;是限定仅在表尾进行插入和删除操作的线性表 不含任何元素的栈称为空栈 允许插入和删除的一端成为栈顶&#xff08;top&#xff09;&#xff0c;另一端称为栈底&#xff08;bottom&#xff09; 具有LIFO&a…
阅读更多...
数据结构栈和队列

数据结构栈和队列

整本书的知识点&#xff0c;点击右方链接&#xff1a;整本书笔记知识点 文章目录 三、栈和队列3.1、栈和队列的定义和特点3.1.1、栈的定义和特点3.1.2、队列的定义和特点 3.2、案例引入3.3、栈的表示和操作的实现3.3.1、栈的类型定义3.3.2、顺序栈的表示和实现3.3.3、链栈的表示…
阅读更多...
C++数据结构——栈

C++数据结构——栈

C数据结构——栈 最近计划再复习一遍数据结构&#xff0c;看到一篇博客&#xff1a;https://www.cnblogs.com/QG-whz/p/5170418.html#_label0。 1、栈(Stack)是一种线性存储结构&#xff0c;它具有如下特点&#xff1a; &#xff08;1&#xff09;栈中的数据元素遵守“先进后…
阅读更多...
数据结构 栈-链栈及基本操作

数据结构 栈-链栈及基本操作

目录 一.栈的定义二.栈的特点三.栈的理解四.链栈引入五.链栈定义六.链栈的结构体设计七.链栈的基本操作7.1链栈的初始化7.2链栈判空7.3链栈入栈7.4链栈出栈7.4取栈顶元素 八.总结 一.栈的定义 栈是限定仅在表尾进行插入和删除操作的数据结构&#xff08;受到限制的线性表&…
阅读更多...
数据结构之——栈

数据结构之——栈

文章目录 数据结构之——栈一&#xff1a;栈的定义&#xff1a;二&#xff1a;栈的抽象数据类型&#xff1a;三&#xff1a;栈的顺序存储结构及其实现&#xff1a;1: 预说明&#xff1a;2&#xff1a;栈的顺序存储结构——结构定义&#xff1a;3:栈的顺序存储结构——进栈操作4…
阅读更多...
数据结构与算法（3）栈

数据结构与算法（3）栈

栈 1、栈的一个实际需求 请输入一个表达式&#xff1a;7x2x2-51-53-3 2、栈的介绍 栈的英文为stack 栈是一个**先入后出(FILO-First In Last Out) **的有序列表 栈(stack) 是限制线性表中元素的插入和删除只能在线性表的同一端进行的一种特殊线性表。 允许插入和删除的一端…
阅读更多...
【数据结构】栈

【数据结构】栈

栈的概念及结构 在学习栈前&#xff0c;我们先看一下栈的正式解释&#xff1a; 栈&#xff1a;一种特殊的线性表&#xff0c;其只允许在固定的一端进行插入和删除元素操作。 进行数据插入和删除操作的一端 称为栈顶&#xff0c;另一端称为栈底。 栈中的数据元素遵守后进先出 L…
阅读更多...
什么是栈？

什么是栈？

本文将介绍一个重要的数据结构—栈&#xff0c;和之前讲到的链表、数组一样也是一种数据呈线性排列的数据结构&#xff0c;不过在这种结构中&#xff0c;我们只能访问最新添加的数据。栈就像是一摞书&#xff0c;拿到新书时我们会把它放在书堆的最上面&#xff0c;取书时也只能…
阅读更多...
【图解数据结构】栈全面总结

【图解数据结构】栈全面总结

目录 一、前言 二、基本概念 三、栈的表示和实现 1.顺序栈 2.链栈 四、栈的常见算法实现 1.初始化 2.判空 3.判满 4.顺序栈取栈顶元素 5.顺序栈入栈 6.顺序栈出栈 五、双栈 1.双端顺序栈进栈操作 2.双端顺序栈出栈操作 六、栈的应用举例 1.回文游戏 2.多进制…
阅读更多...
数据结构——栈

数据结构——栈

栈和队列 栈和队列介绍特点栈、队列与一般线性表的区别栈——stack栈的基本运算栈的存储结构顺序栈链栈 栈的应用 栈和队列 介绍 栈和队列是在软件设计中常用的两种数据结构&#xff0c;它们的逻辑结构和线性表相同 特点 栈和队列在运算上受到了限制&#xff1a;栈是按照“…
阅读更多...
遥感影像百分比线性拉伸

遥感影像百分比线性拉伸

AI Earth地球科学云平台开发者模式提供了丰富的遥感数据和函数计算能力&#xff0c;下面介绍结合AIE Notebook&#xff0c;实现遥感数据的百分比线性灰度拉伸。 本期开发者实践案例——遥感影像百分比线性拉伸 灰度拉伸 (GrayScale Stretch) 是遥感影像处理过程中的重要步骤&…
阅读更多...
遥感影像分类方法

遥感影像分类方法

最初的遥感影像分类是通过目视解译(濮静娟, 1984)来完成的&#xff0c;对研究人员的主观意识有较强的依赖性&#xff0c;而且效率较低&#xff0c;适用于数据量较小的情况&#xff0c;通常作为其他方法对比的对象。目前的遥感图像分类主要以计算机分类为主&#xff0c;因此按照…
阅读更多...
遥感影像配准

遥感影像配准

文章目录 前言步骤1.ENVI&#xff1a;打开Image Registration Workflow2.Image Registration Workflow(1)选择GF2为Base Image File&#xff0c;某季节Sentinel2为Warp&#xff0c;然后Next(2)修改该参数为100(3)人为选择5个左右控制点&#xff0c;然后Next(4)删除离谱点(5)在E…
阅读更多...
遥感图像分类技术

遥感图像分类技术

什么是遥感图像分类技术&#xff1f; 图像分类是将土地覆盖类别分配给像素的过程。例如&#xff0c;这9个全球土地覆盖数据集将图像分为森林、城市、农业和其他类别。 https://gisgeography.com/free-global-land-cover-land-use-data/ 一般来说&#xff0c;这是遥感中的三种主…
阅读更多...
遥感图像分类

遥感图像分类

遥感图像分类 一、背景简介 遥感图像分类就是利用计算机通过对遥感图像中各类地物的光谱信息和空间信息进行分析&#xff0c;选择特征&#xff0c;将图像中各个像元按照某种规则或算法划分不同的类别&#xff0c;然后获得遥感图像中与实际地物的对应信息&#xff0c;从而实现…
阅读更多...
WorldView卫星遥感影像数据/米级分辨率遥感影像

WorldView卫星遥感影像数据/米级分辨率遥感影像

数据样例&#xff1a;百度云下载链接&#xff1a;https://pan.baidu.com/s/17ofPwpDM3OCHnE-LuhvUp 提取码&#xff1a;i0m4 目前世界上最常用的高分辨率卫星影像莫过于WORLDVIEW系列了&#xff0c;在卫星遥感圈内可谓大名鼎鼎&#xff0c;不仅具有超高的分辨率还具有其他高分…
阅读更多...
遥感数据下载平台汇总

遥感数据下载平台汇总

1中国资源卫星应用中心http://www.cresda.com.cn中巴卫星、HJ星、ZY系列 、GF系列2中科院对地观测与数字地球科学中心http://ids.ceode.ac.cn/Index.aspxERS卫星&#xff0c;Enviset_1卫星&#xff0c;法国的spot4卫星&#xff0c;中巴资源卫星&#xff0c;landset-5-73地球系统…
阅读更多...
遥感多光谱数据下载与预处理(一、数据选择 下载)

遥感多光谱数据下载与预处理(一、数据选择 下载)

首先说明本人并非专业大牛&#xff0c;不是教程贴只是记录一下学习过程和大家交流&#xff0c;过程有不严谨不合规范不对的地方欢迎各位大神指正。 本人目前做过接触过最多的是多光谱遥感数据&#xff0c;也是与无人机、雷达、高光谱等相比最简单的一种&#xff0c;这是我自己总…
阅读更多...
地理空间数据云下载遥感影像

地理空间数据云下载遥感影像

目录 1、先上网址&#xff1a;www.gscloud.cn 2、介绍界面&#xff1a; 2.1 “数据资源” 2.2 “高级检索” 1、先上网址&#xff1a;www.gscloud.cn 2、介绍界面&#xff1a; 地理空间数据云&#xff0c;作为国内免费下载遥感卫星影像的一个大平台&#xff0c;随着年代发…
阅读更多...
遥感图像入门

遥感图像入门

遥感图像入门 一、 遥感基本概念地物光谱特性3S 技术瑞利散射大气窗口 二、 遥感系统的组成三、 遥感分类四、 遥感数字图像处理图像与数字图像数字图像获取时的基本参数数字图像类型 一、 遥感基本概念 遥感(Remote Sensing)——遥远的感知&#xff0c;在未接触物体的情况下获…
阅读更多...
推荐文章

Copyright @ 2022~2023