Node2Vec

论文名称：node2vec: Scalable Feature Learning for Networks

论文地址：https://www.kdd.org/kdd2016/papers/files/rfp0218-groverA.pdf

Node2Vec是用于学习网络节点的连续特征表示。node2vec将节点映射为低维特征表示，最大化网络邻居节点的似然表示。定义一组弹性的邻居节点的概念，设计有偏的随机游走策略，学习探索各种各样的邻居表示。

1.FEATURE LEARNING FRAMEWORK

$G = (V, E)$ 表示网络，我们分析方法适用于有向（无向），有权（无权）的网络模型。 $f:V\rightarrow \mathbb{R}^d$ 将节点映射为特征表示，用于下游的预测任务。 $d$ 表示特征表示的维度。 $f$ 是大小为 $|V|\times d$ 的参数矩阵。对于每个source node $\in V$ , 我们定义 $N_{S}(u) \subset V$ 为通过采样策略 $S$ 获得 $u$ 节点的邻居节点。

我们采用扩展的Skip-gram结构。给定节点 $u$ 的特征表示，最大化邻居节点的log-probability。 $f$ 表示如下：
$\max _{f} \sum_{u \in V} \log \operatorname{Pr}\left(N_{S}(u) \mid f(u)\right)\tag{1}$
为了使得优化过程易于处理，我们作出两个假设：

条件独立假设. 在给定source node的节点，他们的邻居节点是是独立的。
$\operatorname{Pr}\left(N_{S}(u) \mid f(u)\right)=\prod_{n_{i} \in N_{S}(u)} \operatorname{Pr}\left(n_{i} \mid f(u)\right)$
Symmertry in feature space。 source node和neighborhood在feature space之间的影响是对称。

对source-neighborhood node pair的特征进行softmax dot product操作：
$\operatorname{Pr}\left(n_{i} \mid f(u)\right)=\frac{\exp \left(f\left(n_{i}\right) \cdot f(u)\right)}{\sum_{v \in V} \exp (f(v) \cdot f(u))}$
根据以上假设Eq.1 简化为：
$\max _{f} \sum_{u \in V}\left[-\log Z_{u}+\sum_{n_{i} \in N_{S}(u)} f\left(n_{i}\right) \cdot f(u)\right]\tag{2}$
对于每个节点的partition function， $Z_{u}=\sum_{v \in V} \exp (f(u) \cdot f(v))$ 对于大型网络的计算代价是非常大的，因此，我们采用负采样。采用随机梯度法优化Eq.2中的模型参数。

在文本中，基于连续的文字序列，通过window size定义它们的邻居。在网络中，采用随机策略生成source节点的不同的邻居，他们的邻居节点依赖于抽样策略 $S$ 。

2.node2vec

基于BFS和DFS，我们设计两者之间平滑的抽样策略。

2.1 Random Walks

设随机游走的长度 $l$ , $c_i$ 是游走的第 $i$ 个节点，起始节点 $c_0=u$ 。节点 $c_i$ 通过以下方式产生：
$P\left(c_{i}=x \mid c_{i-1}=v\right)=\left\{\begin{array}{ll} \frac{\pi_{v x}}{Z} & \text { if }(v, x) \in E \\ 0 & \text { otherwise } \end{array}\right.$
$\pi_{vx}$ 是节点v和节点x之间非标准化的转移概率， $Z$ 是用于标准化的常数。

2.2 Search bias $\alpha$

最简单直接的随机游走方式是基于边的权重 $w_{vx}$ 进行下一个节点的抽样。例如： $\pi_{vx}=w_{vx}$ 。（对于无权图 $w_{vx}=1$ ）。但是，这种情况没有考虑到网络的结构，不能进行不同形式邻居节点的探查。BFS和DFS分别适合结构等价和同质的网络的极端采样范式。现实多是两种情况的融合，我们的随机游走对两者作出平衡。

在这里插入图片描述

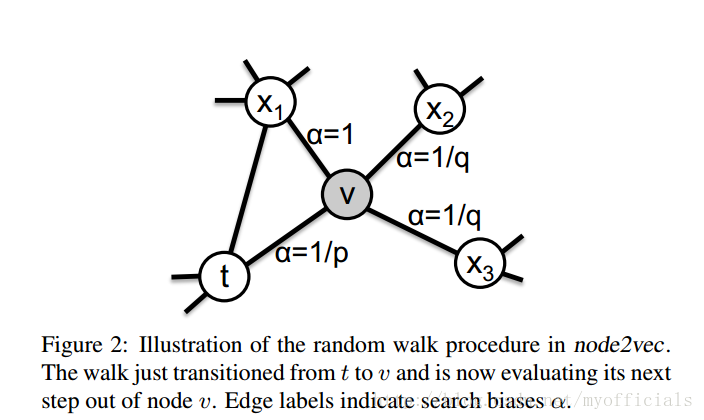
根据 $p$ 和 $q$ 我们定义 $2^{nd}$ 阶的随机游走， $p$ 和 $q$ 引导游走的方式：假设刚游走过一条边 $(t, v)$ , 现在处于节点 $v$ ，（Figure 2）。现在基于边 $(v, x)$ , 决定下一步游走的转移概率 $\pi_{vx}$ 。我们设未标准化的转移概率 $\pi_{vx}=\alpha_{pq}(t,x)\cdot w_{vx}$ ，其中：
$\alpha_{p q}(t, x)=\left\{\begin{array}{ll} \frac{1}{p} & \text { if } d_{t x}=0 \\ 1 & \text { if } d_{t x}=1 \\ \frac{1}{q} & \text { if } d_{t x}=2 \end{array}\right.$
$d_{tx}$ 是节点 $t$ 和节点 $x$ 之间的最短路径。 $d_{tx}$ 是集合 ${0,1,2\}$ 中的一个。两个参数对于引导游走的方式是非常必要的。

直观上，参数 $p$ 和参数 $q$ 是用来控制离开起始节点 $u$ 邻域的速度。特别的，这些参数允许我们的搜索过程在BFS和DFS之间进行插值，从而反映对不同节点的亲和力。

Return parameter $p$

参数 $p$ 控制在游走的过程中，折返（ revisiting）访问节点可能性。如果将其设置一个较高的值 $(\gt \max(q,1))$ ，采样到已经访问过节点的概率是非常小的（除非下一个节点没有邻居节点）。这个策略鼓励新的探索，避免重复过去无效2-hop。另一方面，如果 $p$ 比较小 $(\lt\min(q,1))$ ，它将会导致游走的回溯(Figure 2), 将会导致在节点 $u$ 附近进行local walk。

In-out parameter $q$

参数 $q$ 控制“inward”和“outward”的参数。如Figure 2，如果 $q\gt1$ , 随机游走偏向节点 $t$ 。这个游走获得起始节点的局部视图，类似BFS，获取都是局部样本点。

如果 $q < 1$ , 游走会远离节点 $t$ , 进行更深层次访问。这种行为类似DFS探索。与DFS不同的是，我们基于随机游走的框架实现类似DFS探索。给定样本点 $u$ , 抽样的样本不是严格遵循DFS的distance 递增过程，但是采样的效率是非常高的且易于处理。设 $\pi_{v,x}$ 是在 $t$ 时刻，当前进行节点的函数，它们的随机游走符合马尔科夫性。

Benefits of random walks

在这里插入图片描述

在时间和空间复杂度方面，相对于 BFS和DFS, 随机游走的计算非常高效的。在空间复杂度方面，存储节点邻居 $O ∣ E ∣$ . 在 $2^{nd}$ 随机游走过程中，存储邻居间的交互，它们的空间复杂度是 $O(a^2|V|)$ , 其中 $a$ 是图平均度。在时间复杂度方面，通过在样本生成过程施加图连接，随机游走一种方便的机制，通过跨不同源节点重用样本来提高采样的效率。假设模拟 $l > k$ 随机游走，由于马尔可夫性，我们可以为 $l - k$ 个节点一次产生 $k$ 个样本。因此，每个样本的复杂度为 $O(\frac{l}{k(l-k)})$ 。举例来说，我们随机游走 $l = 6$ , 序列为 ${u, s_4, s_5, s_6, s_8, s_9\}$ , 会产生如下: $N_{S}(u)=\left\{s_{4}, s_{5}, s_{6}\right\}$ ， $N_{S}\left(s_{4}\right)=\left\{s_{5}, s_{6}, s_{8}\right\}$ 和 $N_S(s_5)=\{s_6,s_8,s_9\}$ 。需要注意的是：重用样本在整个过程中会引入偏差，但效率大大提高。

2.3 The node2vec algorithm

在这里插入图片描述

Algorithm 1是node2vec的伪代码，由于起始节点 $u$ 的选择, 在随机游走过程中，会存在隐含的偏差。因为我们要学习所有节点的表示，我们将每个节点作为起始节点，随机游走固定的长度 $l$ , 游走 $r$ 次。每一步的游走基于转移概率 $\pi_{vx}$ 。对于二阶马尔科夫转移概率 $\pi_{vx}$ 可以事先计算。因此，对于节点的采样可以在 $O (1)$ 时间内完成。node2vec可以分为3个阶段：转移概率预计算、随机游走序列生成、SGD优化，三个过程串联进行。每个阶段可以并行、异步执行，对全局进行优化。

3 Learning edge features

node2vec提供半监督的方式学习节点特征表示。然而，相对个体节点，我们通常对节点对的预测任务更加感兴趣。例如，在链路预测任务中，判断两个节点是否存在边。因为随机游走自然地学习到网络节点之间的连接性。我们基于个体节点的特征表示，使用bootstrapping的方法，可以学习节点对之间的关系。

考虑两个节点 $u$ 和 $v$ ，我们基于特征向量 $f (u)$ 和 $f (v)$ 定义二值算子 $\circ$ ，用于计算表征向量 $g (u, v)$ , $\times V \rightarrow \mathbb{R}^{d^{\prime}}$ , 其中， $d^{\prime}$ 是节点对 $(u, v)$ 表征大小。我们想让我们的算子对任何算子定义有效，即使节点之间的边不存在。这样做是方便链路预测。我们的测试数据包含真假边。我们考虑几种算子 $\circ$ , 使得 $d^{\prime}=d$ , 总结在Table 1中。