前言

在KDD 2016 | node2vec：Scalable Feature Learning for Networks
中我们详细讨论了node2vec的机制，但并没有给出代码实现。本篇文章将从原文出发，逐步详细地讨论如何一步步实现node2vec。

1.数据导入

数据为《Les Misérables network》，也就是《悲惨世界》中的人物关系网络：该图是一个无向图，图中共77个节点、254条边。节点表示《悲惨世界》中的人物，两个节点之间的边表示这两个人物出现在书的同一章，边的权重表示两个人物（节点）出现在同一章中的频率。

import networkx as nx
G = nx.les_miserables_graph()

原文中node2vec的算法描述如下：

其中node2vecWalk用于产生一个从节点$u$开始的长为$l$的游走序列，LearningFeatures利用所有节点产生的游走序列来进行word2vec，得到每个节点的向量表示。

下面我将结合原文详细介绍这两个算法！！

2.node2vecWalk

2.1 归一化转移概率

2.1.1 原理解析

node2vecWalk算法的伪代码描述如下：

1. 将初始节点$u$加入到walk中
2. 当前节点curr为walk中最后一个节点
3. 根据curr和其对周围节点的转移概率选择下一个节点$s$，并将其加入walk
4. 当walk长度为$l$时采集结束，返回walk

描述比较模糊，我们再看看原文：

当前节点是$v$，下一个要采集的节点是$x$，则我们有如下概率公式：

可以发现，我们只会采样跟当前节点$v$间有边存在的节点，对于不与当前节点$v$相连的节点，我们不会去采样。

采样概率是一个归一化的转移概率：$\frac{{\pi }_{vx}}{Z}$，原文中${\pi }_{vx}$的描述为：


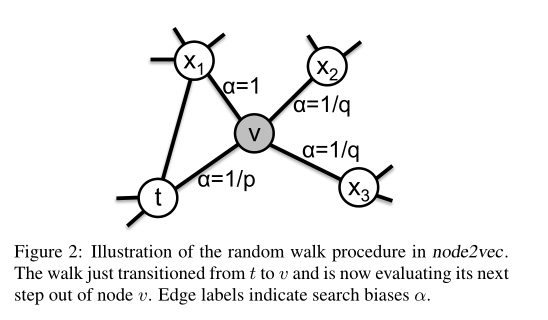
观察上图：节点$t$已经被采样了，紧接着我们采样了节点$v$，现在需要做的是采样$v$之后的下一次采样。根据前文所述，我们只会在节点$v$的邻接节点中选择一个进行采样，也就是在三个$x$中进行采样。这个时候${\pi }_{vx}={\alpha }_{pq}(t,x)\cdot w_{vx}$，其中$w_{vx}$表示两个节点间的权重（如果是无权图，则权重为1）

但是存在一个问题： 如果我们是进行第二次采样（第一次是初始结点$u$），则有$v=u$，$x$表示与$u$相连的节点。这个时候我们就会发现没法利用${\pi }_{vx}={\alpha }_{pq}(t,x)\cdot w_{vx}$来计算两个节点间的转移概率，因为不存在节点$t$，也就没法计算${\alpha }_{pq}(t,x)$！！

解决： 此时的${\pi }_{vx}$就是$w_{vx}$。

因此，第一步的思路就很明确了：

1. 如果当前要进行第二次采样，我们就算出第一个节点$u$到其所有节点的归一化转移概率：非归一化转移概率${\pi }_{vx}$就是节点$u$与其邻接节点相连边的权重（可能不在01间），归一化就是将所有概率变换到01之间：所有概率除以归一化常数$Z$，$Z$为这些权重之和。
2. 否则，我们则根据当前节点$v$和上一个被采样的节点$t$，算出$v$到其所有邻接节点$x$的非归一化转移概率：${\pi }_{vx}={\alpha }_{pq}(t,x)\cdot w_{vx}$，然后同样除以它们的和来进行归一化。

2.1.2 Alias采样

当我们有了当前节点对其所有邻接节点的转移概率后，我们应该怎么选择？是选择一个转移概率最大的节点进行采样吗？

答案显而易见，肯定不是！ 原文中算法描述如下：

可以看到作者采用了一种叫做AliasSample的采样方法，AliasSample，又名“别名采样”，是一种比较经典的采样算法。比如：游戏中经常遇到按一定的掉落概率来随机掉落指定物品的情况，例如掉落银币25%，金币20%, 钻石10%，装备5%，饰品40%。现在要求下一个掉落的物品类型，或者说一个掉落的随机序列，要求符合上述概率。

在本文中可以描述为：我们已经有了待选节点集，也有了选择它们的概率，现在我们要进行下一次选择，要求该选择符合上述概率要求。

在Alias Sample中，我们输入一个概率列表，最后会得到两个数组：Prob和Ailas

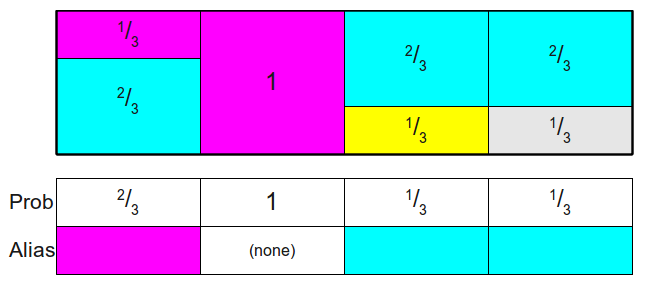
然后：随机取某一列$k$(即[1,4]的随机整数)，再随机产生一个[0-1]的小数$c$，如果$Prob[k]>c$，那么采样结果就是$k$，反之则为Alias[k]。

关于Alias Sample的详细原理可以参考：Alias Sample，这里不再详细介绍。

2.1.3 代码实现

有了以上思路后我们就很容易编写代码了：

1. 对于第一种情况：我们可以初始化一个字典nodes_info，nodes_info[node]表示与node有关的所有信息，其中nodes_info[node][0]和nodes_info[node][1]分别表示输入当前node与其邻接点的转移概率列表后得到的Alias数组和Prob数组。
2. 对于第二种情况，我们可以初始化一个字典edges_info，其中edges_info[(t, v)][0]和edges_info[(t, v)][1]分别表示输入$v$到所有$x$的转移概率列表后得到的Alias数组和Prob数组。

因此，代码实现如下：

def init_transition_prob(self):""":return:归一化转移概率矩阵"""g = self.Gnodes_info, edges_info = {}, {}for node in g.nodes:nbs = sorted(g.neighbors(node)) # 当前节点的邻居节点probs = [g[node][n]['weight'] for n in nbs] # 概率就是权重# 归一化norm = sum(probs)  # 求和normalized_probs = [float(n) / norm for n in probs]  # 归一化nodes_info[node] = self.alias_setup(normalized_probs)  # 利用Alias采样得到Alias和Probfor edge in g.edges:# 有向图if g.is_directed():edges_info[edge] = self.get_alias_edge(edge[0], edge[1])# 无向图else:edges_info[edge] = self.get_alias_edge(edge[0], edge[1])edges_info[(edge[1], edge[0])] = self.get_alias_edge(edge[1], edge[0])self.nodes_info = nodes_infoself.edges_info = edges_info

其中alias_setup函数就是Alias Sample的具体实现，代码直接参考了网上现成的：

def alias_setup(self, probs):""":probs: v到所有x的概率:return: Alias数组与Prob数组"""K = len(probs)q = np.zeros(K)  # 对应Prob数组J = np.zeros(K, dtype=np.int)  # 对应Alias数组# Sort the data into the outcomes with probabilities# that are larger and smaller than 1/K.smaller = []  # 存储比1小的列larger = []  # 存储比1大的列for kk, prob in enumerate(probs):q[kk] = K * prob  # 概率if q[kk] < 1.0:smaller.append(kk)else:larger.append(kk)# Loop though and create little binary mixtures that# appropriately allocate the larger outcomes over the# overall uniform mixture.# 通过拼凑，将各个类别都凑为1while len(smaller) > 0 and len(larger) > 0:small = smaller.pop()large = larger.pop()J[small] = large  # 填充Alias数组q[large] = q[large] - (1.0 - q[small])  # 将大的分到小的上if q[large] < 1.0:smaller.append(large)else:larger.append(large)return J, q

对于不是第二次采样的情况，需要利用get_alias_edge来得到一条边$(t,v)$中$v$到其邻居节点转移概率的Alias数组和Prob数组：

def get_alias_edge(self, t, v):"""Get the alias edge setup lists for a given edge."""g = self.Gp = self.pq = self.qunnormalized_probs = []for v_nbr in sorted(g.neighbors(v)):if v_nbr == t:unnormalized_probs.append(g[v][v_nbr]['weight'] / p)elif g.has_edge(v_nbr, t):unnormalized_probs.append(g[v][v_nbr]['weight'])else:unnormalized_probs.append(g[v][v_nbr]['weight'] / q)norm_const = sum(unnormalized_probs)normalized_probs = [float(u_prob) / norm_const for u_prob in unnormalized_probs]return self.alias_setup(normalized_probs)

代码很容易理解：考虑v的邻居节点v_nbr：如果v_nbr就是t，则非归一化转移概率为$\frac{1}{p}\times w$；如果v_nbr与t间有边，也就是图中$x_1$，则${\alpha }_{pq}(t,x)=1$，即非归一化转移概率为$1\times w$；否则就是图中$x_2,x_3$这种情况，非归一化转移概率为$\frac{1}{q}\times w$。$w$是两个节点间边的权重。

有了非归一化转移概率后，我们再进行归一化（除以和），最后再利用alias_setup函数获得Alias数组和Prob数组。

当我们有了各个节点间的转移概率时，我们在真正采样时需要做出决策，在这些相邻结点中选择一个作为下一个被采样的节点：随机取某一列$k$(即[1,n]的随机整数，n为邻居节点的个数)，再随机产生一个[0-1]的小数$c$，如果$Prob[k]>c$，那么采样结果就是$k$，反之则为Alias[k]。该采样函数实现较为简单：

def alias_draw(self, J, q):"""输入: Prob数组和Alias数组输出: 一次采样结果"""K = len(J)# Draw from the overall uniform mixture.kk = int(np.floor(npr.rand() * K))  # 随机取一列# Draw from the binary mixture, either keeping the# small one, or choosing the associated larger one.if npr.rand() < q[kk]:  # 比较return kkelse:return J[kk]

其中kk或者J[kk]就是我们最终采样的结果。

2.2 node2vecWalk的实现

有了转移概率以及采样策略后，我们就能轻松实现node2vecWalk了：

实现代码如下：

def node2vecWalk(self, u):walk = [u]g = self.Gl = self.lnodes_info, edges_info = self.nodes_info, self.edges_infowhile len(walk) < l:curr = walk[-1]v_curr = sorted(g.neighbors(curr))if len(v_curr) > 0:if len(walk) == 1:walk.append(v_curr[self.alias_draw(nodes_info[curr][0], nodes_info[curr][1])])else:prev = walk[-2]ne = v_curr[self.alias_draw(edges_info[(prev, curr)][0], edges_info[(prev, curr)][1])]walk.append(ne)else:breakreturn walk

下面对重要代码进行解析：

curr = walk[-1]
v_curr = sorted(g.neighbors(curr))

首先得到当前路径中的最后一个节点curr，并得到它的所有邻居节点v_curr。

walk.append(v_curr[self.alias_draw(nodes_info[curr][0], nodes_info[curr][1])])

如果curr的邻居节点不为空且当前walk的长度为1，即我们前面提到的第一种情况：进行第二次采样。那么这个时候我们就需要利用Alias Sample从其所有邻居节点中选择一个节点：nodes_info[curr][0]和nodes_info[curr][1]分别代表Alias数组和Prob数组。

prev = walk[-2]
ne = v_curr[self.alias_draw(edges_info[(prev, curr)][0], edges_info[(prev, curr)][1])]

如果当前不是进行第二次采样，则分别找到$t$和$v$，也就是prev和curr，然后进行Alias Sample。

最终返回的walk即为从$u$开始的一条长为$l$的随机游走路径。

3.LearnFeatures

具体步骤：

1. walks用来存储随机游走，先初始化为空
2. 一共要进行$r$次循环，每一次循环要为图中每个节点都生成一个长度为$l$的游走序列
3. 第iter次循环中对所有节点都利用node2vec算法生成一个随机游走序列walk，然后将其加入walks
4. 得到所有节点的$r$个随机游走序列后，利用SGD方法得到每一个节点的向量表示。

代码实现：

def learning_features(self):g = self.Gwalks = []nodes = list(g.nodes())for iter in range(self.r):np.random.shuffle(nodes)for node in nodes:walk = self.node2vecWalk(node)walks.append(walk)# embeddingwalks = [list(map(str, walk)) for walk in walks]model = Word2Vec(sentences=walks, vector_size=self.d, window=self.k, min_count=0, sg=1, workers=3)f = model.wvreturn f

walks中存储中每一个节点的$r$条长为$l$的随机游走路径，输出前两条：

['MmeBurgon', 'Gavroche', 'Mabeuf', 'Feuilly', 'Gavroche', 'MmeBurgon', 'Gavroche', 'Bossuet', 'Enjolras', 'Feuilly', 'Mabeuf', 'MotherPlutarch', 'Mabeuf', 'Courfeyrac', 'Bossuet', 'Combeferre', 'Courfeyrac', 'Combeferre', 'Bossuet', 'Enjolras', 'Feuilly', 'Enjolras', 'Claquesous', 'Montparnasse', 'Brujon', 'Babet', 'Valjean', 'Toussaint', 'Cosette', 'Valjean', 'Woman1', 'Valjean', 'Cosette', 'Marius', 'Bossuet', 'Combeferre', 'Bahorel', 'Courfeyrac', 'Combeferre', 'Gavroche', 'Bahorel', 'Feuilly', 'Bossuet', 'MmeHucheloup', 'Bossuet', 'Combeferre', 'Courfeyrac', 'Enjolras', 'Valjean', 'Marius', 'Eponine', 'Marius', 'Combeferre', 'Bahorel', 'Courfeyrac', 'Enjolras', 'Valjean', 'Marius', 'Gillenormand', 'MlleGillenormand', 'MmePontmercy', 'MlleGillenormand', 'Gillenormand', 'Cosette', 'Thenardier', 'Brujon', 'Gavroche', 'MmeHucheloup', 'Gavroche', 'Combeferre', 'Feuilly', 'Prouvaire', 'Bossuet', 'Enjolras', 'Valjean', 'Thenardier', 'MmeThenardier', 'Cosette', 'Valjean', 'MmeDeR']
['Feuilly', 'Bossuet', 'Bahorel', 'Prouvaire', 'Enjolras', 'Marius', 'Cosette', 'Javert', 'Valjean', 'Cosette', 'Valjean', 'Marguerite', 'Fantine', 'Dahlia', 'Favourite', 'Listolier', 'Blacheville', 'Fantine', 'Marguerite', 'Fantine', 'Zephine', 'Listolier', 'Tholomyes', 'Blacheville', 'Fameuil', 'Fantine', 'Marguerite', 'Fantine', 'Javert', 'Thenardier', 'Valjean', 'Enjolras', 'Claquesous', 'Thenardier', 'Marius', 'Cosette', 'MlleGillenormand', 'Gillenormand', 'Valjean', 'Thenardier', 'Boulatruelle', 'Thenardier', 'Cosette', 'Marius', 'Eponine', 'Claquesous', 'Javert', 'Valjean', 'Javert', 'Thenardier', 'Javert', 'Enjolras', 'Grantaire', 'Combeferre', 'Gavroche', 'Joly', 'Marius', 'Cosette', 'Valjean', 'Javert', 'Babet', 'Claquesous', 'Enjolras', 'Feuilly', 'Combeferre', 'Bahorel', 'Courfeyrac', 'Enjolras', 'Marius', 'Thenardier', 'Javert', 'Valjean', 'Isabeau', 'Valjean', 'Fauchelevent', 'Gribier', 'Fauchelevent', 'Javert', 'Enjolras', 'Marius']

可以看到第一条随机游走路径是以节点MmeBurgon开始的，第二条是从节点Feuilly开始的，两条路径长度都为$l$。

有了walks之后，我们利用gensim库中的Word2Vec进行训练，进而得到所有节点的向量表示：

model = Word2Vec(sentences=walks, vector_size=self.d, window=self.k, min_count=0, sg=1, workers=3)

其中：

1. sentences是我们要分析的语料，在node2vec中就是随机游走路径的集合。
2. vector_size是节点向量的维度，这里为$d$。
3. window是词向量上下文最大距离，即Skip-Gram和CBOW中窗口的长度，默认值为5。
4. min_cout：可以对字典做截断，词频少于min_count次数的单词会被丢弃掉，默认值为5，这里设置为0。
5. sg：模型选择，sg=1表示采用Skip-Gram模型，sg=0表示采用CBOW模型，默认为0，这里选择Skip-Gram模型。
6. workers：训练并行数，这里选择3。

最终，f中存储着所有节点的长度为$d$的向量表示，任意输出一个：

print(f['MmeBurgon'])

MmeBurgon节点的向量表示为：

[-0.05092877 -0.02686426 -0.2292252   0.11856086  0.02136412  0.01406081-0.26274496 -0.15402426  0.1976506  -0.03906344 -0.1944654   0.03440150.17913733  0.08412573  0.14779484 -0.00783093 -0.17162482 -0.28095236-0.32425568  0.2492605   0.14210573 -0.06607451  0.40488595 -0.15641351-0.01836408  0.0923218  -0.07496541  0.1163046   0.01180712  0.24809936-0.04660206 -0.36390662 -0.20256323 -0.07164664 -0.03223448  0.06946431-0.28120005 -0.14545655  0.2894095  -0.00597684 -0.2806793  -0.025172080.21234442 -0.35515746  0.03860907  0.12777379  0.31198564 -0.04142399-0.06592249 -0.01730651  0.06897946 -0.26776454 -0.00844726 -0.137025740.23738769 -0.23513325  0.05750211  0.01762778 -0.03779545 -0.290608820.1997382   0.012223   -0.23850201 -0.16767174  0.0212742   0.117177730.08926564  0.10213668 -0.07187556 -0.02068917  0.07960241 -0.150149390.1681073   0.12445314  0.13363989 -0.23188415 -0.17411086  0.23457739-0.13661143  0.3249664  -0.07310021  0.24981983 -0.01397824  0.28996238-0.02117981 -0.12742186  0.33266178  0.07946197  0.29308477  0.05445471-0.00712562 -0.06370848  0.16291171 -0.04468412  0.33400518 -0.19028513-0.2808339   0.01152208 -0.13062981 -0.27341706 -0.20656888  0.22132947-0.20722346 -0.05620798 -0.33125588  0.05310262 -0.17866907  0.203493030.09851206  0.03873271 -0.20351988  0.15531495 -0.09796275 -0.20567754-0.16734612  0.04089455  0.22214974  0.29019567 -0.0675301  -0.25800622-0.19473355  0.30337527 -0.3567541   0.11847463  0.00324172 -0.10936202-0.07167141 -0.01137679]

4.参数选择

参数为DeepWalk和LINE的典型值：

返回参数$p$和出入参数$q$的选择：$p=1,q=0.5$

if __name__ == '__main__':p, q = 1, 0.5d, r, l, k = 128, 10, 80, 10G = nx.les_miserables_graph()node2vec = node2vec(G, p, q, d, r, l, k)model = node2vec.learning_features()

5.完整代码

我把数据和代码放在了GitHub上：完整代码，原创不易，下载时请随手给个follow和star，感谢！